1. 极限
简单的极限,我们可以通过直接代入法求解,如:
我们知道我们在利用极限求导数时:
如果直接用代入法的话,会出现分母为0的情况。
2. 连续
连续的定义:
We say f(x) is continuous at x0 when
limx→x0f(x)=f(x0)
四类不连续点
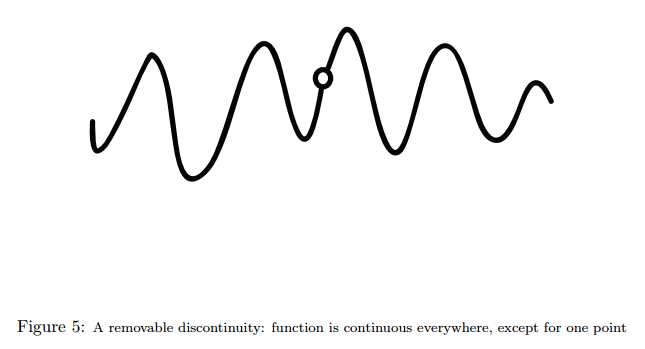
1. Removable Discontinuity
Right-hand limit:
limx→x+0f(x)
means
limx→x0f(x)
for
x>x0
.
Left-hand limit:
limx→x−0f(x)
means
limx→x0f(x)
for
x<x0
.
If limx→x+0f(x)=limx→x−0f(x) but this is not f(x0) , or if f(x0) is undefined, we say the discontinuity is
removable.
比如说 sinxx,x≠0 。
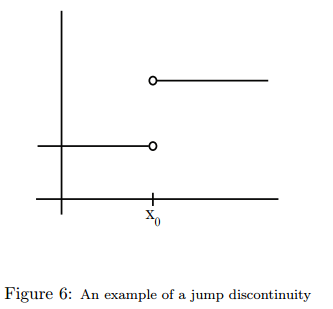
2. Jump Discontinuity
limx→x+0f(x) for( x<x0 ) exists, and limx→x−0f(x) for( x>x0 )also exists, but they are NOT equal.
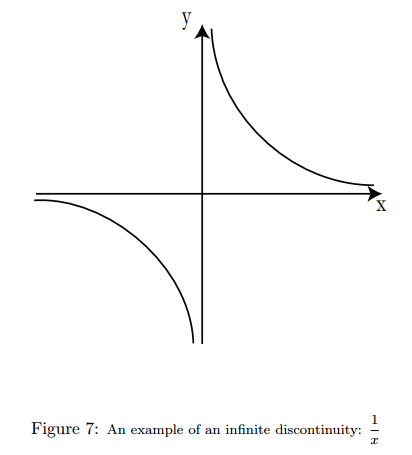
3. Infinite Discontinuity
Right-hand limit:
Left-hand limit:
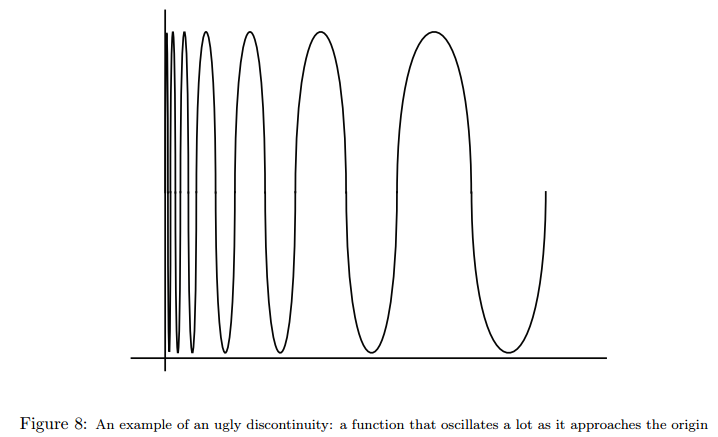
4. Other(Ugly) discontinuity
This function doesn’t even go to ±∞ — it doesn’t make sense to say it goes to anything. For something like this, we say the limit does not exist.
3. 两个三角函数的极限
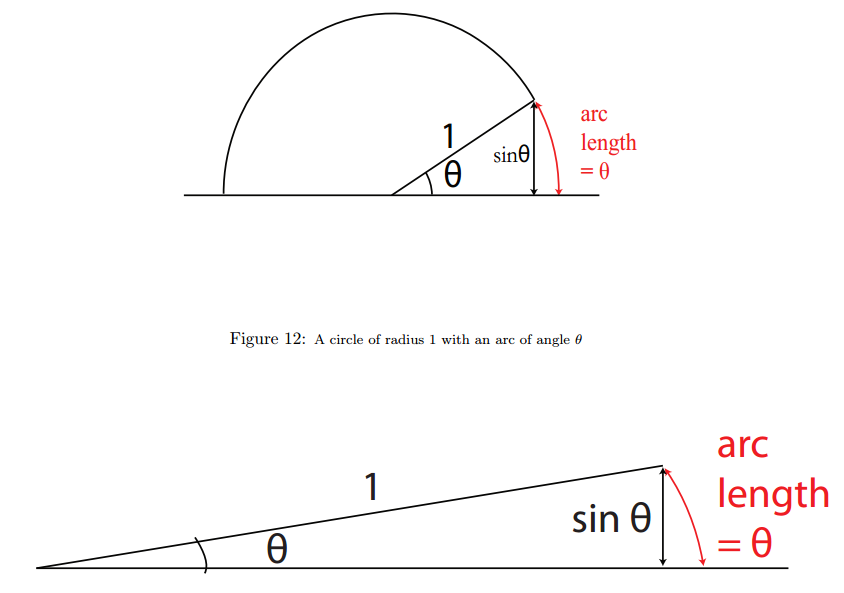
注意下面的表达式中 θ 代表弧度,而不是角度。
几何证明:
当上图中的角度 θ 变得非常小的时候,我们可以看出半弦长( sinθ )越来越接近半弧长( θ )。
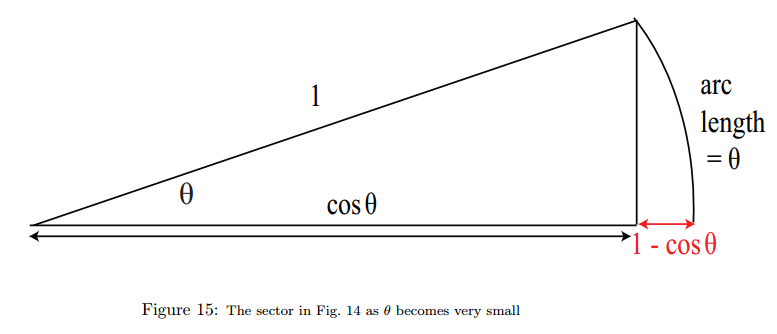
从上图中可以看出当角度变得越来越小时, 1−cosθ 相对于 θ 来显得越来越小。
4. 定理:可微则一定连续
If f is differentiable at
x0 , then f is continuous atx0 .
Proof:





















 8571
8571

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








