联赛联考2

策略总结
这场联考发挥的很糟糕。该拿的分总因为一些失误流失严重。比如说爆类型损失了164分，粗心没看清输出格式少了100分。这些分如果没丢是可以排很前的。
总的来说这次模拟题目整体不难。
Day1
T1怎么看都是水题，一直怀疑有坑，但其实没有。几乎全场都过了。
T2很快想到了可持久化线段树，写完了后对拍，没拍出错，极限数据也很靠谱。
T3时间有点不足，随手写了个spfa转移的dp水个20分。
期望220分。结局100+20+20=140
T2过对拍都错了？！
靠，暴力程序和正解都爆类型了。
现在才知道多项式每一项都要转个类型，以前以为一个转了整条式子会同步转。
好心塞，两个字母带走了80分
Day2
T1题面没说模数是质数，直接放弃，写个15分暴力。
T2题面很高端，似懂非懂，但直觉告诉我找一个环输出可能能水很多分。
T3觉得是规律题，有循环节。先写了个暴力发现了的确有规律，然后按规律写了正解，对拍，拍出错了，发现$m<log_2K$是不符合规律，但仍有循环节，由于m很小，循环节也很小，就机智的写了个hash判循环节。对拍也过了。大数据也貌似没爆。

期望150左右（T2情况不明）
结局15+0+46=61
T2居然正解就是找一个环输出，很多人不明不白的过了。而我由于仓促之中输出了答案序列忘记输出答案序列长度，白白少了100
T3调了半天才发现，又爆类型了，这次是另外一种爆类型 1<< p 即使你的p是$longlong$,也会爆，要把1也转类型才没问题。

连续两天爆类型，心好累。

D2T1由于出题人疏忽忘记说了p是质数，但p是合数也可以做。

题面 ：
$Ans = \Sigma_{i=m}^ni^k mod P$

$P,n,m<=10^{12},k<=2000$

差分表是多项式求和利器
对于多项式$f(n)=\Sigma_{i=0}^kc_in^i$
可以在$O(k^2)时间内求出\Sigma_{i=0}^Nf(i)$

首先求出差分表第0条对角线$d_0,d_1,d_2,...d_k$
有$f(n)=\Sigma_{p=0}^k(^n_p)d_p$
$\Sigma_{k=0}^n(^k_p)=(^{n+1}_{p+1})$
$\Sigma_{i=0}^Nf(i)=\Sigma_{i=0}^N\Sigma_{p=0}^k(^i_p)d_p=\Sigma_{i=0}^N(^i_p)\Sigma_{p=0}^kd_p=\Sigma_{p=0}^kd_p\Sigma_{i=0}^N(^i_p)=\Sigma_{p=0}^kd_p\Sigma_{i=0}^N(^i_p)=\Sigma_{p=0}^kd_p(^{N+1}_{p+1})$

由于P较大，会爆longlong，有必要使用Head算法。

对于组合数的计算，当然不能用逆元。
由于$\frac{(^n_m)}{(^n_{m+1})}=\frac{m+1}{n-m},(^n_0)=1$
用数组fac[m]记录组合数的因子，一开始fac[m]=n-m , 扫一边fac，用m+1约去fac的公约数。$\Pi fac_m=(^n_m)$

D1T3

Pool
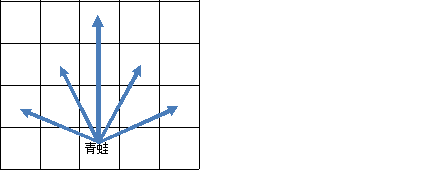
从前有两个青蛙王国，两个王国商业都非常繁荣。但是一块池塘阻碍了两国的商业往来。一次，两只青蛙在池塘的两岸，他们都希望到对岸去。我们可以将池塘看做一个n×m的矩形，在每个格子里，可能会有荷叶。青蛙必须踩在荷叶上，不能跳进水里。如图青蛙可以向他前方的5个有荷叶的地方跳去。

由于有的地方荷叶比较小，当一个青蛙从该荷叶上跳走之后，荷叶会沉入水底，两个青蛙也不能同时跳上这种荷叶。两个青蛙想知道有多少种方式使他们都到达对岸。第一个青蛙可以从第一行任何一个有荷叶的格子出发。第二个青蛙可以从最后一行任何一个有荷叶的格子出发。当第一个青蛙到达最后一行任何一个有荷叶的格子时，他就算到达了对岸。当第二个青蛙到达第一行任何一个有荷叶的格子时，他也算到达了对岸。请你帮助青蛙们计算有多少种方案可以让他们都到达对岸。
注：第一个青蛙只能向下跳，第二个青蛙只能向上跳。青蛙并不能跳出矩形区域。

Input

输入的第一行包含两个整数n，m。
第2至n+1行包含m个整数。若该数为0，表示该格子上没有荷叶，青蛙不能通过。若该数为1，表示该格子上的荷叶只允许一个青蛙通过。若该数为2，表示该格子上的荷叶可以允许两个青蛙都通过。

Output

输出的第一行包含一个整数，表示两个青蛙都到达对岸的方案数。由于结果可能非常大，输出答案模1000000007的结果。

这题状态显然：f[x1][y1][x2][y2]
判一下状态合不合法，直接转移。
值得注意的是要然x小的青蛙先走。枚举时|x1-x2|<=3

#include<cstdio>
#include<cstring>
#include<algorithm>

using namespace std ;

#define N 52
#define mo 1000000007 

int i , j , k , m , n , g[N][N] , v[N][N][N][N] , d[5][2] = { 1 , 2 , 1 , -2 , 2 , 1 , 2 , -1 , 3 , 0 } ;


typedef long long ll ;

ll  f[N][N][N][N] , dlt[N][N][N][N] ;


int l , r  ;


int main() {

    scanf("%d%d",&n,&m ) ;
    for( i=1 ; i<=n ; i++ ) 
        for( j=1 ; j<=m ; j++ ) 
            scanf("%d",&g[i][j] ) ;
    for( i=1 ; i<=m ; i++ ) if( g[1][i]!=0 ) 
        for( j=1 ; j<=m ; j++ ) if( ( i==j ) && ( g[1][i]==2 ) || ( i!=j )  &&  ( g[1][j]>=1 && g[1][i]>=1 ) ) {
            f[1][i][1][j] = 1 ;
        }
    for( int x = 1 ; x<=n ; x++ ) {
        for( int y = 1 ; y<=m ; y++ ) {
            if( g[x][y]==0 )  continue ;
            for( int a = max( 0 , x-3 ) ; a<=x+3 ; a++ ) {
                if( a > n ) break ;
                for(  int b = 1 ; b<=m ; b++ ) {
                    if( g[a][b]==0 ) continue ;
                    if( a==x && b==y && g[a][b]==1 ) continue ;
                    if( f[x][y][a][b]==0 ) continue ;
                    for( k=0 ; k<5 ; k++ ) {
                        int nx , ny ;
                        if( x<a ) {
                            nx = x + d[k][0] , ny = y + d[k][1] ;
                            if( nx < 1 ||  ny < 1 || nx > n || ny > m ) continue ;
                            if( g[nx][ny]==0 ) continue ;
                            if( nx== a && ny== b && g[nx][ny]==1 ) continue ;
                            if( nx-3>a || nx+3<a ) continue ;
                            ll *C = &f[nx][ny][ a ][ b ] , *B = &f[x][y][a][b] ; 
                            *C += *B  ;
                            *C %= mo ;
                        } else {
                            nx = a + d[k][0] , ny = b + d[k][1] ;
                            if( nx>n || ny<1 || nx < 1 || ny > m  ) continue ;
                            if( g[nx][ny]==0 ) continue ;
                            if( nx==x && ny==y && g[nx][ny]==1 ) continue ;
                            if( nx-3>x || nx+3<x ) continue ;
                            f[ x ][ y][nx][ny] += f[ x ][ y ][ a ][ b ] ;
                            f[ x ][y][nx][ny] %= mo ;
                        }
                    }
                }
            }
        }
    }
    ll ans = 0 ;
    for( i=1 ; i<=m ; i++ ) 
        for( j=1 ; j<=m ; j++ ) ans = ( ans + f[n][i][n][j] ) % mo ;
    printf("%lld",ans ) ;
}