[堆排序之一]图文说明，快速理解

前言：

在学堆排序的时候，第一份资料看的是算法导论，嚼着好晦涩，昏昏欲睡，不直观不好理解。于是又查阅了其他资料，果然网上各种总结更给力啊。

我根据自己的情况，把堆排序学习分成3部分：快速理解、深入理解原理和C++实现。自我感觉，这种安排对快速理解堆排序还是很有帮助的。

所谓“原创”，是在整理网友资料基础上，加上了一些自己的理解和感悟。

 

堆的定义：

堆（heap）是一种数据结构。定义：

n个元素的序列{k₁，k₂，…, k_n}当且仅当满足下列关系之一时，称之为堆。

     情形1：k_i <= k_2i 且k_i <= k_2i+1 

　 情形2：k_i >= k2_i 且k_i >= k_2i+1 

 其中i=1,2,…,n/2向下取整.

 

二叉堆的定义：

二叉堆是一种特殊的堆，它是完全二叉树或者是近似完全二叉树。

二叉堆满足二个特性：

1．父结点的键值总是大于或等于（小于或等于）任何一个子节点的键值。

2．每个结点的左子树和右子树都是一个二叉堆（都是最大堆或最小堆）。

当父结点的键值总是大于或等于任何一个子节点的键值时为最大堆（大根堆）。当父结点的键值总是小于或等于任何一个子节点的键值时为最小堆（小根堆）。

 

二叉堆的存储

二叉堆一般用数组表示。

(1) 若根结点存在序号0处， i 结点的父结点下标就为(i-1)/2。i结点的左右子结点下标分别为2i+1和2i+2。

(2) 如果根结点是从1开始，i 结点的父节点下标为 i/2，左右孩子结点分别是2i和2i+1。

堆排序：

对于堆排序，最重要的两个操作：

（1）构造初始堆；

（2）调整堆。

 

操作过程如下：

1)初始化堆：将R[1..n]构造为堆；

2)将当前无序区的堆顶元素R[1]同该区间的最后一个记录交换，然后将新的无序区调整为新的堆。

 

实例如下：

 给定一个整形数组a[]={16,7,3,20,17,8}，对其进行堆排序。

 首先根据该数组元素构建一个完全二叉树，得到

 

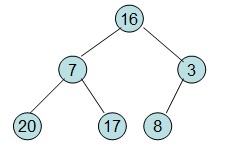
然后需要构造初始堆，则从最后一个非叶节点开始调整，调整过程如下：

20和16交换后不满足堆的性质，因此需重新调整

这样就得到了初始堆。

每次调整都是从父节点、左孩子节点、右孩子节点三者中选择最大者跟父节点进行交换(交换之后可能造成被交换的孩子节点不满足堆的性质，因此每次交换之后要重新对被交换的孩子节点进行调整)。

有了初始堆之后就可以进行排序了。

 

交换3和20，得到

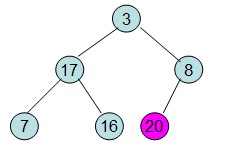
此时3位于堆顶不满堆的性质，则需继续调整

这样堆排序就完成了。

到这里，差不多应该理解堆排序的操作了，下面总结下堆排序的基本思想：

    1)将初始待排序关键字序列(R1,R2....Rn)构建成大顶堆，此堆为初始的无序区；

    2)将堆顶元素R[1]与最后一个元素R[n]交换，此时得到新的无序区(R1,R2,......Rn-1)和新的有序区(Rn),且满足R[1,2...n-1]<=R[n]; 

    3)由于交换后新的堆顶R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,......Rn-1)调整为新堆，然后再次将R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2....Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1，则整个排序过程完成。

下一篇：[堆排序之二]深入理解原理

参考资料：

[1] 维基百科：堆、二叉堆

[2] http://www.cnblogs.com/mengdd/archive/2012/11/30/2796845.html

[3] http://www.cnblogs.com/dolphin0520/archive/2011/10/06/2199741.html