【算法导论】动态规划之“钢管切割”问题

        动态规划，其实跟分治法有些相似，基本思想都是将复杂的问题分成数个简单的子问题，然后再去解决。它们的区别在于，分治法关注的子问题不相互“重叠”，而动态规划关注的子问题，多是相互“重叠”的。比如在快速排序中，我们将数据分成两部分，这两部分再分别快速排序的递归思想，也就是将整个问题的排序划分为子问题子数组的排序，但是这两个子数组的排序之间并没有相互联系，a子数组的排序不会因为b子数组的排序而得到任何“好处”或者“坏处”。但是有些时候，划分的子问题之间却是有联系的，比如下面的“钢管切割”问题：

        钢管切割原始问题：

        某公司生产长钢管，然后一般，会将钢条切断，变成不同长度，然后去售卖。其中有个问题是，不同长度的钢管的售价是不一样的，但是它们并不是完全按照比例来，比如2米的钢管售价要比3米的钢管售价要少，但是并不是2比3的比例。钢管的长度售价表如下：

长度i	1      2      3      4      5      6      7      8      9      10
价格Pi	1      5      8      9     10    17    17     20    24    30

        于是问题就来了，比如30米长的钢管，要如何切割，切割成多长的几条，才能让售价最高，收益最高呢？

        求解最佳收益和对应的分配方法：

        朴素算法：

        最简单直接的想法，就是用暴力破解，n长的钢管，可以分解成i长和n-i长的两段，因为i可以从0~n取值，所以我们可以对i不进行继续切割，于是对于长为i的这一段，可以直接调用价钱数组p[i]来得到价钱，然后加上对n-i递归调用求最优收益的函数的返回值。在过程之中记录这些组合的最优收益，等循环结束的时候，就能得到最优的收益价钱。

        假设r[n]代表的是n长的钢管的切割最佳收益值，数组p代表上面表中的价格，其中p[0]=0，从p[1]~p[10]对应上面表中的数据，那么按照上面的想法，有公式：

        r[n]=max(p[i]+r[n-i])，i从1到n，当n=0时，r[n]=0，因为0长的钢管售价当然为0。

        于是给以下实现代码：

int cut_rod(int* p, int n) {
	if (n == 0) {
		return 0;
	}
	int q = -1;
	for (int i = 1; i <= n; i++) {
		/*
		 * 将n长的钢条，分成i和n-i的两段，i长的那段不切割，而n-i的那段求最大
		 * 切割收益方式，然后相加；而q值是所有的组合中，最大收益的那个
		 */
		q = max(q, p[i] + cut_rod(p, n - i));
	}
	return q;
}

        这种方法比较容易理解，但是性能是不是好呢？

        可以简单的以n=4的情况来看一下：

        n=4的划分(其中前面的那一段是直接使用p[i]，后面一段调用函数来求最佳收益)：

        cut_rod(p,4)的划分可能：

        ①1长和3长：p[1]+cut_rod(p,3)

        ②2长和2长：p[2]+cut_rod(p,2)

        ③3长和1长：p[3]+cut_rod(p,1)

        ④4长和0长：p[4]+cut_rod(p,0)

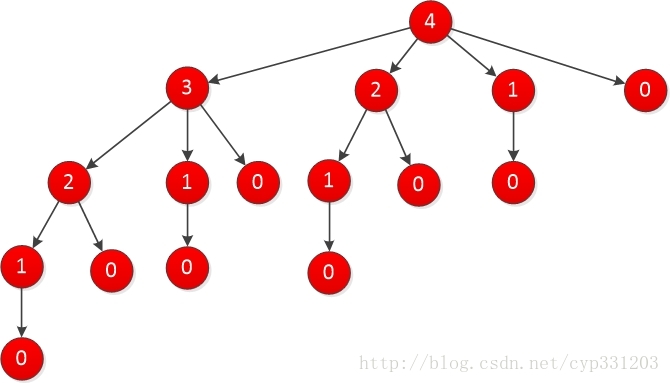
        而其中cut_rod(p,3)又可以划分为数组p中元素与cut_rod(p,0)，cut_rod(p,1)和cut_rod(p,2)；以此类推，可以给出一种以递归调用树的形式展示cut_rod递归调用了多少次：

        

        不难从图中看出，做了大量重复工作，以n=2的节点为例，分别在n=4和n=3的时候都被调用了。根据上图，可以给出递归调用次数的一个公式，假设T(n)表示cut_rod第二个参数为n时的调用次数，T(0)这时候是为1的，因为根结点的第一次调用也要算进去。于是有：

                                                                                T(n)=1+T(0)+T(1)+...+T(n-1)

        使用归纳法，可以比较容易的得出：T(n)=2^n。

        指数次幂的调用次数，显然太大，我们稍微让n大一点，则会让整个过程变的漫长。

        动态规划算法：

        而实际上我们不需要在每次都去重新计算cut_rod的在n=2时的结果，只需要在第一次计算的时候将结果保存起来，然后再需要的时候直接使用即可。这其实就是所谓的动态规划算法。

        这里的思路有两种，一种叫带备忘的自顶向下方法，是顺着之前的代码，当需要的时候去检查是不是已经计算好了，如果是，则直接使用，如果不是，则计算，并保存结果。第二种思路是自底向上方法，不论需不需要，先将子问题一一解决，然后再来解决更一级的问题，但要注意的是，我们需要先从最小的子问题开始，依次增加规模，这样每一次解决问题的时候，它的子问题都已经计算好了，直接使用即可。

        带备忘的自顶向下方法:

int memoized_cut_rod_aux(int* p, int n, int* r) {
	if (r[n] >= 0) {
		return r[n];
	}
	int q = -1;
	if (n == 0) {
		q = 0;
	} else {
		for (int i = 1; i <= n; i++) {
			q = max(q, p[i] + memoized_cut_rod_aux(p, n - i, r));
		}
	}
	r[n] = q;
	return q;
}

/*
 * 自顶向上的cut-rod的过程
 */
int memoized_cut_rod(int* p, int n) {
	int* r = new int[n + 1];

	//初始化r数组，r数组用来存放，某种解决方案的最大收益值，对于n长的钢条而言，有n+1种切割方案，所以数组n+1长
	for (int i = 0; i <= n; i++) {
		r[i] = -1;
	}
	return memoized_cut_rod_aux(p, n, r);
}

        自底向上的方法：

/*
 * 自底向上的方式，先计算更小的子问题，然后再算较大的子问题，由于较大的子问题依赖于更小的子问题的答案，所以在计算较
 * 大的子问题的时候，就无需再去计算更小的子问题，因为那答案已经计算好，且存储起来了
 */

int bottom_up_cut_rod(int p[], int n) {

	int* r = new int[n + 1];

	r[0] = 0; //将r[0]初始化为0，是因为0长的钢条没有收益
	for (int j = 1; j <= n; j++) {
		int q = -1;

		/*
		 * 这里不用i=0开始，因为i=0开始不合适，因为这里总长就是为j，而划分是i和j-i的划分，如果i等于0，那么
		 * 就意味着要知道r[j-0]=r[j]的值也就是j长的最好划分的收益，但是我们这里不知道。而且对于p[0]而言本身就没有意义
		 * p数组中有意义的数据下标是从1到n的
		 */
		for (int i = 1; i <= j; i++) {
			q = max(q, p[i] + r[j - i]); //
		}
		r[j] = q;
	}
	return r[n];
}

上面两种算法的时间复杂度都是O(n^2)。

        重构解

        上面的代码只给出了最优的收益值，但是却没有给出最优收益到底是在那种切割分配方式下得到的，比如说n=9时，最佳收益为25，要分成3和6两段。这里可以使用另一个数组s来存储分段情况，比如s[9]存储3，然后我们让n=9-3，就可以得到s[6]的最佳分段情况，发现就是6，于是就不需要继续。

只需要将代码稍微修改即可达到目的：

#include<iostream>

using namespace std;

/*
 * 存储结果的结构体，里面包含r和s两个数组，分别保存最佳收益和最佳收益时的分段数值
 */
struct result {
	int* r;
	int* s;
	int len;
	result(int l) :
			r(), s(), len(l) {
		r = new int[len];
		s = new int[len];
		r[0] = 0;
	}

	~result() {
		delete[] r;
		delete[] s;
	}
};

result* extended_bottom_up_cut_rod(int p[], int n) {
	result* res = new result(n + 1);
	int q = -1;

	//外层的循环代表的是保留的不切割的那段
	for (int i = 1; i <= n; i++) {

		//内层的循环代表的是要分割的，且要求出最佳分割的那段
		for (int j = 1; j <= i; j++) {
			if (q < p[j] + res->r[i - j]) {
				q = p[j] + res->r[i - j];
				res->s[i] = j;
			}
		}
		res->r[i] = q;
	}
	return res;
}

int main() {
	int p[] = { 0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30 };

	int n = 9;

	result* res = extended_bottom_up_cut_rod(p, n);

	cout << "最佳收益：" << res->r[9] << endl;

	//循环输出实际的最佳分割段长
	cout << "分段情况：";
	while (n > 0) {
		cout << res->s[n] << ' ';
		n = n - res->s[n];
	}

	delete res;

	return 0;
}

运行上面程序，我们就可以的得到长度为9的钢管的最佳收益以及对应的切割情况：

最佳收益：25
分段情况：3 6