不同子序列

LeetCode-Problem115-典型的二维动态规划问题，且可转一维

1）题目

2）分析

• 初步思路：两个子序列问题，通常都是二维及其以上的dp可解；
• 状态分析1：考虑二维dp，定义$state$形式为$dp[i][j]$，那么$dp[i][j]$的意义呢？dp[i][j]的极端的值（或者说端点）是$dp[0][0]$或者$dp[n][m]$，其中$n、m$分别为$s、t$长度；两个极端值有一个是我们要求的目标，具体是哪一个呢？
• 状态分析2：这里哪个都可以，如果选取$dp[0][0]$，则我们定义$dp[i][j]$表示$s[i:n]（左闭右开，下同）、t[j:m]$的子序列关系，此时dp[0][0]表示s[0:n]含有多少个t[0:m]这样的子序列；选取$dp[n][m]$时，$dp[i][j]$表示$s[0:i]$含有多少个$t[0:j]$子序列；两者只是方向不同，这里选择dp[0][0]作为目标；
• 状态方程1：有了$state$的形式和意义，接下来就是写出状态转移的方程；通常都是比较dp[i][j]和周边区间如dp[i+1][j]、dp[i][j+1]或者dp[i+1][j+1]的关系；这里针对子序列问题，考虑$s[i]、t[j]是否相同$，可以写出如下状态方程：
  $$dp[i][j]=\{\begin{array}{ll}dp[i+1][j+1]+dp[i+1][j]& \text{if }s[i]==t[j]\\ dp[i+1][j]& \text{if }s[i]\ne t[j]\end{array}$$
• 状态方程2：上述方程表示，如果$s[i]==t[j]$，如$s="bbag"$ 和 $t="bag"$，$s[0]=t[0]=‘b’$，此时$s[0]$可以用来匹配$t[0]$，也可以放弃匹配，由$s[1:]$等后续序列进行匹配；而如果$s[i]\ne t[j]$，则可能的匹配子序列存在于$s[i+1:]和t[j]$之间；
• 初始状态：上述状态方程的初始状态是$dp[n][-]和d[-][m]$；$i=n$表示s=""，此时$dp[n][-]=0$；$j=m$表示t=""，此时$dp[-][m]=1$；注意dp[n][m]=1，代表s="“和t=”"也能匹配一次；
• 举例：以s="babgbag"和t="bag"为例，状态方程初始化如下图@windliang
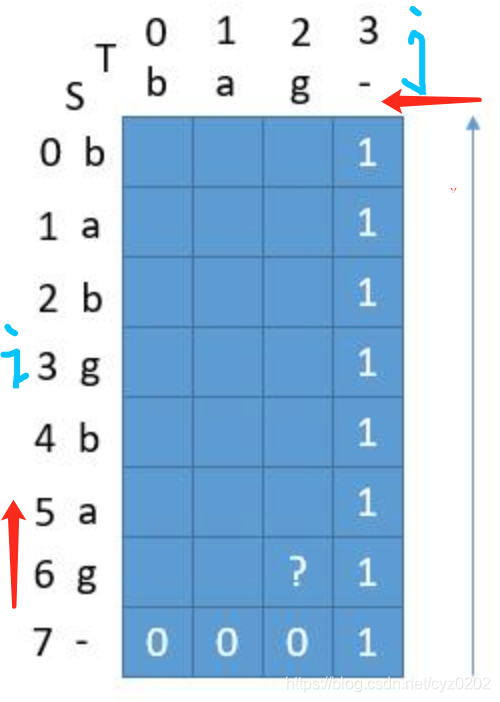
• 代码：

class Solution:
    def numDistinct(self, s: str, t: str) -> int:
        # 二维(or一维)，并以t为dp数组
        # 动态方程如下
        # dp[i][j] = dp[i+1][j+1] + dp[i+1][j] or   # if s[i]==t[j]
        #            dp[i+1][j]                     # else

        dp = [[0 for _ in range(len(t)+1)] for _ in range(len(s)+1)]
        for i in range(len(s), -1, -1):  # 初始化dp[-][n]=1，注意dp[m][-]=0已经默认初始化了
            dp[i][len(t)] = 1
        for i in range(len(s)-1, -1, -1):
            for j in range(len(t)-1, -1, -1):
                if s[i] == t[j]:
                    dp[i][j] = dp[i+1][j+1] + dp[i+1][j]
                else:
                    dp[i][j] = dp[i+1][j]
        return dp[0][0]

• 二维->一维：从动态方程可以看出，$dp[i][j]$只跟临近一个step的状态有关系，如$dp[i+1][j+1]$，这就为二维dp转变为一维dp提供条件，因为一维dp数组本身可以分更新前和更新后的值，天然的就可以区分一个step的变化；代码如下：

class Solution:
    def numDistinct(self, s: str, t: str) -> int:
        # 二维->一维，并以t长度为dp数组长度
        # 动态方程如下
        # dp[i][j] = dp[i+1][j+1] + dp[i+1][j] or   # if s[i]==t[j]
        #            dp[i+1][j]                     # else
        dp = [0 for _ in range(len(t)+1)]
        dp[-1] = 1  # 边界条件，表示t=""，则s有1个相应子序列
        for i in range(len(s)-1, -1, -1):  # s逆向
            for j in range(len(t)):  # t正向，以符合更新要求
                if s[i] == t[j]:  # 注意这里只需判断s[i]==t[j]的情况，不等的情况根据上述方程和dp的定义，dp[j]会保持不变，所以不需要更新，读者可仔细看一下这个巧合；
                    dp[j] += dp[j+1]
        return dp[0]

• 总结：熟悉两个序列关系计算的二维动态规划使用，本题属于区间型动态规划