从韩信点兵和勾股弦说起—— 漫谈基础数学的古今中外

从韩信点兵和勾股弦说起—— 漫谈基础数学的古今中外

前言

　　基础数学的范畴，大体上也就是现代中学和大一数学课程中所要学的代数、几何与分析的基础知识；它不但是数学的根本，也是整个科技发展的基础，可以说是人类理性文明中的重大篇章。由此可见，我们今天所要谈论的题目，即使是漫谈也只能择其精要，长话短说，也许可以提纲挈领地略述其梗概，整理出其中几条主线来。现在且让我们就以中国古算中两个辉煌成就：韩信点兵与勾股弦分别作为代数与几何逐步演进的线头，来分析一下其中发展的脉络。

Ⅰ.韩信点兵

　　相传的韩信点兵法又叫做孙子算法，例如：在广场中有士兵约一千左右，若令其分别以7人，11人，13人一组自行组合，设其余额分别为1人，5人，8人。试求其确切人数。
　　韩信点兵的基本想法是分组结合，亦即把上述由给定余数反求原数的问题赋予下述三个简化的特例来求解，即余数之中只有一个为1，其他皆为0的简单而又基本的情形。以上述点兵问题为例，则是先求解下列之$x_1，x_2，x_3$；而所求之$x$和$x_1+5x_2+8x_3$只差一个1001的倍数，即$x_1，x_2，x_3和x$分别以7，11，13除之前的余数如下表所列：

表Ⅰ-1

因为$x_1$ 被11，13整除，所以它是143的倍数，即$x_1=143y_1$，再者$143y_1$ 和$3y_1$ 被7整除的余数截然相同，由此易见$y_1=5$ ;$x_2,x_3$ 的求法同此。
$\Rightarrow$ $$\left\{ \begin{array}{} x_1=143y_1\\ x_2=91y_2\\ x_3=77y_3 \end{array} \right.$$
$\Rightarrow$ $$\left\{ \begin{array}{} y_1=5\\ y_2=4\\ y_3=12 \end{array} \right.$$
$\Rightarrow$ $$x\equiv x_1+5x_2+8x_3(1001)$$
由上述$x_1，x_2，x_3$ 之解即可看出$x=918$ 。上述算法当然可以直接推广到分别对于k个互素的除数的给定余数反求原数，这种剩余问题，即


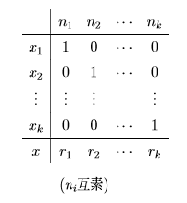
表Ⅰ-2

　 $\Rightarrow$ $$\left\{ \begin{array}{} x_1=n_2 \cdots n_k y_1\\ x_2=n_1n_3 \cdots n_k y_2\\ \cdots\\ x_k=n_1 \cdots n_k-1 y_k \end{array} \right.$$
　 $\Rightarrow$ $$x \equiv \sum r_ix_i(n_1 \cdots n_k)$$
这也就是在数论中的中国剩余定理（Chinese Remainder Thearem）。其实，它不仅仅是数论中的一个重要定理，数学中有好多重要的公式与解法，其根本都是韩信点兵的直接推算，例如：
　　多项式的插值公式：一个多项式$f(x)$ 被$(x-a)$ 除的余式就是$f(a)$ ，多项式函数的一个基本性质是一个n级多项式$f(x)$ 被它在$n+1$ 个点的值所唯一决定。多项式的 插值问题也就是要由一个n次多项式$f(x)$ 在给定的$n+1$ 个点$\{a_i;0 \leq i \leq n \}$ 的函数值，亦即从$\{b_i=f(a_i);0 \leq i \leq n \}$ 去反求上述两组$\{a_i\}和\{b_i\}$ 所唯一确定的多项式。将上述插值问题和韩信点兵的剩余问题两相比较，不难看出，只要把数改成式，除数改成除式$(x-a_i)$ ,则余式就是$f(a_i)=b_i$ 。所以前者就是后者在多项式除法上的直接推广。同样地，把韩信点兵的基本想法用到插值问题上，即有：


表Ⅰ-3

则有：$f(x)=\sum_{i=0}^n b_if_i(x)$ 。
再者，由余式定理的推论可得$f_0(x)$ 必然是$\prod_{j=1}^n (x-a_j)$ 的倍式[因为$f(a_j)=0;1\leq j\leq n$] ,由此易见
$$f_0(x)=\prod _{j=1}^n (x-a_j)/ \prod_{j=1}^n (a_0-a_j)$$
[这样使得$f_0(a_0)=1$ ]。
同理可得 $$f_i(x)= \prod_{j \neq1}(x-a_j)/ \prod_{j \neq 1}(a_i-a_j)$$
所以韩信点兵在多项式的框架中的直接推广也就是代数中的Lagrange插值公式。
　　在我们进一步探讨“韩信点兵”的其他推广及其深化影响之前，且让我们先来分析一下，他这种分解组合的想法的数理内涵何在？归根究底，整数的乘法乃是由加法的浓缩而得的；例如$5·a$ 其实就是5个a相加的总和，由此可见，下述分配律
$$n·a+m·a=(m+n)·a$$
其实也就是简明扼要的总结了加与乘之间的起承关系的特征性质！而分配律就是韩信点兵的数理依据。在数学发展史上，韩信点兵开创了如何运用分配律来达成分解组合，从而简明扼要地解决各种各样的线性问题（linear problems）的先河与典范！因为这种分解组合的方法的用途是如此广泛，而用它来解决线性问题又特别简洁有力，把它加以抽象化，系统化，所发展成的一门基础数学目下所称之为线性代数（Linear Algelra）者，究其本质，线性代数就是分配律的代数，而韩信点兵则是线性代数的基本方法的起始源头，例如线性方程组，线性微分方程等等，都是这种分解组合的基本想法的直接推广，洋洋洒洒，多彩多姿，不胜枚举。
　　今天限于时间，暂且打住，让我们改弦更张，中国古算中的几何。

Ⅱ.勾股弦与出入相补

　　我们在史籍上读到大禹治水，以及春秋、战国、秦、汉的种种大型水利工程，如今变迁，硕果仅存者首推都江堰，它两千多年来依然故我，一直在造福着成都平原上的世世代代，任何人到了都江堰都情不自禁地惊叹中国古代工程师卓越的智慧的与匠心，令人神往。我们接着要谈一谈的中国古算中的测量原理，也就是他们在实践中体会结合而得者。也许当年很可能是以一套测量技术的形式世代流传于工匠之间，其实他们已经是一套简明扼要的“定量平面几何的基础理论”。
　　话说当年，他们以长方形面积等于长乘宽这个基本公式为起点，利用简单的割补，推算而得平行四边形和三角形的面积公式，然后再利用分割和出入相补去推算出下述两个平面测量上的基本公式，即
（1）勾股弦公式：勾方加股方等于弦方（$a^2+b^2=c^2$)

[由实线和虚线所示的两种分割计算$（a+b$）的平方]
（2）出入相补：如图二所示，在一个任给的矩形的对角线上任取一点$P$，它把过该点的水平线和垂直线分别分为$l,l'和h,h'$；再者有由面积的出入相补，即可看出图二之中的两个斜线所示的矩形面积相等，即得下述基本比例式：


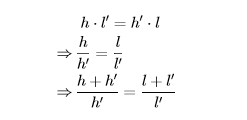
勾股弦这个直角三角形三边之间的基本公式，在西方起源与巴比伦，在Euclid Elements中给有两个证明，但都不如上述中国古证来的简洁，再者，在“出入相补”的应用时，通常是将由等面积直接得出的比例式两旁加1而得到的$（h+h'）/h'=(l+l')/l'$;由图二可见，这其实就是两个相似的直角三角形的对应直角边之间的比例式，由此可见中国古算中的“出入相补”其实就是“相似三角形定理”在直角三角形的特例。骤看起来，前者似乎只是后者的一个特例，其实，任何一对相似三角形都可以用垂直线分割成两对相似的直角三角形的组合，所以用出入相补加上勾股弦去推导一般的相似三角形定理，只是这么简简单单的一步，这也就是在中国古算用勾股弦和出入相补去解答各种各样的测量问题皆能无往不利的道理。
　　将中西古文明定量平面几何两相比对，在本质上都自然而然的发现了勾股弦和相似比例式这两个基本定理，可以说是大同小异，但是在处理方式上确实各有所长，是数学史上一次耐人寻味的殊途同归，为了把这一点解说明白，让我们接着谈一谈古希腊定量几何基础理论的进化历程。

Ⅲ.古希腊的几何基础论

　　话说当年，古希腊文明继承了巴比伦和埃及文化，在东地中海沿岸的诸多城邦蓬勃发展，在其上层阶级中，不乏好学有识之士，提创学术; 而对于几何学、 天文学的研究, 尤为热衷, 蔚为风尚。 在整个人类文明发展史上, 是一个难得的黄金时代, 在这里我们只是择其精要, 概述其重大者之一二：
　　(1)定性平面几何： 以全等形 (亦即叠合) 和平行为主题;“三角形的 S.A.S 全等条件”和“三角形内角和恒为一平角”为起点,推导了大量关于全等形和平行性质上的定理。若对它们的论证作一系统分析, 则不难看到其论证的基本工具其实只有两个, 那就是:
(i) 等腰三角形的诸多特征性质的转换使用。
(ii) 平行四边形的诸多特征性质的转换使用。

图三

　　 长话短说, 前者是运用平面的对称性的“不二法门”而后者则是利用平行性质的“不二法门”, 而认清上述两者业已构成定性平几的纲要, 则是精简“定性平几” 的课程与教学的自然途径
　　(2) 由定性平几迈向定量平几 (由全等到相似):在定性的研讨中, 对于两个同类的几何量之间, 只讨论其大, 小或相等关系。例如两个线段, 只问其长短或是否等长? 但是到了定量几何,我们就要对于两个线段确定其长度上的比值来度量其差别。例如$a : b = {m \over n}$或$a ={m \over n}b$与 na = mb 同义。再者, 因为长度是各种各样几何量之中的最最基本者, 所以长度的度量也就自然是定量几何的起步,在这里可以看到中、西的古代几何学者在观点上的分歧。前者采取实用的观点而后者则采取理论的观点。在实用上,一个给定线段的度量可以用刻有足够小的分单位的“直尺”逐段丈量, 而很小的余段则可略去不计, 因为它业已小于度量过程或实用上需求的准确度了!但是在古希腊的理论探讨中,他们就认识到下述长度度量上的基本问题:
　　可公度性 (Commensurability) 和长度度量基本问题：若存在有一个公尺度 $c$使得两个给定线段$a,b$ 恰好都是它的整数倍, 即$a = mc,b = nc$ 则称$a,b$为可公度者,这样的两个线段在长度上的比值当然就可以定义为分数${m \over n}$。是否任何两个线段总是可公度的呢?
　　上述“可公度性是否普遍成立”这个问题的基本重要性可以先从正反两面来探讨其内涵, 若上述问题的答案是肯定的, 则任何两个线段的长度之比恒为一分数。反之, 若存在有不可公度的一对对线段, 则它们的长度之比不但不是分数, 而且其确切意义尚有待定义!古希腊几何学在这一点上颇费周章, 是经历了一番挫折与奋斗才成功的, 直到今日再来回顾这一段史话, 依然是发人深思的。
　　大约在公元前五、 六世纪, 他们先是主观地把“可公度性的普遍成立” 看成是不证自明的一个“公理”(Axiom), 从而用全等形定理和平行分割, 对于定量几何中的基本定理如矩形面积公式, 毕氏定理 (亦即勾股弦) 和相似三角形定理等逐一给以严格论证, 建立了一个“定量平几的基本理论”。 其中毕氏学派在这方面贡献良多。
　　例如下述平行分割就是对於矩形面积公式和相似三角形定理的证明要点:
(i) 矩形面积公式之证明:
　　设 $u$是取定的单位长, 基于“可公度性普遍成立”这个 “公理”, 矩形的长和宽分别都是 $u$ 的分数倍, 亦即$l= {m \over n}u,w={p \over q}u$则 $\square (l,w) 和 \square (u,u)$可以分别平行分割成$m · p$ 和$n · q$ 个以${1 \over n}u$和${1 \over n}u$为边长的小矩形, 这也就证明了
$$\square (l,w): \square (u,u)={mp \over nq}=(l:u)×(w:u)$$
(ii) 相似三角形定理的证明:
　　设$△ABC$ 和 $△A'B'C'$的三个内角对应相等, 再者由“可公度公理”$\overline{AB}:\overline{A'B'}$是一个分数${m \over n}$,则用下图所示的平行分割, 可以把它们分割成 ${m ^2}$和${n^2}$ 个全等的小三角形, 这样就可以证明
$$\overline{ AB}:\overline{A ′ B ′} =\overline{ AC}:\overline{A ′ C ′}=\overline{ BC}:\overline{B′ C ′} ={m \over n}$$
　　　　　　　　　　　
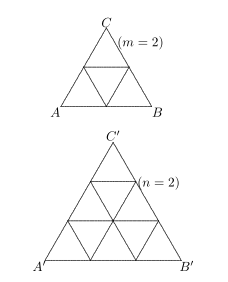
图四
　　 　　　　　　　　　　　　　　　　
　　(3) 不可公度量的发现: 大约在毕氏本人去世后不久, 其门人 Hippasus 一直在鍥而不捨地钻研 “可公度是否普遍成立? ”这个基本问题。由可公度性的定义, 不难看到两个可公度的线段$a,b$之间, 存在著一个最长的公尺度 $c$, 而且可以用“辗转丈量法”由$a,b$求得$c$ 。即先以较短者 $b$逐段丈量$a$, 若恰能整量,则$b$本身就是所求的最长公尺度, 不然即得一比 $b$短的余段 $r _1$; 再以 $r _1$ 逐段丈量$b$, 若恰能整量, 则 $r _1$即为所求者, 不然则又得一余段 $r _2<r _1$ ; 我们又可以用$r _2$逐段丈量$r _1$ 如此辗转丈量, 若 $r _k$ 恰能整量 $r _{k-1}$ , 则$r _k$就是所求者。 上述辗转丈量法求最长公尺度和大家所熟悉的辗转相除求一对整数的最大公因子是密切相关、 相通的, 在当年很可能后者起源于前者。
　　假如我们对上述求法稍加分析, 就会看到下列两点: (i) {$a,b$} 是可公度的充要条件就是上述丈量法在有限步即已终止, 反之, 若上述丈量法永无止休, 则 {$a,b$} 就是 不可公度者。(ii) 要注意, 可不可以公度或辗转丈量是否永无止休都是纯理论的问题, 因为在实用的度量上, 一来误差是不可避免的, 二来也无法进行无限微小的丈量! 所以我们所讨论的乃是纯理论境界中的一个问题, 其重要性则在于定量几何基础理论的建筑上。 总之,可不可公度? 辗转丈量是否永无止休? 是只有从纯理论的论证中去探讨的! 是无法由实践加以检验者也!
　　话说当年, 有一天 Hippasus 在沙盘上对於正五边形作一番数理分析时发现了一个令他震惊的事实, 那就是一个正五边形的对角线长和其边长是不可公度的!因为他的数理分析证明了对于这样一对线段的辗转丈量肯定是永无止休的! 他这个石破天惊的发现, 基于下述图解:


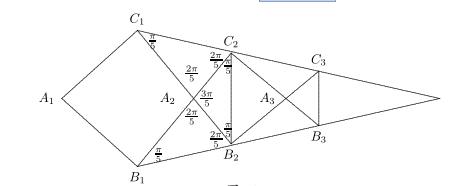
图五

如图五所示, $A _1 B_ 1 B_ 2 C_ 2 C_ 1$ 是一个正五边形, 只要用当时业已熟知的二点, 即 (i) 三角形内角和恒为一平角, (ii) 等腰三角形的两底角相等, 反之亦然, 对于上述图形加以分析, 即可得出其中所标记的那些角度, 和$\overline{C_ 1 A_ 2} = \overline{C _1 C_ 2} ,\overline{A _2 B _2 } = \overline{ A _2 C _2 }$。再者, 若取 $B_ 3 ,C _3$使得 $\overline{B_ 2 B_ 3} = \overline{C _2 C_ 3}=\overline{A _2 B _2 }$则不难验证$A_ 2 B_ 2 B_ 3 C_ 3 C_ 2$ 又是一个正五边形, 而且原来的边长成为其对角线长。 令{a,b} 分别是原给的正五边形的对角线长和边长, $r_ 1$是用 $b$丈量$a$ 所得的余段, 上图证明 {b,$r _1$ } 就是那个小一号的正五边形的对角线长和边长。 由此可见, 逐步辗转丈量下去, 每一次所做的总是用一个正五边形的边长丈量其对角线长, 所以当然是永无止休的!(只是那个正五边形愈来愈小吧了。) 这也就证明了当年认为不证自明, 用来作为定量几何的基本“公理”者, 其实是错误的! 不可公度的情形是存在的!
　　(4)逼近法和几何基础论的重建 :上述Hippasus 不可公度量的存在性的论证, 我们现在可以把它作为一个划时代的发现来欣赏, 它简洁清新, 引人入胜, 但是对於当年的古希腊几何学家们, 这简直是天摇地动的大地震 (Geoquake), 它把他们引以自豪的几何基础论震撼得摇摇欲坠, 因为所有基于“可公度性普遍成立” 这个“公理”的证明都显然是不完整的了! 其实, 它们只是对于可公度的这种特殊情形的证明。 Hippasus 这个惊人的发现, 当年的确使得古希腊的学界, 特别是毕氏学派非常难堪 , 据说当年毕氏学派曾试图在门人中强制保密; 而 Hippasus 这位学者则实在难以忍受这种抹杀真理的欺世行为,终于因洩漏真理而牺牲了生命呢!
　　如今来回顾这一段史话, 毕氏学派对于这样伟大的一个发现, 其反应竟是全然非理性的, 实在令人叹惜莫名。 一个实事求是的理性对待是: 面对不可公度性客观存在这个事实, 承认当时基於“可公度性普遍成立”所建立的几何基础论的不完备性, 然后, 再去致力寻求其补救的方法。 此事一直等到 Eudoxus首创逼近法 (approximation) 才得到突破性的成功, 下面就让我们对於 Eudoxus 这个伟大创见, 作一简要的介绍, 其实这也就是分析学的发祥地。
　　逼近法与几何基础论的重建:现在以相似三角形为例, 来说明 Eudoxus 当年创逼近法来完成其“补证”的基本想法, 当两个三内角对相等的三角形中有一对对应边的比值是一个分数${m \over n}$时, 前述的证明业已证明其余两对对应边的比值, 也等于${m \over n}$。所以有待补证的情形是对应边不可公度的情形。 Eudoxus指出, 在这种情形, 对应边的比值不但不是分数, 而且其确切意义尚有待明确。 再者, 两对不可公度的线段的两个“比值”之间的大小或相等关系也还有待加以明确定义, 他首先提出下述比较法则:即
$$a:b>{m \over n}⇐⇒na>mb$$ $$a:b<{m \over n}⇐⇒na<mb$$
再者, 他又提出下述长度的可比性: 对于任给两个线段$a,c,$ 恒有足够大的正整数$m$ 使得$mc > a$ [不管$a$有多长, $c$有多短]
　　设 a,b 是一对给定线段, 且为不可公度者; n 是一个任给正整数, 取 $c ={1 \over n}b$为尺度来丈量$a$。由上述原理，恒有一个唯一的$m$使得 $${m \over n}<a:b<{m+1 \over n}$$ 亦即$a:b$可以被夹逼在两个差额只有${1\over n}$的分数之间。 当$n$ 无限增大时,${1\over n}$显然可以小到任意地小。 用现代的术语来说, 就是 $a : b$可以用分数去无限逼近之! 这样也就充分地剖析了下述定义的合理性。
　　定义: 若对任给正整数 m,n 恒有
$$na\begin{Bmatrix} > \\ < \\ \end{Bmatrix}mb⇐⇒na^\prime\begin{Bmatrix} > \\ < \\ \end{Bmatrix}mb^\prime$$
　　(亦即两者恒为同步)
　　则定义为$a:b=a^\prime:b^\prime$。
若存在有一对 $m,n$ 使得 $na > mb$但是$na ′ < mb ′$; 则定义为$a : b > a ′ : b ′$; 反之, 若有 $na < mb$但有 $na ′ > mb ′$ 则定义$a : b < a ′ : b$。
　　接着, Eudoxus 就用逼近法简洁地补足了定量几何中原先只是对于可公度的情形具有证明的那些基本定理。 现在以相似三角形定理为例, 说明他用逼近法所作的补证:
　　设 $△ABC$和$△A'B'C'$ 的三内角对应相等,而$\overline{ AB}$ 和 $\overline{A ′ B ′}$ 是不可公度的, 我们要用上述定义来证明三对对应边的比值是相等的, 亦即下述不等关系的同步性是对于任给正整数, m, n 恒成立的: $$n\overline{ AB}\begin{Bmatrix} > \\ < \\ \end{Bmatrix}m\overline{A ′ B ′}$$ ⇐⇒ $$n\overline{ AC}\begin{Bmatrix} > \\ < \\ \end{Bmatrix}m\overline{A ′ C ′}$$ ⇐⇒ $$n\overline{ BC}\begin{Bmatrix} > \\ < \\ \end{Bmatrix}m\overline{B ′ C ′}$$
兹证之如下: 若$n\overline{ AB} > m\overline{ A ′ B ′}$ , 则可在线段$\overline{ AB}$ 上取 $B ^∗$点, 使得 $n\overline{ AB^ ∗} = m\overline{ A ′ B ′}$;过$B ^∗$ 的平行线交$\overline{ AC}$ 于$C^∗$ 点, 则有$△AB ^∗ C ^∗$ 和$△A ′ B ′ C ′$的三内角对应相等。
由先前业已得证的可公度的情形即得 $$\overline{ AC^ ∗}:\overline{ A ′ C ′}=\overline{ B^*C^ ∗}:\overline{ B ′ C ′}$$ $$=\overline{ AB^ ∗}:\overline{ A ′ C ′}={m \over n}$$ 所以 $$n\overline{ A C}>n\overline{ AC^ ∗}=m\overline{ A ′ C ′}$$ , $$n\overline{ B C}>n\overline{ B^*C^ ∗}=m\overline{ B ′ C ′}$$ 同理可证 $$n\overline{ A B}<m\overline{ A ′ B ′}⇒n\overline{ A C}<m\overline{ A ′ C ′}和$$ $$n\overline{ B C}<m\overline{ B ′ C ′}。$$
这也就是 Eudoxus 当年对于相似三角形在不可公度的情形的补证
　　不可公度性的存在对于古希腊几何基础论的严峻挑战, 历经半世纪, 如今不但可以用逼近法加以简洁的证明, 逼近法还给整个数学, 开拓了广阔的天地
　　古希腊的几何学经历这样一段转折, 奋斗与创造, 才真正脱胎换骨, 趋于成熟, 至于往后,Euclid 之成书,Archimede 对于 Eudoxus 逼近法的拓展,Appolonius 对于圆锥曲线的研究可以说是水到渠成的更上层楼。今天关于古希腊的几何史话也就此打住, 下面且让我们谈一些近代的数学进展。

Ⅳ.向量代数与解析几何

　　几何学所研究的课题就是我们和宇宙万物所在的空间的本质，宇宙间一切事物和现象都自然地蕴含着空间的性质，而且也永远就其制约！由此可见，几何学当然是一切自然科学的基础。再者，归根究底，由于我们所生存的大气层是一个高度透明，阳光普照的环境，所以良好的视觉是大有利于生存的一种本能。因此，漫长的进化历程中自然而然的赋予我们人类以极佳的视觉与空间直觉。可以说每一位正常人都与生俱来有相当好的几何天赋。由此可见，几何学成为人类文明中的“第一科学(Number one Science)”实非偶然，再者，空间的本质既简朴自然，又博大精深，所以几何学的基础理论在古希腊时代也已基本完备。但是空间本质的精微之处，例如平行性的真谛，困惑了几何学家近两千多年，一直到十九世纪非欧几何、微分几何的发展，才终于拨云见日，得见精微，但是此事说来话长，难以在此作一简短介绍。我们今天第四个也是最后一个题材，让我们谈一谈向量代数与解析几何。因为它更加基本实用，而且和前面三个呼应和连贯性也多得多。
　　十七世纪笛卡尔和费马开创解析几何学，乃是代数学与几何学这两大支流会和、会师之处，是整个数学发展史上的头号大事，其影响极为深远。而微积分的诞生则可以说是这一会师后的第一大产物，从纯几何的观点来看，解析几何是定量几何顺理成章的更上层楼的自然发展。因此让我们接着上一主题，先来分析一下解析几何和定量几何之间的起承关系。
　　古希腊和中国古算的定量几何中，都是以面积公式，勾股弦（亦即毕氏定理）和相似为其基本定理而开展的。其实，平面或空间的坐标化，归根究底其理论基础也就是上述基本定理，解析几何中的距离公式就是毕氏定理；直线的参数式就是相似比的一种表现等等，概括地来说，坐标化乃是对于全平面或全空间有系统地运用定量几何中的基本定理（亦即勾股与相似比），从而把几何的研究转化成代数的一种框架。其实到了十九世纪中叶，Hamilton,Grassmann开始把这种空间结构的代数化做得更加彻底，更加精简，这也就是向量代数。
　　向量代数与空间结构的代数化：空间概念之中，最最原始者首推“位置”，空间本身其实就是所有可能的“位置”的总体。在几何学的讨论中，我们用点来标记一个位置（这也就是为什么有些几何书说空间乃是一个点集）。其次就是由一个位置到另一个位置之间的“通路”。光的存在使得我们体认到空间中两点之间的“最短通路”的唯一存在性，这也就是连接两点之间的“直线段”。这就是空间结构中的最最基本者，它也就是两点之间的“位差”的具体化。直观上一个位差具有方向和距离这样两个要素，例如有人问你：“由这里到某处该如何走？”一个简明扼要的回答就是告诉他两处位差的方向和距离（例如向东北五公里），位移向量（displacement）这个基本概念也就是把方向和距离想象成位差的唯二要素。而且把它想象成一种带有方向成分的代数量，例如向东五公里，向西五公里等等，都是位移向量。换句话说，所有“同向等距的有向线段”都是同一位移向量的具体化，而位移向量则是他们的抽象化。化另外一种确切而生动的说法是：一个向量就是空间的一个“平移”（trauslation）,它把全空间的每一个点都做了一个同向且等距的移动。接着让我们来分析下，两个平移的组合是否还是一个平移呢？设$T_1,T_2$是两个任给的平移，$A,B$是空间任给两点，则有

AT1(A)−→−−−−∥=BT1(B)−→−−−−,

$$\overrightarrow{AT_1(A)}\parallel=\overrightarrow{BT_1(B)},$$ $$\overrightarrow{T_1(A)T_2o T_1(A)}\parallel =\overrightarrow{T_1(B)T_2o T_1(B)}$$ （$\parallel=$表示平行且等长）是否$\overrightarrow{AT_2oT_1(A)}$也和$\overrightarrow{BT_2oT_1(B)}$平行且等长呢？如下图所示

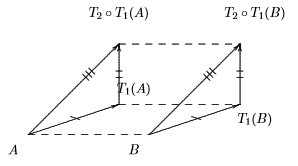
图六

由所设和平行四边形的特征性质，即得$\overrightarrow{AB}\parallel=\overrightarrow{T_1(A)T_1(B)}\parallel=\overrightarrow{T_2oT_1(A)T_2oT_1B}$，因此即得$\overrightarrow{AT_2oT_1(A)}\parallel=\overrightarrow{BT_2oT_1(B)}$。这也就说明了任给两个平移$T_1,T_2$的组合，$T_2oT_1$也必定是一个平移。再者，同样的平行四边形定理也说明$T_2oT_1$和$T_1oT_2$是同一个平移。由此即可自然地引推平移之间的加法运算，即
　　向量加法：$T_1+T_2=T_1oT_2=T_2oT_1=T_2+T_1$
　　由向量加法的复合浓缩，就得到向量的整数倍，即$n\cdot\vec{a}$乃$n$个$\vec{a}$自相加之总和，由此又可以逐步推广而得一个向量的任何有理数倍的和定理,即 $$(-n)\cdot\vec{a}=-(n\cdot\vec{a}).$$ $$n\cdot(\frac{m}{n}\cdot\vec{a})=m\vec{a}$$ 最后，还可以用Eudoxus的逼近原理，把上述向量倍积推广到实数倍，这样所得的向量倍积$k\cdot\vec{a}$的几何描述是：当$k>0$时，$k\cdot\vec{a}$和$\vec{a}$同向而其距离（长度）则是$\left|\vec{a}\right|$的$k$倍，若$k<0$，则$k\cdot\vec{a}$和$\vec{a}$反向而其长度则是$\left|\vec{a}\right|$的$（-k）$倍。再者，容易验证向量倍积具有易算好用的运算律,即

$k_1\cdot(k_2\cdot\vec{a})=(k_1\cdot k_2)\cdot\vec{a}$
$(k_1+k_2)\vec{a}=k_1\vec{a}+k_2\vec{a}$
$k(\vec{a}+\vec{b}=k\vec{a}+k\vec{b})$

若把上述分配律$k(\vec{a}+\vec{b}=k\vec{a}+k\vec{b})$作一图解，即可看出它就是以$\{\vec{a},\vec{b},\vec{a}+\vec{b}\}$为其三边的三角形和以$\{k\vec{a},k\vec{b},k\vec{a}+k\vec{b}\}$为三边的三角形互为相似三角形的代数形式。换句话说，上述分配律乃是原先相似三角形定理的代数化。
　　那么毕氏定理的代数化又是什么呢？若以$\vec{a},\vec{b}$分别表示一个三角形的两个直角边（亦即勾与股），则$\vec{a}+\vec{b}$表示其弦。若以$\left|\vec{a}\right|$表示$\vec{a}$的长度，则勾股弦公式就可以改写成：
　　“当$\vec{a}\bot\vec{b}$时，
　　$\left|\vec{a}+\vec{b}\right|^{2}=\left|\vec{a}\right|^{2}+\left|\vec{b}\right|^{2}=\left|\vec{a}-\vec{b}\right|^{2}$”
在一般情形，$\vec{a}+\vec{b}$和$\vec{a}-\vec{b}$ 是不等长的，它们是一个平行四边形的两条对角线，我们可以把$\vec{b}$分解成$\vec{b_1}+\vec{b_2}$ ，其中$\vec{b_1}$和$\vec{a}$同向（或反向），而$\vec{b_2}$则和$\vec{a}$垂直，如图


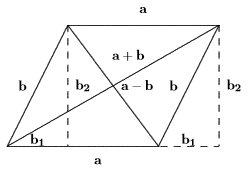
图七

则有：
$$\left|\vec{a}+\vec{b}\right|^{2}+\left|\vec{a}-\vec{b}\right|^{2}\\ =\left|\vec{a}+\vec{b_1}\right|^{2}+\left|\vec{b_2}\right|^{2}+\left|\vec{a}-\vec{b_1}\right|^{2}+\left|\vec{b_2}\right|^{2}\\ =(\left|\vec{a}\right|\pm\left|\vec{b_1}\right|)^{2}+(\left|\vec{a}\right|\mp\left|\vec{b_1}\right|)^{2}+\left|\vec{2b}\right|^{2}\\ =2\left|\vec{a}\right|^{2}+2\left|\vec{b_1}\right|^{2}+2\left|\vec{b_2}\right|^{2}\\ =2\left|\vec{a}\right|^{2}+2\left|\vec{b}\right|^{2}$$
这样，就得出一个对于任意两个向量皆成立的长度关系式，即 $$\left|\vec{a}+\vec{b}\right|^{2}+\left|\vec{a}-\vec{b}\right|^{2}=2\left|\vec{a}\right|^{2}+2\left|\vec{b}\right|^{2}$$ [在$a\bot b$时，图六的平行四边形是个矩形，所以$\|\vec{a}+\vec{b}\|=\|\vec{a}-\vec{b}\|$，上述公式就成为勾股弦公式两边同乘以2。]上述公式通常叫做广义毕氏定理，我们还可以把它进一步推广到对于任给三个向量$\vec{a},\vec{b},\vec{c}$皆成立的一个公式，即为 $$\left|\vec{a}+\vec{b}+\vec{c}\right|^{2}-\left|\vec{a}+\vec{b}\right|^{2}-\left|\vec{b}+\vec{c}\right|^{2}-\left|\vec{c}+\vec{a}\right|^{2}+\left|\vec{a}\right|^{2}+\left|\vec{b}\right|^{2}+\left|\vec{a}\right|^{2}\equiv0　(*)$$ 其推导如下 $$\left|\vec{a}+\vec{b}+\vec{c}\right|^{2}+\left|\vec{a}+\vec{b}-\vec{c}\right|^{2}=2\left|\vec{a}+\vec{b}\right|^{2}+2\left|\vec{c}\right|^{2}　（１）$$ $$\left|\vec{a}-\vec{b}+\vec{c}\right|^{2}+\left|\vec{a}+\vec{b}-\vec{c}\right|^{2}=2\left|\vec{a}\right|^{2}+2\left|\vec{b}-\vec{c}\right|^{2}　（２）$$ $$\left|\vec{a}-\vec{b}+\vec{c}\right|^{2}+\left|\vec{a}+\vec{b}+\vec{c}\right|^{2}=2\left|\vec{a}+\vec{c}\right|^{2}+2\left|\vec{b}\right|^{2}　（３）$$ $$\left|\vec{b}+\vec{c}\right|^{2}+\left|\vec{b}-\vec{c}\right|^{2}=2\left|\vec{b}\right|^{2}+\left|\vec{c}\right|^{2}　　　　　　　（４）$$ $(1)-(2)+(3)-2×(4)$即可得出公式(*)。
这样一个对于任意三个向量皆普遍成立的长度公式看起来的确是十分对称漂亮的，但是它究竟有什么用处呢？这就得略作代数变形才能充分体现其妙用了。若把组合量$\frac{1}{2}\{\left|\vec{a}+\vec{b}\right|^{2}-\left|\vec{a}\right|^{2}-\left|\vec{b}\right|^{2}\}=f(\vec{a},\vec{b})$看成一个定义为一对向量的函数，则(*)一式就变形成上述函数的一个简洁有力的性质，即$2\cdot\{f(\vec{a},\vec{b}+\vec{c})-f(\vec{a},\vec{b})-f(\vec{a},\vec{c})\equiv0\}$，这也就促使我们根本改用符号$\vec{a}\cdot\vec{b}$来表示上述组合量，而且把它想成$\vec{a},\vec{b}$的一种乘积（叫做$\vec{a},\vec{b}$的内积），因为这样就可以把$(*)$一式转变成我们所熟悉惯用的分配律这种形式，
即$\vec{a}\cdot(\vec{b}+\vec{c})=\vec{a}\cdot\vec{b}+\vec{a}\cdot\vec{c}$
（$\vec{a}\cdot\vec{b}=\vec{b}\cdot\vec{a}$是显然的）

由此可见，引用向量内积的妙处是可以把古代的勾股弦现代化成内积分配律这样简洁、易用、有力的代数公式！
　　总结上面这一段讨论，我们就得到整个空间结构的全面代数化，它包括一个基本量：位移向量，三种运算：加、倍积和内积，而他们满足一套极为简便有力的运算律：例如
　　加法交换律：$\vec{a}+\vec{b}=\vec{b}+\vec{a}$（平行四边形定理之代数化）
　　倍积分配律：$k(\vec{a}+\vec{b})=k\vec{a}+k\vec{b}$（相似形定理之代数化）
　　内积分配律：$\vec{a}\cdot(\vec{b}+\vec{c})=\vec{a}\cdot\vec{b}+\vec{a}\cdot\vec{c}$（勾股弦定理之代数化）
　　这种结构叫做向量代数（Vector algebra），它是现代化的解析几何的基础理论，其重要优点是它把定量几何中的基本定理自然地转化成简便有力的分配律，这样，韩信点兵中那种分解组合的想法又可以大展神威了！可以这么说，现代的向量代数乃是把中国古算中的韩信点兵和勾股弦，出入相辅统一起来的数学结构！是几何与代数的一种自然统一！
　　高维勾股定理：上面所讨论的定量几何全面代数化，线性化的另一个重大好处是它给高维勾股定理催生。勾股弦定理是关于长度和角度的基本定理，是否也有关于面积、体积几何量的基本定理呢？这也就是我们所要探讨的高维勾股定理。今天限于时间，只能作一简短介绍如下：
　　在坐标解析几何中，勾股弦定理也就是下述距离公式，即： $$\overline{p_1p_2}^{2}=(x_2-x_1)^{2}+(y_2-y_1)^{2}+(z_2-z_1)^{2}$$ 其几何意义是一条直线段的长度平方等于其在三个正交坐标轴上的垂直投影平方和，类似地，空间一片平面的面积平方是否也等于它在三个（互相垂直的）坐标面上的垂直投影的面积平方和呢？其答案是肯定的，它也就是二维勾股定理的一种初步形式，而其简便好用形式则下述二维有向的内积公式。
　　为了把上述一维向量的内积推广到高维，让我们先对于它的几何意义再做一分析，当$\vec{a},\vec{b}$同向或反向时，容易看到$\vec{a}\cdot\vec{b}=\pm\|\vec{a}\|\cdot\|\vec{b}\|$。所以$\vec{a}\cdot\vec{c}$就是$\vec{a},\vec{b}$的有号长度的乘积，在一般的情形，令$\vec{b'}$为$\vec{b}$在$\vec{a}$的所在直线上的垂直投影，则有$\vec{b}=\vec{b'}+\vec{b''},\vec{b''}\bot\vec{a}$（如图八所示）
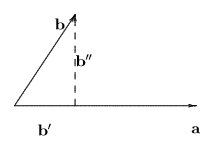
图八

$$\vec{a}\cdot\vec{b}=\vec{a}(\vec{b'}+\vec{b''})=\vec{a}\cdot\vec{b'}=\pm\|\vec{a}\|\|\vec{b'}\|,$$ $$\vec{a}\cdot\vec{b''}=0。$$ 在二维的情形，我们可以把一个平行四边形想成是一种基本的二维有向量，用符号∥$(\vec{a},\vec{b})$表示由两个一维向量$\vec{a},\vec{b}$所张的平行四边形，用符号∥$(\vec{a},\vec{b})$表示由两个一维向量$\vec{a},\vec{b}$所张的平行四边形，用Ã$(\vec{a},\vec{b})$表示其面积，则不难看到Ã$(\vec{a},\vec{b})$满足下列基本性质，即
（$\checkⅰ$）对称性：Ã$(\vec{a},\vec{b})$=Ã$(\vec{b},\vec{a})$
（$\checkⅱ$）剪应不变性（Shearing Invariance）：Ã$(\vec{a},\vec{b}+k\vec{a})$=Ã$(\vec{a},\vec{b})$
（$\checkⅲ$）Ã$(k\vec{a},\vec{b})=\|k\|$Ã$(\vec{a},\vec{b})$
因为Ã恒为正值，所以（ⅲ）一式中的$\|k\|$是必然的，一如$\|k\vec{a}\|=\|k\|\cdot\|\vec{a}\|$。但是这个“加绝对值”的等式，往后用起来是会产生诸多不便的。所以若有可能，我们得设法避免之（即改善之）。一个自然的出路是给平面和其上的平行四边形都加以定向(Orientation)：若由$\vec{a}$到$\vec{b}$的转角和平面上的“正向转角”同向，则定义∥$(\vec{a},\vec{b})$的有号面积为正，反之，若两者异向，则定义∥$(\vec{a},\vec{b})$的有号面积为负，亦即有号面积$A(\vec{a},\vec{b })=\pm$Ã$(k\vec{a},\vec{b})$,而$\pm$号由两者同向或异向而定，则有
（ⅰ）斜对称性：$A(\vec{a},\vec{b})=-A(\vec{b},\vec{a})$
（ⅱ）剪应不变性：$A(\vec{a},\vec{b}+k\vec{a})=A(\vec{a},\vec{b})$
（ⅲ）$A(k\vec{a},\vec{b})=\|k\|A(\vec{a},\vec{b})$
将$A(\vec{a},\vec{b})$和原先的Ã$(\vec{a},\vec{b})$做一比较，骤看起来似乎互有长短:（$\checkⅰ$）略胜（ⅰ）一筹；而（ⅲ）略胜（$\checkⅲ$）一筹。其实进一步的分析就可以由（ⅰ）（ⅱ）（ⅲ）推导而得下列有号面积函数的分配律（亦即双线性）：
（ⅳ）$A(\vec{a},\vec{b}+\vec{c})=A(\vec{a},\vec{b})+A(\vec{a},\vec{b})$
所以$A(\vec{a},\vec{b})$其实是远优于Ã$(\vec{a},\vec{b})$的！这也就是我们要采用有号面积的道理，现在我们就可以用有号面积和垂直投影来同样的定义空间中任给两个平行四边形//$(\vec{a},\vec{b})$和//$(\vec{c},\vec{d})$的“内积”了，先看两者共在一平面上的情形，自然可以把两者的内积定义为它们的有号面积的乘积，亦即//$(\vec{a},\vec{b})$，//$(\vec{c},\vec{d})$共面时，$//(\vec{a},\vec{b})\cdot//(\vec{c},\vec{d})=A(\vec{a},\vec{b})\cdot A(\vec{c},\vec{d})$。在一般的情形，令$c',d'$为$c,d$在$//(\vec{a},\vec{b})$所在平面上的垂直投影，则可以仿照一维内积的情形作下述定义：$//(\vec{a},\vec{b})\cdot//(\vec{c},\vec{d})=//(\vec{a},\vec{b})\cdot//(\vec{c'},\vec{d'})=A(\vec{a},\vec{b})\cdot A(\vec{c'},\vec{d'})$。
二维勾股定理： $$//(\vec{a},\vec{b})\cdot//(\vec{c},\vec{d})= \begin{array}{|cc|} \vec{a}\cdot\vec{b}, &\vec{b}\cdot\vec{c}\\ \vec{a}\cdot\vec{d},&\vec{b}\cdot\vec{d}\\ \end{array}$$ 由上述把二维内积转化成一维内积来计算的公式，可以看到它是对于$\vec{a},\vec{b},\vec{c},\vec{d}$都是线性的，亦即满足分配律的！
　　证明：先证两者共面的情形，令$\vec{e_1},\vec{e_2}$是在该平面上的一组正交基。由有号面积的双线性和斜对称性容易得出 $$A(\vec{a},\vec{b})=\begin{array}{|cc|} \vec{a}\cdot\vec{e_1}, &\vec{b}\cdot\vec{e_1}\\ \vec{a}\cdot\vec{e_2},&\vec{b}\cdot\vec{e_2}\\ \end{array}$$ , $$A(\vec{c},\vec{d})=\begin{array}{|cc|} \vec{c}\cdot\vec{e_1}, &\vec{d}\cdot\vec{e_1}\\ \vec{c}\cdot\vec{e_2},&\vec{d}\cdot\vec{e_2}\\ \end{array}$$ 所以由上述二维内积的定义，即有 $$//(\vec{a},\vec{b})\cdot//(\vec{c},\vec{d})=\begin{array}{|cc|} \vec{a}\cdot\vec{e_1}, &\vec{b}\cdot\vec{e_1}\\ \vec{a}\cdot\vec{e_2},&\vec{b}\cdot\vec{e_2}\\ \end{array}\cdot\begin{array}{|cc|} \vec{c}\cdot\vec{e_1}, &\vec{d}\cdot\vec{e_1}\\ \vec{c}\cdot\vec{e_2},&\vec{d}\cdot\vec{e_2}\\ \end{array}=\begin{array}{|cc|} \vec{a}\cdot\vec{c}, &\vec{b}\cdot\vec{c}\\ \vec{a}\cdot\vec{d},&\vec{b}\cdot\vec{d}\\ \end{array}$$ [上述第二个等式是代数恒等式，请读者自行验算之。]
　　在一般的情形，令$c',d'$为$c,d$在$//(\vec{a},\vec{b})$所在平面上的垂直投影，则有 $$\vec{a}\cdot\vec{c'}=\vec{a}\cdot\vec{c},\vec{b}\cdot\vec{c'}=\vec{b}\cdot\vec{c}$$ $$\vec{a}\cdot\vec{d'}=\vec{a}\cdot\vec{d},\vec{b}\cdot\vec{d'}=\vec{b}\cdot\vec{d}$$ 再由二维内积的定义即得 $$//(\vec{a},\vec{b})\cdot//(\vec{c},\vec{d})=A(\vec{a},\vec{b})\cdot A(\vec{c'},\vec{d'})=\begin{array}{|cc|} \vec{a}\cdot\vec{c'}, &\vec{b}\cdot\vec{c'}\\ \vec{a}\cdot\vec{d'},&\vec{b}\cdot\vec{d'}\\ \end{array}=\begin{array}{|cc|} \vec{a}\cdot\vec{c}, &\vec{b}\cdot\vec{c}\\ \vec{a}\cdot\vec{d},&\vec{b}\cdot\vec{d}\\ \end{array}$$ 今天限于时间，不能对于上述二维勾股弦定理以及其高维推广作一有系统地讨论。总之，高维勾股弦定理依然是以高维内积的分配律这种极为简便有力的形式出现，唯有有了他们，高维定量几何的基础理论才真正达到完善的至精至简境界。另外一个耐人寻味的数学史上的事实是由一维勾股弦到二维勾股弦这个过程竟长达两千余年，可见真正基本而重要的进展，是得来不易的！而其最后，则又是以简便有力的内积分配律一以贯之！
　　分配律的威力由韩信点兵启蒙，一直到近代力学和量子力学，可以说无往不利，这种朴素的线性组合的妙用，既广且深，贯穿全局，充分地体现了基础数学中的至精至简。今天且以下述四句话，给基础数学的基本精神和进化历程做一个还算确切的描述，那就是：
　　
返璞归真，精益求精，至精至简，以简御繁。

---

*参考文献：项武义香港大学及国立中央大学公开演讲