算法系列—分治法

关键字：相同子问题、递归、合并

一、基本概念：

     所谓分治法是指， 把一个复杂的问题分成两个或更多的相同或相似的子问题，再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解，原问题的解即子问题的解的合并。这个技巧是很多高效算法的基础，如排序算法(快速排序，归并排序)，傅立叶变换(快速傅立叶变换)……

二、算法思想和策略：

    分治法的设计思想是：将一个难以直接解决的大问题，分割成一些规模较小的相同问题，以便各个击破，分而治之。

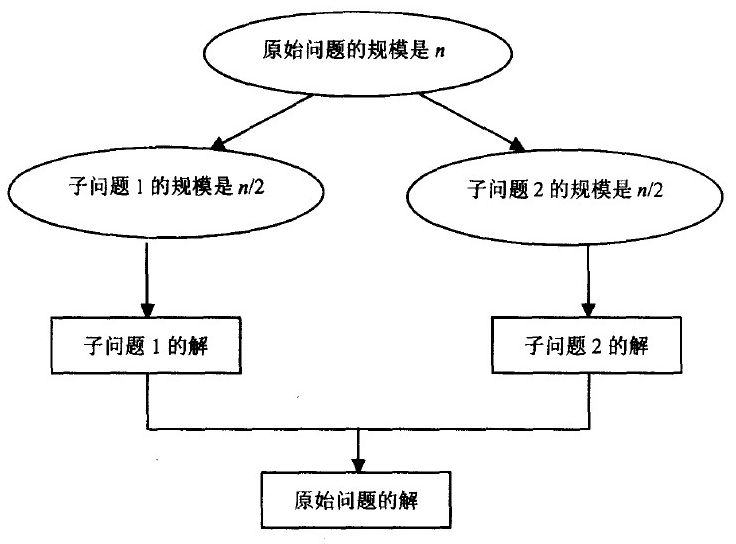
    分治策略是：对于一个规模为n的问题，若该问题可以容易地解决（比如说规模n较小）则直接解决，否则将其分解为k个规模较小的子问题，这些子问题互相独立且与原问题形式相同，递归地解这些子问题，然后将各子问题的解合并得到原问题的解。这种算法设计策略叫做分治法。

    如果原问题可分割成k个子问题，1<k≤n，且这些子问题都可解并可利用这些子问题的解求出原问题的解，那么这种分治法就是可行的。由分治法产生的子问题往往是原问题的较小模式，这就为使用递归技术提供了方便。在这种情况下，反复应用分治手段，可以使子问题与原问题类型一致而其规模却不断缩小，最终使子问题缩小到很容易直接求出其解。这自然导致递归过程的产生。分治与递归像一对孪生兄弟，经常同时应用在算法设计之中，并由此产生许多高效算法。

三、算法特点和适用情况：    

    分治法所能解决的问题一般具有以下几个特征：

      1.该问题的规模缩小到一定的程度就可以容易地解决

      2.该问题可以分解为若干个规模较小的相同问题，即该问题具有最优子结构性质。

      3.利用该问题分解出的子问题的解可以合并为该问题的解；

      4.该问题所分解出的各个子问题是相互独立的，即子问题之间不包含公共的子子问题。

    第一条特征是绝大多数问题都可以满足的，因为问题的计算复杂性一般是随着问题规模的增加而增加；

    第二条特征是应用分治法的前提它也是大多数问题可以满足的，此特征反映了递归思想的应用；、

    第三条特征是关键，能否利用分治法完全取决于问题是否具有第三条特征，如果具备了第一条和第二条特征，而不具备第三条特征，则可以考虑用贪心法或动态规划法。

    第四条特征涉及到分治法的效率，如果各子问题是不独立的则分治法要做许多不必要的工作，重复地解公共的子问题，此时虽然可用分治法，但一般用动态规划法较好。

四、分治法的实现步骤

    分治法在每一层递归上都有三个步骤：

      1.分解：将原问题分解为若干个规模较小，相互独立，与原问题形式相同的子问题；

      2.解决：若子问题规模较小而容易被解决则直接解，否则递归地解各个子问题；

      3.合并：将各个子问题的解合并为原问题的解。

    依据分治法设计程序时，实际上就是类似于数学归纳法，找到解决本问题的求解方程公式，然后根据方程公式设计递归程序。

      1.一定是先找到最小问题规模时的求解方法；

      2.然后考虑随着问题规模增大时的求解方法；

      3.找到求解的递归函数式后（各种规模或因子），设计递归程序即可。

  

五、实例分析

    分治法可以求解很多问题，比如二分搜索、大整数乘法、Strassen矩阵乘法、棋盘覆盖、合并排序、快速排序、线性时间选择、最接近点对问题、循环赛日程表、汉诺塔等，现就著名的棋盘覆盖问题，采用分治法分析之。

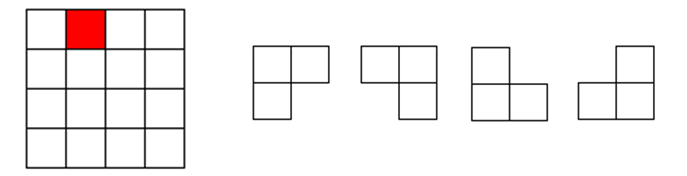
   问题描述：在一个2^k * 2^k个方格组成的棋盘中，恰有一个方格与其它方格不同，称该方格为一特殊方格，且称该棋盘为以特殊棋盘。在棋盘覆盖问题中，要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格之外的所有方格，且任何2个L型骨牌不得重叠覆盖。

   算法分析思路： 当k>0时，将2^k * 2^k棋盘分割为4个2^(k-1) * 2^(k - 1)子棋盘，如下图所示。特殊方格必位于4个较小子棋盘之一种，其余3个子棋盘中无特殊方格。为了将这3个无特殊方格的子棋盘转化为特殊棋盘，可以用一个L型骨牌覆盖这3个较小棋盘的会合处，如下图所示。从而将原问题转化为4个较小规模的棋盘覆盖问题。递归地使用这种分割，直至棋盘简化为棋盘1*1。（部分转载）

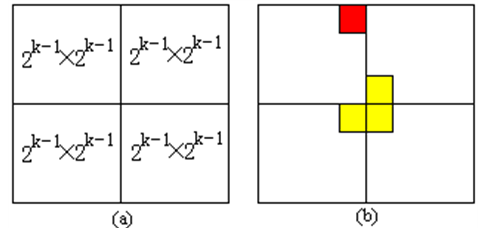
     将2^k * 2^k的棋盘，先分成相等的四块子棋盘，其中特殊方格位于四个中的一个，构造剩下没特殊方格的三个字棋盘，将它们中的也假设一个方格为特殊方格。如果是：

       左上角的子棋盘（若不存在特殊方格）：则将该子棋盘右下角的那个方格假设为特殊方格；

    右上角的子棋盘（若不存在特殊方格）：则将该子棋盘左下角的那个方格假设为特殊方格；

    左下角的子棋盘（若不存在特殊方格）：则将该子棋盘右上角的那个方格假设为特殊方格；

    右下角的子棋盘（若不存在特殊方格）：则将该子棋盘左上角的那个方格假设为特殊方格；

    当然，上面四种情况，只可能且必定只有三种成立，那三个假设的特殊方格刚好构成一个L型骨牌，我们可以给它们作上相同的标志。这样四个子棋盘就分别都和原来的大棋盘类似，我们就可以用递归的算法解决了。

   算法实现：算法C++语言描述如下：

    #include <stdio.h>
    #include <stdlib.h>

    #define SIZE 4

    static int title = 1;    //title表示L型骨牌的编号
    static int board[SIZE][SIZE];

    /**
     * 功能：棋盘覆盖
     * @param tr表示棋盘左上角行号
     * @param tc表示棋盘左上角列号
     * @param dr表示特殊棋盘的行号
     * @param dc表示特殊棋盘的列号
     * @param size = 2^k
     * 棋盘的规格为2^k * 2^k
     **/
     void ChessBoard(int tr, int tc, int dr, int dc, int size)
     {
         if(1 == size)
         {
             return;
         }
        
         int t = title++;    //L型骨牌号
         int s = size / 2;    //分割棋盘
        
         //覆盖左上角子棋盘
         if(dr < tr + s && dc < tc + s)
         {
             //特殊方格在此棋盘中
             ChessBoard(tr, tc, dr, dc, s);
         }
         else
         {
             //此棋盘无特殊方格
             //用t号L型骨牌覆盖右下角
             board[tr + s - 1][tc + s - 1] = t;
             //覆盖其余方格
             ChessBoard(tr, tc, tr + s - 1, tc + s - 1, s);
         }

         //覆盖右上角
         if(dr < tr + s && dc >= tc + s)
         {
             //特殊方格在此棋盘中
             ChessBoard(tr, tc + s, dr, dc, s);
         }
         else
         {
             //此子棋盘中无特殊方格
             //用t号L型骨牌覆盖左下角
             board[tr + s - 1][tc + s] = t;
             //覆盖其余方格
             ChessBoard(tr, tc + s, tr + s - 1, tc + s, s);
         }
        
         //覆盖左下角子棋盘
         if(dr >= tr + s && dc < tc + s)
         {
             //特殊方格在此棋盘中
             ChessBoard(tr + s, tc, dr, dc, s);
         }
         else
         {
             //用t号L型骨牌覆盖右上角
             board[tr + s][tc + s -1] = t;
             //覆盖其余方格
             ChessBoard(tr + s, tc, tr + s, tc + s - 1, s);
         }

         //覆盖右下角子棋盘
         if(dr >= tr + s && dc >= tc + s)
         {
             //特殊方格在此棋盘中
             ChessBoard(tr + s, tc + s, dr, dc, s);
         }
         else
         {
             //用t号L型骨牌覆盖左上角
             board[tr + s][tc + s] = t;
             //覆盖其余方格
             ChessBoard(tr + s, tc + s, tr + s, tc + s, s);
         }
    }

    //打印
    void ChessPrint()
    {
        int i;
        int j;
        for(i = 0; i < SIZE; i++)
        {
            for(j = 0; j < SIZE; j++)
            {
                printf("%d ", board[i][j]);
            }
            printf("n");
        }
    }

    int main(int argc, char **argv)
    {
        //方便测试，假设特殊方格位置在第三行第三列
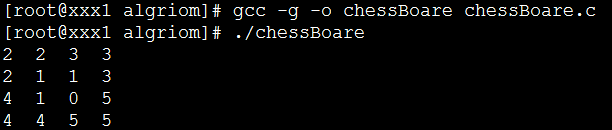
        ChessBoard(0, 0, 2, 2, SIZE);
        ChessPrint();
        return 0;
    }

   结果如下：

转载请注明出处：http://blog.csdn.net/daijin888888/article/details/53113831