转自https://www.shuxuele.com/algebra/polynomials-division-long.html
多项式长除法
多项式看起来像这样:
 |
| 多项式例子 这个多项式有 3 项 |
除法
有时候可以这样做多项式除法。
但有时用 "长除" 会比较合适(与数字长除法相似)
分子和分母
每部分的多项式有都有名字:
- 上面的多项式叫分子
- 下面的多项式叫分母
来帮你记住,想象:妈妈抱着孩子在身体上面。
方法
多项式长除
整整齐齐的写下来:
- 先写分母,
- 然后在右边写 ")",
- 再写分子,上面画一条线
两个多项式的项都要"以从大到小的次数排列"(大指数――像 x2 里的 "2"――的项放在前面)。
然后:
 |
|
| 用这新的多项式重复以上的运算 |
例解会比较清楚!
例子:
![]()
整齐地写下来,如下,然后逐步去解(按 play):
检测答案:
把答案乘以下面的多项式,结果应该是上面的多项式:
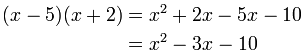
![]()
余项
上面的例子刚好可以整除,但并不是时常都这样!看看这个:
做完以后还剩下 "2",这便是 "余项"。
余项是除完之后剩下的项。
但我们还是得到了答案:把余项除以下面的多项式写在旁边作为答案的一部分,像这样:
![]()
"缺"項
多项式里可能有"空缺的項"(例子:可能有 x3,但 没有 x2)。如是这样,你可以留下空格,或写下系数为零的缺項。
例子:
![]()
写下以 "0" 为缺項的系数,然后照以上的步骤去解(按 play):
看到在 "3x3" 的位置我们放了一个空格吗?
多元(多于一个变量)
上面讲的是一元多项式――只有一个变量(x)――的除法,但同样的方法也适用于多元多项式――多于一个变量(例如 x 和 y)。
例子:
![]()








 本文介绍了多项式长除法的基本概念及操作步骤,包括如何进行有序书写、分子和分母的定义、具体的操作方法以及如何处理余项和缺項的情况,并通过实例详细展示了整个过程。
本文介绍了多项式长除法的基本概念及操作步骤,包括如何进行有序书写、分子和分母的定义、具体的操作方法以及如何处理余项和缺項的情况,并通过实例详细展示了整个过程。



















 1472
1472

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








