#include <stdio.h>
int main()
{
float r;
int n;
int x;
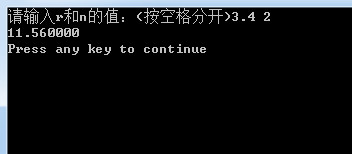
printf("请输入r和n的值:(按空格分开)");
scanf("%f %d",&r,&n);
for(x=1;x<n;x++)
{
r=r*r;
}
printf("%f\n",r);
return 0;
}
#include <stdio.h>
int main()
{
float r;
int n;
int x;
printf("请输入r和n的值:(按空格分开)");
scanf("%f %d",&r,&n);
for(x=1;x<n;x++)
{
r=r*r;
}
printf("%f\n",r);
return 0;
}

 1702
1702
 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


