三次参数样条曲线与Cardinal曲线

荆楚闲人

已于 2023-10-19 16:24:41 修改

阅读量551

点赞数 3

分类专栏：数学理论文章标签：算法 Cardinal曲线 Hermite基矩阵

于 2023-10-16 11:15:35 首次发布

数学理论专栏收录该内容

11 篇文章 0 订阅

订阅专栏

1. 三次参数样条曲线

三次样条曲线的唯一缺点就是缺乏几何不变形。即当型值点发生几何变换时不能保证参数递增。因此提出了以弦长为参数的三次参数样条曲线。

1.1. 定义

已知n个型值点Pi(xi, yi), i = 1, 2,…, n且相邻型值点不重合；若 p(t) 满足下列条件：

型值点Pi在函数 p(t) 上。
p(t) 在整个区间[P1, Pn]上二阶连续可导。
在每个子区间[Pi, Pi+1], i = 1, 2,…, n-1上，分段函数 p(t) 都是参数t的三次多项式。则称函数是过型值点的三次参数样条函数，由三次参数样条函数构成的曲线称为三次参数样条曲线。

其中，

子区间的弦长Li为：

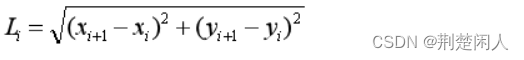
1.2 表达式

第i段的 pi(t) 表示为：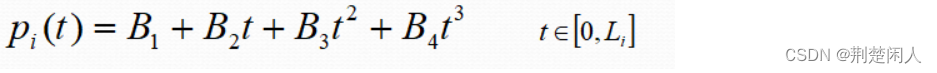

总的来说，三次参数样条曲线就是在三次样条曲线基础上对xyz各分量分别进行参数化的曲线表达，如下：

3个坐标分量x，y，z分别是参数 t 的三次样条函数。
对型值点做参数化。
对3个坐标分量分别处理。

1.3 算法

（1）读入n个型值点坐标。
（2）根据实际情况，确定三次参数样条曲线的边界条件。
（3）计算曲线的系数，将其表达为型值点二阶导数的函数。
（4）用追赶法分别沿x方向与y方向求解三弯矩方程。
（5）将求解出的系数代入三次参数样条函数的x分量与y分量表达式中，构造三次参数样条曲线。
（6）循环访问每个节点。在每个子区间内，参数t按照弦长计算增量，根据每组（x，y）坐标，绘制三次参数样条曲线。

1.4 代码实现

1.4.1 读取型值点

首先我们需要来扩充以下二维点类p2.h与p2.cpp(主要如下)：

class CP2  
{
public:
	CP2();
	virtual ~CP2();
	CP2(double x, double y);
	friend CP2 operator +(const CP2 &p0, const CP2 &p1);//运算符重载
	friend CP2 operator -(const CP2 &p0, const CP2 &p1);
	friend CP2 operator -(double scalar, const CP2 &p);
	friend CP2 operator -(const CP2 &p, double scalar);
	friend CP2 operator *(const CP2 &p, double scalar);
	friend CP2 operator *(double scalar, const CP2 &p);
	friend CP2 operator /(const CP2 &p0, CP2 &p1);
	friend CP2 operator /(const CP2 &p, double scalar);
public:
	double x;//直线段端点x坐标
	double y;//直线段端点y坐标
};

CP2::CP2()
{

}

CP2::~CP2()
{

}

CP2::CP2(double x, double y)
{
	this->x = x;
	this->y = y;
}

CP2 operator +(const CP2 &p0, const CP2 &p1)//对象的和
{
	CP2 result;
	result.x = p0.x + p1.x;
	result.y = p0.y + p1.y;
	return result;
}

CP2 operator -(const CP2 &p0, const CP2 &p1)//对象的差
{
	CP2 result;
	result.x = p0.x - p1.x;
	result.y = p0.y - p1.y;
	return result;
}
CP2 operator -(double scalar, const CP2 &p)//常量和对象的差
{
	CP2 result;
	result.x = scalar - p.x;
	result.y = scalar - p.y;
	return result;
}
CP2 operator -(const CP2 &p, double scalar)//对象和常量的差
{
	CP2 result;
	result.x = p.x - scalar;
	result.y = p.y - scalar;
	return result;
}

CP2 operator *(const CP2 &p, double scalar)//对象和常量的积
{
	return CP2(p.x * scalar, p.y * scalar);
}

CP2 operator *(double scalar, const CP2 &p)//常量和对象的积
{	
	return CP2(p.x * scalar, p.y * scalar);
}

CP2 operator /(const CP2 &p0, CP2 &p1)//对象的商
{
	if(fabs(p1.x)<1e-6)
		p1.x = 1.0;
	if(fabs(p1.y)<1e-6)
		p1.y = 1.0;
	CP2 result;
	result.x = p0.x / p1.x;
	result.y = p0.y / p1.y;
	return result;
}

CP2 operator /(const CP2 &p, double scalar)//对象数除
{
	if(fabs(scalar)<1e-6)
		scalar = 1.0;
	CP2 result;
	result.x = p.x / scalar;
	result.y = p.y / scalar;
	return result;
}

之后在主函数中定义读取函数：

// CGeometricfiguretestViewmessage handlers
void CGeometricfiguretestView::ReadPoint()
{
	P[1].x = -400, P[1].y = -150;
	P[2].x = -100, P[2].y =  0;
	P[3].x = -300, P[3].y =  100;
	P[4].x =  0,   P[4].y =  200;
	P[5].x =  300, P[5].y =  100;
	P[6].x =  100, P[6].y =  0;
	P[7].x =  400, P[7].y =  -150;
}

1.4.2 绘制型值点

//绘制型值点
void CGeometricfiguretestView::DrawDataPoint(CDC* pDC)
{
	CBrush NewBrush, *OldBrush;
	NewBrush.CreateSolidBrush(RGB(0, 0, 0));
	OldBrush = pDC->SelectObject(&NewBrush);
	for(int i = 1; i < 8; i++)
		pDC->Ellipse(ROUND(P[i].x - 5), ROUND(P[i].y - 5), ROUND(P[i].x + 5), ROUND(P[i].y + 5));
	pDC->SelectObject(OldBrush);
}

1.4.3 三次参数样条曲线绘制

三次参数样条曲线计算与绘制，具体过程见注释(计算与推导和三次样条曲线致)：

//三次参数样条曲线
void CGeometricfiguretestView::DrawCubicSpline(CDC* pDC)
{
	int n = 7;
	const int dim = 8;//二维数组维数
	double b1 = 0, bn = 0;//起点和终点的一阶导数
	double L[dim];//参数样条曲线的弦长
	double lambda[dim], mu[dim];
	double l[dim], m[dim], u[dim];
	CP2 c1, cn;//起点和终点的方向余弦
	CP2	D[dim];
    CP2 M[dim], K[dim];//追赶法过渡矩阵
    CP2 B1[dim], B2[dim], B3[dim], B4[dim];//函数的系数
	CP2 delt[dim];
	for(int i=1; i<n;i++)//计算弦长
    {
		delt[i]=P[i+1]-P[i];
		L[i]=sqrt(delt[i].x*delt[i].x+delt[i].y*delt[i].y);
	}
	//边界条件的投影
    c1.x = b1*cos(delt[1].x/L[1]);//起点
	c1.y = b1*cos(delt[1].y/L[1]);
   	cn.x = bn*cos(delt[n-1].x/L[n-1]);//终点
	cn.y = bn*cos(delt[n-1].y/L[n-1]);
	for(int i = 2; i < n; i++)
	{
		lambda[i] = L[i-1]/(L[i-1]+L[i]);//计算λ
		mu[i]=L[i]/(L[i-1]+L[i]);//计算μ
		D[i]=6/(L[i-1]+L[i])*((P[i+1]-P[i])/L[i]-(P[i]-P[i-1])/L[i-1]);//计算D
    }
	D[1]=6*((P[2]-P[1])/L[1]-b1)/L[1];//夹持端的D[1]
    D[n]=6*(bn-(P[n]-P[n-1])/L[n-1])/L[n-1];//夹持端的D[n]
    mu[1]=1;//夹持端的μ[1],
	lambda[n]=1;//夹持端的λ[n]
	//追赶法求解三弯矩方程
    l[1]=2;
	u[1]=mu[1]/l[1];
    for(int i=2; i <= n; i++)
    {
		m[i]=lambda[i];
        l[i]=2-m[i]*u[i-1];
        u[i]=mu[i]/l[i];
    }
    K[1] = D[1]/l[1];//解LK=D
    for(int i = 2; i <= n;i++)
    {
		K[i]=(D[i]-m[i]*K[i-1])/l[i];
	}
	M[n] = K[n];//解UM=K
	for(int i = n-1; i >= 1;i--)
	{
		M[i]=K[i]-u[i]*M[i+1];
	}
	//计算三次样条函数的系数
	for(int i = 1; i < n; i++)
    {
		B1[i]=P[i];
        B2[i]=(P[i+1]-P[i])/L[i]-L[i]*(M[i]/3+M[i+1]/6);
        B3[i]=M[i]/2;
        B4[i]=(M[i+1]-M[i])/(6*L[i]);
    }
	CPen pen(PS_SOLID,3,RGB(0,0,0));
	pDC->SelectObject(&pen);
	pDC->MoveTo(ROUND(P[1].x), ROUND(P[1].y));
	double tStep = 0.5;//步长
	CP2 p;
	for(int i = 1; i < n; i++)//循环访问每个节点
    {
		for(double t=0; t <= L[i]; t += tStep)
		{
			p =B1[i]+B2[i]*t+B3[i]*t*t+B4[i]*t*t*t;
			pDC->LineTo(ROUND(p.x), ROUND(p.y));//绘制参数样条曲线
        }
    }

1.4.4 主函数调用

void CGeometricfiguretestView::OnDraw(CDC* pDC)
{
	CTestDoc* pDoc = GetDocument();
	ASSERT_VALID(pDoc);
	if (!pDoc)
		return;
	// TODO: add draw code for native data here
	CRect rect;//定义客户区矩形
	GetClientRect(&rect);//获得客户区矩形的信息
	pDC->SetMapMode(MM_ANISOTROPIC);//自定义二维坐标系
	pDC->SetWindowExt(rect.Width(), rect.Height());//设置窗口范围
	pDC->SetViewportExt(rect.Width(), -rect.Height());//设置视区范围，且x轴水平向右为正，y轴垂直向上为正
	pDC->SetViewportOrg(rect.Width() / 2, rect.Height() / 2);//设置客户区中心为二维坐标系原点
	rect.OffsetRect(-rect.Width() / 2, -rect.Height() / 2);//rect矩形与客户区重合
	ReadPoint();
	DrawDataPoint(pDC);
	DrawCubicParameterSpline(pDC);
}

编译运行，可见如下：

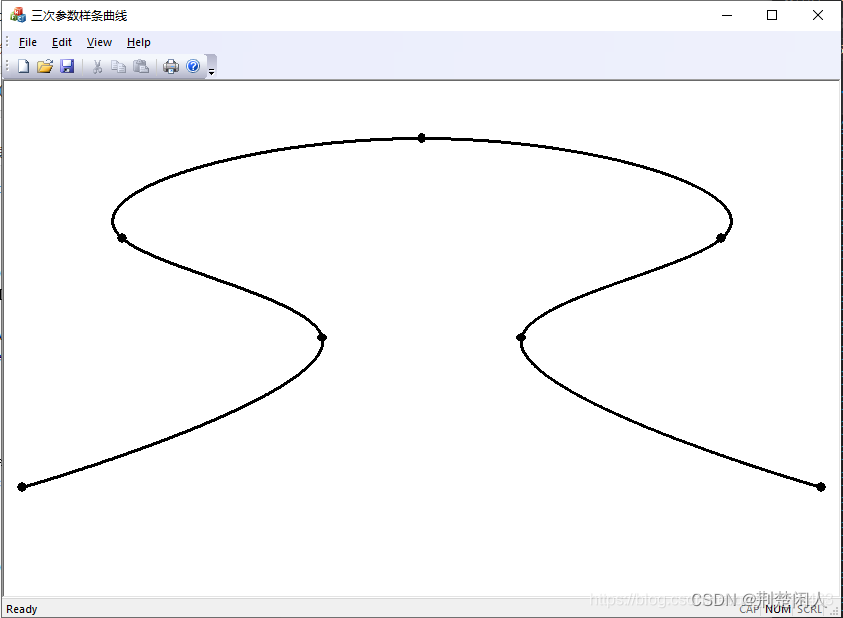
我们也可以改变一下边界约束条件：

double b1 = 1, bn = 1;//起点和终点的一阶导数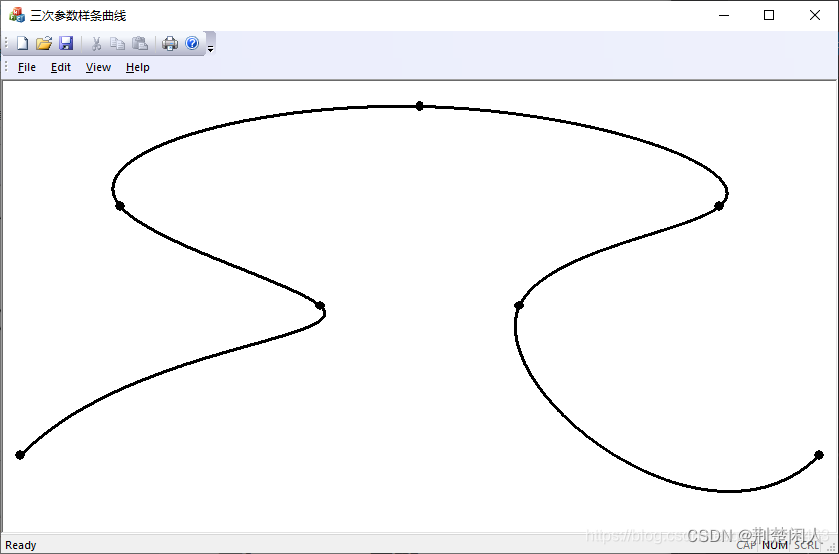

2. Cardinal曲线

2.1 Hermite基矩阵

Hermite的每个曲线两个端点的坐标和导数来定义。

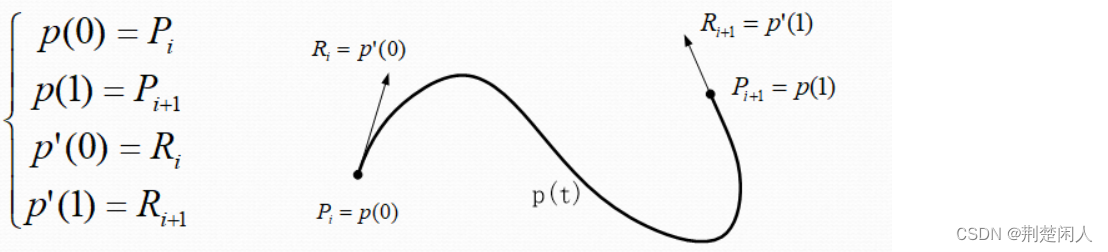假设Hermite样条曲线的方程可以写成矩阵形式，如下：

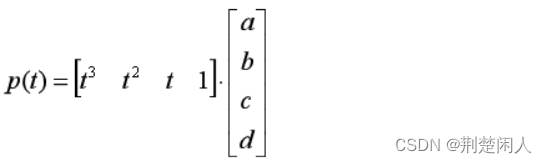
将边界条件p(0)=yi和p(1)=yi+1代入上式，得：

且上式的一阶导数为：

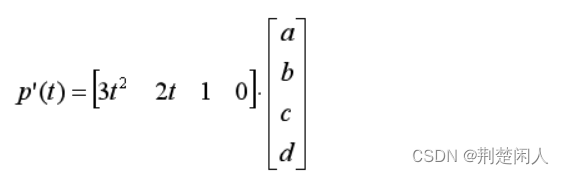
将边界条件p’(0)=Ri和p’(1)=Ri+1带入上式，得：

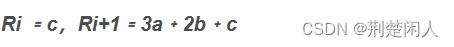
Hermite边界条件的矩阵表示为：

该方程对多项式系数求解，有：

式中，Mh称为Hermite基矩阵，是边界约束矩阵的逆矩阵。需要说明的是，弗格森于1963年用于飞机设计的均匀参数插值三次样条方程就是Mh。

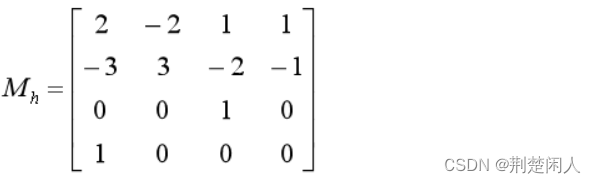
因此，可得：

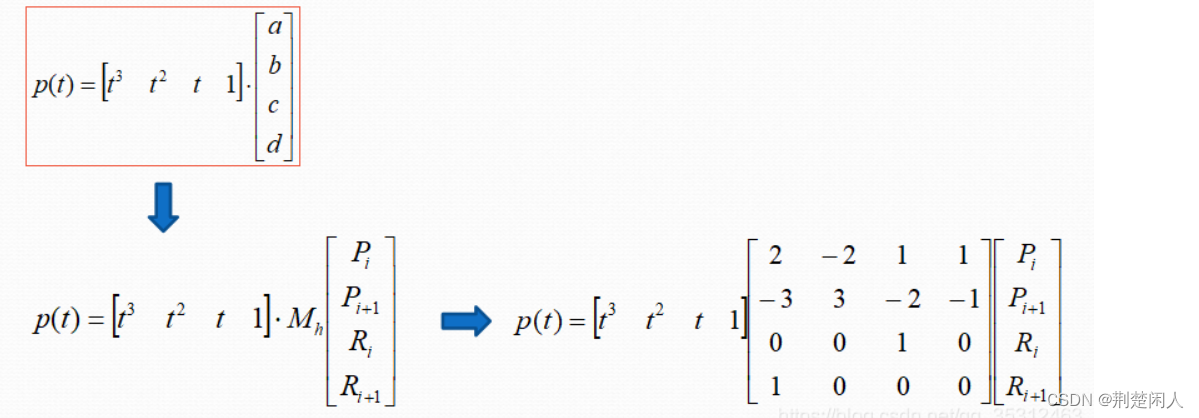
最终可得到：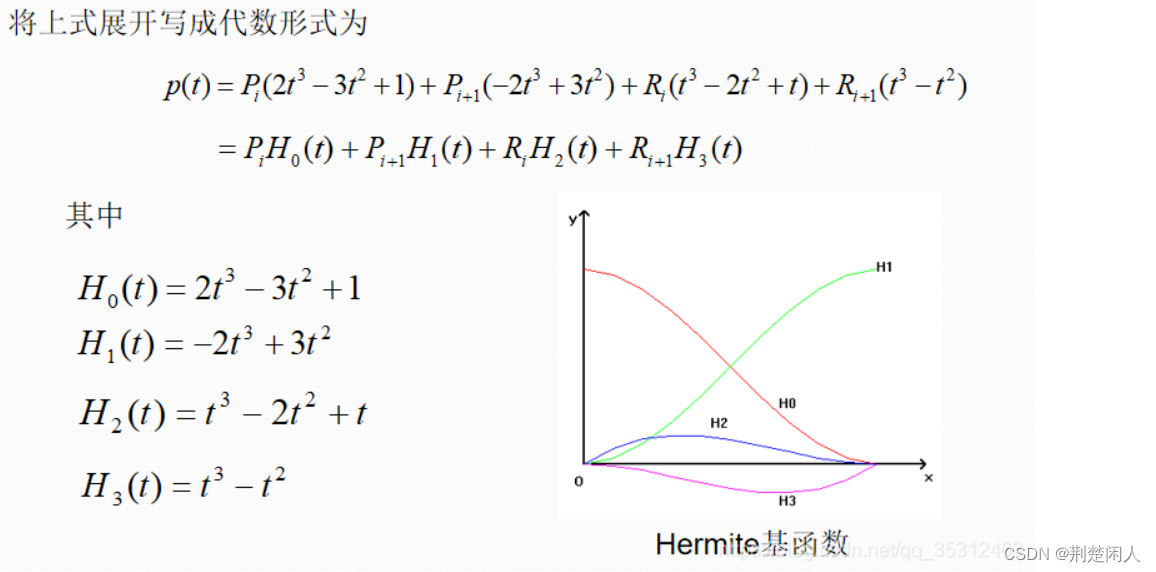

2.2 Cardinal曲线

Cardinal样条是Hermite样条的变形，仅由相邻型值点的坐标就可以计算出导数。设相邻的四个型值点分别记为Pi-1, Pi, Pi+1,Pi+2。Cardinal样条插值方法规定Pi, Pi+1两型值点间插值多项式的边界条件为：

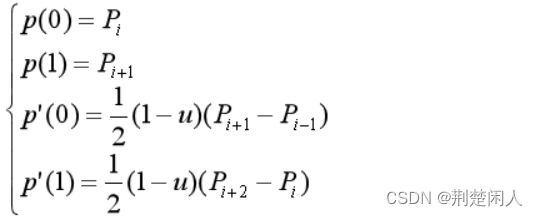
式中, u为可调参数,称为张力参数,可以控制Cardinal样条曲线型值点间的松紧程度。
记s=(1-u)/2,用类似Hermite曲线样条中的方法,将Cardinal边界条件代入下边的参数方程,

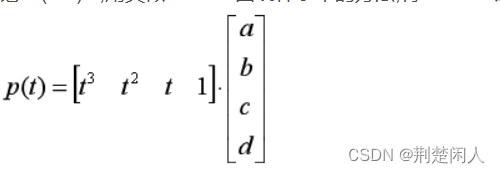
可以得到矩阵表达式：

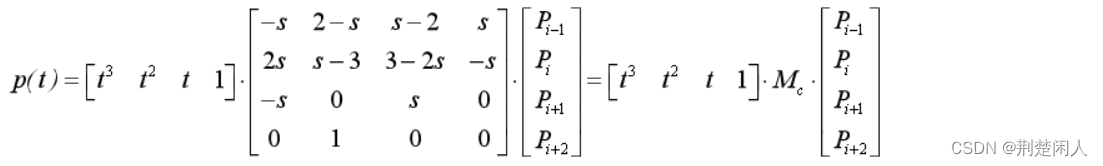
式中，Mc称为Cardinal矩阵。

一条Cardinal样条曲线完全由四个连续的型值点给出，中间两个型值点是曲线段端点，另外两个型值点用来辅助计算端点导数。只要给出一组型值点的坐标值，就可以分段绘制出Cardinal样条曲线。

2.3 Cardinal 算法

（1）读入n个型值点坐标Pi，i=1,2，…n。
（2）在两端各加入一个虚拟点P0和Pn+1。
（3）设置张力参数u值，计算Cardinal基矩阵Mc。
（4）计算Mc矩阵与边界条件矩阵的算法，每4个顶点构成一个条件矩阵。
（5）根据型值点个数计算每段曲线中插值参数t的值，使用直线段连接对应的点p(x(t)，y(t))绘制曲线。

2.4 代码实现

2.4.1 读取型值点

void CGeometricfiguretestView::ReadPoint()
{
	P[0].x =-500, P[0].y =0;
	P[1].x =-450, P[1].y =-100;
	P[2].x =-350, P[2].y =-250;
	P[3].x =-250, P[3].y = 200;
	P[4].x =-150, P[4].y = 100;
	P[5].x =-50,  P[5].y = 150;
	P[6].x = 40, P[6].y = 10;
	P[7].x = 100, P[7].y = -60;
	P[8].x = 150, P[8].y = 80;
	P[9].x = 200, P[9].y = 70;
	P[10].x =230,P[10].y =-10;
	P[11].x =300,P[11].y =-200;
	P[12].x =400,P[12].y = 150;
	P[13].x =520,P[13].y = 250;
	n = 13;
}

2.4.2 绘制型值点

void CGeometricfiguretestView::DrawDataPoint(CDC* pDC)//绘制型值点
{
	CBrush NewBrush, *pOldBrush;
	NewBrush.CreateSolidBrush(RGB(0, 0, 0));
	pOldBrush = pDC->SelectObject(&NewBrush);
	for( int i = 1; i < 13; i++)
		pDC->Ellipse(ROUND(P[i].x - 5), ROUND(P[i].y - 5), ROUND(P[i].x + 5), ROUND(P[i].y + 5));
	pDC->SelectObject(pOldBrush);
	pDC->Ellipse(ROUND(P[0].x - 5), ROUND(P[0].y - 5), ROUND(P[0].x + 5), ROUND(P[0].y + 5));
	pDC->Ellipse(ROUND(P[13].x - 5), ROUND(P[13].y - 5), ROUND(P[13].x + 5), ROUND(P[13].y + 5));
}

2.4.3 计算与绘制

void CGeometricfiguretestView::DrawCardinalCurve(CDC* pDC)//Cardinal曲线
{
	double M[4][4];
	double u=0.2;
	double s=(1-u)/2;
	CP2 p;
	M[0][0]=-s ,M[0][1]=2-s,M[0][2]= s-2 ,M[0][3]= s;//Mc矩阵
	M[1][0]=2*s,M[1][1]=s-3,M[1][2]=3-2*s,M[1][3]=-s;
	M[2][0]=-s ,M[2][1]= 0 ,M[2][2]=  s  ,M[2][3]= 0;
	M[3][0]= 0 ,M[3][1]= 1 ,M[3][2]=  0  ,M[3][3]= 0;
	double t3,t2,t1,t0;
	CPen pen(PS_SOLID,2,RGB(0,0,0));
	CPen* pOldPen=pDC->SelectObject(&pen);
	pDC->MoveTo(ROUND(P[1].x),ROUND(P[1].y));
	for(int i=0; i< n-2; i++)
	{
		Point[0]=P[i],Point[1]=P[i+1],Point[2]=P[i+2],Point[3]=P[i+3];
		MultiplyMatrix(M, P, i);
		double tStep = 0.001;
		for(double t=0.0; t<1; t += tStep)
		{
			t3 = t*t*t; t2 = t*t; t1 = t; t0 = 1;
			p = t3*Point[0] + t2*Point[1] + t1*Point[2] + t0*Point[3];
			pDC->LineTo(ROUND(p.x),ROUND(p.y));
		}
	}
	pDC->SelectObject(pOldPen);
}

void CGeometricfiguretestView::MultiplyMatrix(double M0[][4], CP2 P0[4], int n)
{
	for(int i=0;i<4;i++)
		Point[i] = M0[i][0]*P0[n] + M0[i][1]*P0[n+1] + M0[i][2]*P0[n+2] + M0[i][3]*P0[n+3];
}

其中定义MultiplyMatrix函数为了实现4x4的Mc矩阵与1x4的边界约束矩阵的乘法计算。编译运行，如下：

我们也可以改变一下张力参数来试一下：

double u=1.0;

结果如下：

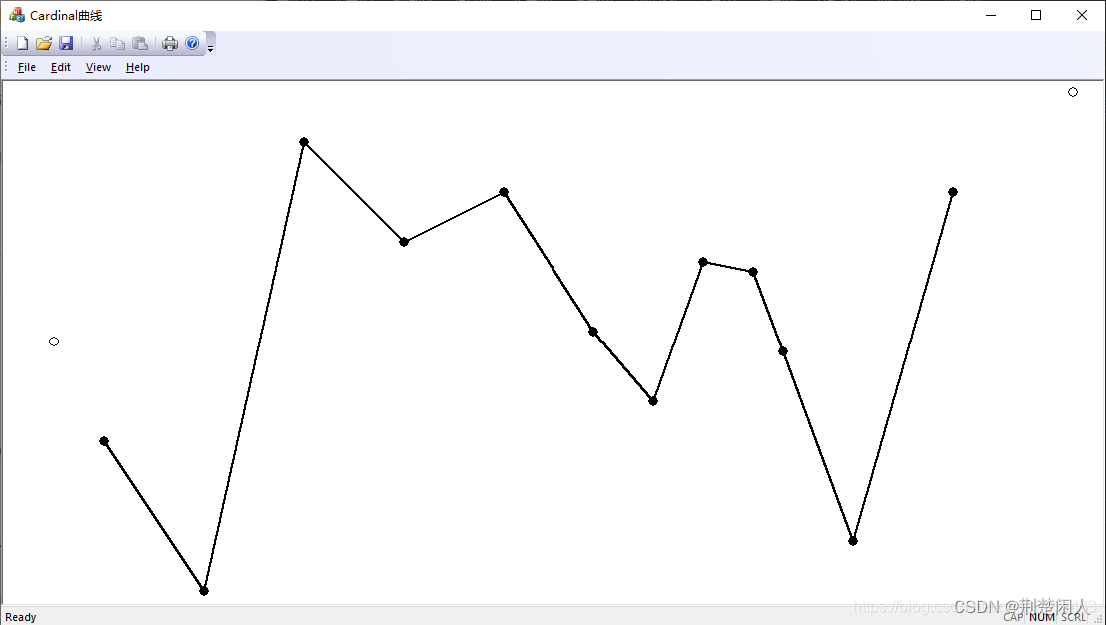
以上是MFC实现的代码，Qt的实现参见：Qt实现三次样条Cardinal曲线

如果想实现3D版的Cardinal曲线，请参考：osg实现三次样条Cardinal曲线

本文转自：计算几何03_三次参数样条曲线与Cardinal曲线

荆楚闲人

关注

3
点赞
踩
4

收藏

觉得还不错? 一键收藏
3
评论
三次参数样条曲线与Cardinal曲线

已知n个型值点Pi(xi, yi), i = 1, 2,…, n且相邻型值点不重合；型值点Pi在函数 p(t) 上。p(t) 在整个区间[P1, Pn]上二阶连续可导。在每个子区间[Pi, Pi+1], i = 1, 2,…, n-1上，分段函数 p(t) 都是参数t的三次多项式。则称函数是过型值点的三次参数样条函数，由三次参数样条函数构成的曲线称为三次参数样条曲线。其中，
复制链接

扫一扫