================================================================================
算算有相当一段时间没写blog了,主要是这学期作业比较多,而且我也没怎么学新的东西
接下来打算实现一个小的toy lib:DML,同时也回顾一下以前学到的东西
当然我只能保证代码的正确性,不能保证其效率啊~~~~~~
之后我会陆续添加进去很多代码,可以供大家学习的时候看,实际使用还是用其它的吧
================================================================================
一.引入
决策树基本上是每一本机器学习入门书籍必讲的东西,其决策过程和平时我们的思维很相似,所以非常好理解,同时有一堆信息论的东西在里面,也算是一个入门应用,决策树也有回归和分类,但一般来说我们主要讲的是分类,方便理解嘛。
虽然说这是一个很简单的算法,但其实现其实还是有些烦人,因为其feature既有离散的,也有连续的,实现的时候要稍加注意
(不同特征的决策,图片来自【1】)
O-信息论的一些point:
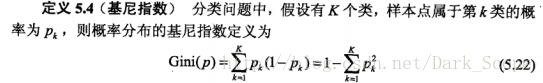


二.各种算法
1.ID3
ID3算法就是对各个feature信息计算信息增益,然后选择信息增益最大的feature作为决策点将数据分成两部分
然后再对这两部分分别生成决策树。

2.C4.5
C4.5与ID3相比其实就是用信息增益比代替信息增益,应为信息增益有一个缺点:
信息增益选择属性时偏向选择取值多的属性
算法的整体过程其实与ID3差异不大:图自【2】
3.CART
CART(classification and regression tree)的算法整体过程和上面的差异不大,然是CART的决策是二叉树的
每一个决策只能是“是”和“否”,换句话说,即使一个feature有多个可能取值,也只选择其中一个而把数据分类
两部分而不是多个,这里我们主要讲一下分类树,它用到的是基尼指数:

三.代码及实现
好吧,其实我就想贴贴代码而已……本代码在https://github.com/justdark/dml/tree/master/dml/DT
纯属toy~~~~~实现的CART算法:
from __future__ import division
import numpy as np
import scipy as sp
import pylab as py
def pGini(y):
ty=y.reshape(-1,).tolist()
label = set(ty)
sum=0
num_case=y.shape[0]
#print y
for i in label:
sum+=(np.count_nonzero(y==i)/num_case)**2
return 1-sum
class DTC:
def __init__(self,X,y,property=None):
'''
this is the class of Decision Tree
X is a M*N array where M stands for the training case number
N is the number of features
y is a M*1 vector
property is a binary vector of size N
property[i]==0 means the the i-th feature is discrete feature,otherwise it's continuous
in default,all feature is discrete
'''
'''
I meet some problem here,because the ndarry can only have one type
so If your X have some string parameter,all thing will translate to string
in this situation,you can't have continuous parameter
so remember:
if you have continous parameter,DON'T PUT any STRING IN X !!!!!!!!
'''
self.X=np.array(X)
self.y=np.array(y)
self.feature_dict={}
self.labels,self.y=np.unique(y,return_inverse=True)
self.DT=list()
if (property==None):
self.property=np.zeros((self.X.shape[1],1))
else:
self.property=property
for i in range(self.X.shape[1]):
self.feature_dict.setdefault(i)
self.feature_dict[i]=np.unique(X[:,i])
if (X.shape[0] != y.shape[0] ):
print "the shape of X and y is not right"
for i in range(self.X.shape[1]):
for j in self.feature_dict[i]:
pass#print self.Gini(X,y,i,j)
pass
def Gini(self,X,y,k,k_v):
if (self.property[k]==0):
#print X[X[:,k]==k_v],'dasasdasdasd'
#print X[:,k]!=k_v
c1 = (X[X[:,k]==k_v]).shape[0]
c2 = (X[X[:,k]!=k_v]).shape[0]
D = y.shape[0]
return c1*pGini(y[X[:,k]==k_v])/D+c2*pGini(y[X[:,k]!=k_v])/D
else:
c1 = (X[X[:,k]>=k_v]).shape[0]
c2 = (X[X[:,k]<k_v]).shape[0]
D = y.shape[0]
#print c1,c2,D
return c1*pGini(y[X[:,k]>=k_v])/D+c2*pGini(y[X[:,k]<k_v])/D
pass
def makeTree(self,X,y):
min=10000.0
m_i,m_j=0,0
if (np.unique(y).size<=1):
return (self.labels[y[0]])
for i in range(self.X.shape[1]):
for j in self.feature_dict[i]:
p=self.Gini(X,y,i,j)
if (p<min):
min=p
m_i,m_j=i,j
if (min==1):
return (y[0])
left=[]
righy=[]
if (self.property[m_i]==0):
left = self.makeTree(X[X[:,m_i]==m_j],y[X[:,m_i]==m_j])
right = self.makeTree(X[X[:,m_i]!=m_j],y[X[:,m_i]!=m_j])
else :
left = self.makeTree(X[X[:,m_i]>=m_j],y[X[:,m_i]>=m_j])
right = self.makeTree(X[X[:,m_i]<m_j],y[X[:,m_i]<m_j])
return [(m_i,m_j),left,right]
def train(self):
self.DT=self.makeTree(self.X,self.y)
print self.DT
def pred(self,X):
X=np.array(X)
result = np.zeros((X.shape[0],1))
for i in range(X.shape[0]):
tp=self.DT
while ( type(tp) is list):
a,b=tp[0]
if (self.property[a]==0):
if (X[i][a]==b):
tp=tp[1]
else:
tp=tp[2]
else:
if (X[i][a]>=b):
tp=tp[1]
else:
tp=tp[2]
result[i]=self.labels[tp]
return result
pass
这个maketree让我想起了线段树………………代码里的变量基本都有说明
试验代码:
from __future__ import division
import numpy as np
import scipy as sp
from dml.DT import DTC
X=np.array([
[0,0,0,0,8],
[0,0,0,1,3.5],
[0,1,0,1,3.5],
[0,1,1,0,3.5],
[0,0,0,0,3.5],
[1,0,0,0,3.5],
[1,0,0,1,3.5],
[1,1,1,1,2],
[1,0,1,2,3.5],
[1,0,1,2,3.5],
[2,0,1,2,3.5],
[2,0,1,1,3.5],
[2,1,0,1,3.5],
[2,1,0,2,3.5],
[2,0,0,0,10],
])
y=np.array([
[1],
[0],
[1],
[1],
[0],
[0],
[0],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
[1],
])
prop=np.zeros((5,1))
prop[4]=1
a=DTC(X,y,prop)
a.train()
print a.pred([[0,0,0,0,3.0],[2,1,0,1,2]])
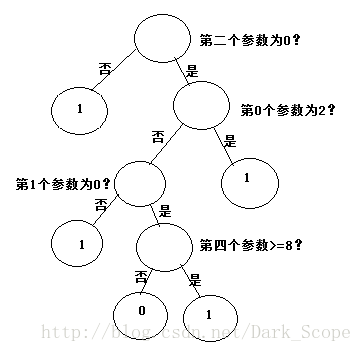
可以看到可以学习出一个决策树:
展示出来大概是这样:注意第四个参数是连续变量












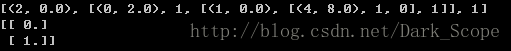














 7839
7839

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








