《机器学习实战》 CH3
决策树基本原理与实现。
决策树基本原理可以概括为:通过计算信息增益划分属性集,选择增益最大的属性作为决策树当前节点,依次往下,构建整个决策树。为了计算熵,需要先计算每个属性的信息增益值,通过下面公式计算:
创建数据集:
def createDataSet():
dataSet = [ [1, 1, 'yes'],
[1, 1, 'yes'],
[1, 0, 'no'],
[0, 1, 'no'],
[0, 1, 'no']]
labels = ['no surfacing','flippers']
return dataSet, labels计算熵代码片:
def calcShannonEnt(dataSet):
numEntries = len(dataSet) #计算数据集中实例总数
print 'total numEntries = %d' % numEntries
labelCounts = {} #创建数据字典,计算每个label出现的次数
for featVec in dataSet: #the the number of unique elements and their occurance
currentLabel = featVec[-1] # -1表示获取最后一个元素,即label
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
for key in labelCounts.keys():#打印字典
print key,':',labelCounts[key]
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key])/numEntries
shannonEnt -= prob * log(prob,2) #log base 2
print 'shannonEnt = ',shannonEnt
return shannonEntlabelCounts 是存储所有label个数的字典,key为label,key_value为label个数。for循环计算label个数,并打印出字典值。函数返回熵值。
myDat, labels = createDataSet()
shannonEnt = calcShannonEnt(myDat)
计算结果为:
numEntries = 5
yes : 2
no : 3
shannonEnt = 0.970950594455
熵值越高,数据集越混乱(label越多,越混乱)。试着改变label值可以观察熵值的变化。
myDat[0][-1] = ‘maybe’
shannonEnt = calcShannonEnt(myDat)
输出结果:
numEntries = 5
maybe : 1
yes : 1
no : 3
shannonEnt = 1.37095059445
得到熵值后即可计算各属性信息增益值,选取最大信息增益值作为当前分类节点,知道分类结束。
splitDataSet函数参数为:dataSet为输入数据集,包含你label值;axis为每行的第axis元素,对应属性特征;value为对应元素的值,即特征的值。
函








 本文介绍了决策树的基本原理,包括通过计算信息增益来划分属性集,并提供了Python实现的详细步骤。从创建数据集到计算熵,再到选择最佳特征进行分类,最后构建和分类决策树的过程清晰阐述。
本文介绍了决策树的基本原理,包括通过计算信息增益来划分属性集,并提供了Python实现的详细步骤。从创建数据集到计算熵,再到选择最佳特征进行分类,最后构建和分类决策树的过程清晰阐述。
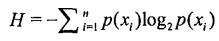
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 7万+
7万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








