算法导论第三版第3章习题答案

时时处处皆修行

于 2020-10-28 00:00:08 发布

阅读量8k

点赞数 3

分类专栏： Algorithm 文章标签：算法导论

本文链接：https://blog.csdn.net/davidwang9527/article/details/109322500

版权

Algorithm 专栏收录该内容

8 篇文章 14 订阅

订阅专栏

2020/10/28:初稿，参考https://ita.skanev.com/，修订参考文献的部分错误

2020/10/30:修订第二节第4题的证明错误(参考https://blog.csdn.net/qq_36414798/article/details/81028403)

3 Growth of Functions

3.1 Asymptotic notation

1.Let f(n) + g(n) be asymptotically nonnegative functions. Using the basic definition of Θ-notation, prove that max(f(n),g(n))=Θ(f(n)+g(n)).

From asymptotically nonnegative, we can assume that:

$\begin{align*} \exists n_1, n_2: & f(n) \geq 0 & \text{for } n > n_1 \\ & g(n) \geq 0 & \text{for } n > n_2 \end{align*}$

Let , some obvious things for n > n_0 :

$f(n) \leq \max(f(n), g(n)) \\ g(n) \leq \max(f(n), g(n)) \\ \big(f(n) + g(n)\big)/2 \leq \max(f(n), g(n)) \\ \max(f(n), g(n)) \leq f(n) + g(n)$

From the last two inequalities, we get:

$0 \leq \frac{1}{2}\big(f(n) + g(n)\big) \leq \max\big(f(n), g(n)\big) \leq f(n) + g(n) \quad \text{for } n > n_0$

Which is the definition of $\Theta(f(n) + g(n))$ with c_1 = 1/2, c_2 = 1

2.Show that for any real constants a and b, where b>0, $(n + a)^b = \Theta(n^b)$

$(n + a)^b = \binom{n}0n^b + \binom{n}1n^{b-1}b + \cdots + \binom{n}0a^b$

The most significant term is n^b and this is obviously polynomially tightly bound.

3.Explain why the statement, "The running time of algorithm A is at least is meaningless.

The O-notation provides an upper bound. "At least" implies a lower bound.

4.Is $2^{n+1} = O(2^n)$ ? Is $2^{2n} = O(2^n) ?$

Yes, because if we choose 2 for both constants in the O-notation definition, we get an equality.

No, because $\nexists c: 2^n \cdot 2^n \leq c 2^n$

5.Prove Theorem 3.1

The theorem states:

For any two functions f(n) and g(n), we have f(n)=Θ(g(n)) if and only if f(n)=O(g(n)) and f(n)=Ω(g(n))

6.Prove that the running time of an algorithm is Θ(g(n)) if and only if its worst-case running time is O(g(n)) and its best-case running time is Ω(g(n)).

7.Prove o(g(n))∩ω(g(n)) is the empty set.

8.We can extend our notation to the case of two parameters n and m that can go to infinity independently at different rates. For a given function g(n,m) we denote O(g(n,m)) the set of functions:

$\begin{align*} O(g(n, m) = \lbrace f(n, m): &\text{there exist positive constants } c, n_0, \text{ and } m_0 \\ &\text{such that } 0 \leq f(n, m) \leq cg(n, m) \\ &\text{for all } n \geq n_0 \text{ or } m \geq m_0. \end{align*}$

Give corresponding definitions for Ω(g(n,m)) and Θ(g(n,m)).

3.2 Standard notations and common functions

1.Show that if f(n) and g(n) are monotonically increasing functions, then so are the functions f(n)+g(n) and f(g(n)), and if f(n) and g(n) are in addition nonnegative, then f(n)⋅g(n) is monotonically increasing.

2.Prove equation (3.16)

$\begin{align*} a^{\log_bc} = a^{\frac{\log_ac}{\log_ab}} = \big(a^{\log_ac})^\frac{1}{\log_ab} = c^{\log_ba} \end{align*}$

3.Prove equation (3.19). Also prove that n!=ω() and n!=o().

4.Is the function ⌈lgn⌉! polynomially bounded? Is the function ⌈lglgn⌉! polynomially bounded?

⌈lgn⌉! is not polynomially bounded, but ⌈lglgn!⌉ is.

If we take the definition of polynomially bound:
$f(n) \leq cn^k$

and take the logarithm of each side, we get:

$\lg{f(n)} \leq \lg{c} + k\lg{n}$

Thus, a function is polynomially bound if $\lg{f(n)} = \O(\lg{n})$

In the following proofs, we will make use of the following two facts:

lg(n!) = Θ(nlgn) (by equation (3.19))

⌈lgn⌉ = Θ(lgn), because

· ⌈lgn⌉ ≥ lgn

· ⌈lgn⌉ ≤ lgn + 1 ≤ 2lgn, for all n ≥ 2

lg(⌈lgn⌉!) = Θ(⌈lgn⌉lg⌈lgn⌉) = Θ(lgn lg lgn) = ω(lgn).Therefore, lg(⌈lgn⌉!) ≠ Ο(lgn), and so ⌈lgn⌉! is not polynomially bounded.

lg(⌈lglgn⌉!) = Θ(⌈lglgn⌉lg⌈lglgn⌉) = Θ(lglgn lg lglgn) = $o((\lg{\lg{n}})^2)$ = $o(\lg^2\lg(n))$ = ο(lgn) .

The last step above follows from the property that any polylogarithmic function grows more slowly than any positive polynomial function, i.e., that for constants a, b ＞ 0, we have $\lg^b{n}$ = o(n^a) . Substitute lgn for n, 2 for b, and 1 for a, giving $\lg^2{(\lg{n})}=o(lgn)$ .

Therefore, lg(⌈lglgn⌉!) = Ο(lgn), and so ⌈lglgn⌉! is polynomially bounded.

5. Which is asymptotically larger: $\lg(\lg\textup{*}{n})or\lg\textup{*}(\lg{n})$

The second, because:

$\lg\textup{*}(\lg{n}) = \lg^*n - 1 > \lg(\lg\textup{*}(n))$

6.Show that the golden ratio ϕ and its conjugate $\hat \phi$ both satisfy the equation .

7.Proove by induction that the ith Fibonacci number satisfies the equality

$F_i = \frac{\phi^i - \hat{\phi^i}}{\sqrt5}$

Base:

$\frac{\phi^0 - \hat{\phi^0}}{\sqrt{5}} = \frac{1 - 1}{\sqrt{5}} = 0 = F_0$

$\frac{\phi - \hat{\phi}}{\sqrt{5}} = \frac{1 + \sqrt{5} - 1 + \sqrt{5}}{2\sqrt{5}} = 1 = F_1$

Step:

$F_{n + 2} = F_{n + 1} + F_n = \frac{\phi^{n+1} - \hat\phi^{n+1}}{\sqrt{5}} + \frac{\phi^n - \hat{\phi^n}}{\sqrt{5}} = \frac{\phi^n(\phi + 1) - \hat{\phi^n}(\hat\phi + 1)}{\sqrt{5}} = \frac{\phi^n\phi^2 - \hat{\phi^n}\hat{\phi^2}}{\sqrt{5}} = \frac{\phi^{n+2} + \hat\phi^{n+2}}{\sqrt{5}}$

8.Show that $k\ln{k} = \Theta(n)$ implies $k = \Theta(n/\ln{n})$ .

Problem

3.1 Asymptotic behavior of polynomials

3.2 Asymptotic behavior of polynomials

Indicate for each pair of expressions (A,B) in the table below, whether A is O, o, Ω, ω, or Θ of B. Assume that k≥1, ϵ>0, and c>1 are constants. Your answer should be in the form of the table with "yes" or "no" written in each box.

Note: $lg(n!)=\Theta(nlgn)$

3.3 Ordering by asymptotic growth rates.

a.Rank the following functions by order of growth;that is, find an arrangement $g_1, g_2, \ldots , g_{30}$ of the functions $g_1 = \Omega(g_2), g_2 = \Omega(g_3), \ldots, g_{29} = \Omega(g_{30})$ . Partition your list into equivalence classes such that functions f(n) and g(n) are in the same class if and only if $f(n) = \Theta(g(n))$ .

b.Give an example of a single nonnegative function f(n) such that for all functions gi(n) in part (1), f(n) is neither nor $\Omega(g_i(n))$ .

The order is thus:

$1 = n^{1/\lg{n}}$
$\lg(\lg^*n)$
$\lg\textup{*}n \simeq \lg\textup{*}(\lg{n})$

The asked function can be: $2^{2^{(n + 1)\sin{x}}}$

3.4 Asymptotic notation properties

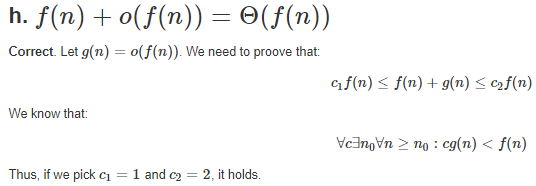
3.5 Variations on O and Ω

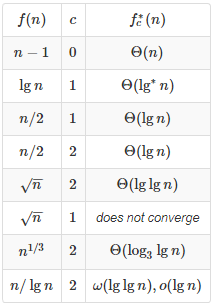
3.6 Iterated functions

时时处处皆修行

关注

3
点赞
踩
61

收藏

觉得还不错? 一键收藏
0
评论
算法导论第三版第3章习题答案

2020/10/28:初稿，参考https://ita.skanev.com/，修订参考文献的部分错误2020/10/30:修订第二节第4题的证明错误(参考https://blog.csdn.net/qq_36414798/article/details/81028403)
复制链接

扫一扫