循环数组实现单调队列和解决滑动窗口

1.循环数组实现单调队列

1.1 普通队列实现

• 普通的队列数据结构:先进先出，这里的“进”就是数据从队列的尾进，这里的“出”就是从队列的头出。
• 很显然循环数组队列比单方向的数组队列的效率更高，更优，这里我就不再过多赘述。

1.1.1定义循环队列（循环队列的结构）

（1）首先是如何确定队列的“首尾”，这里我用两个变量head，tail，它们分别存储着循环队列首尾元素的数组下标。
（2）如何实现循环？：注意因为队列的元素一定是在 head–tail之间的，而很显然，这可以有两种情况吧，一种是顺势针，一种是逆时针，如下图，为了方便我们选择顺时针这种情况

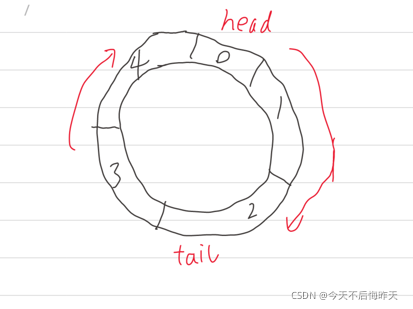
（3）如何利用head和tail的位置关系推断出队列空还是满如上图所示，数组有5个空间，那么队列数据的存放就有6种情况，，分别是0个，1个。。。。5个，那么head和tail的相对情况则只有5种，分别是 0（tail=head），1（tail与head相邻），2（相隔一个空间）。。4（相隔三个空间）。那么这里我们用5种情况去表示6种状态，很显然一定会有1种情况表示了两种状态，很显然不行

• 对此解决方法是我们留一个空间不用，这样队列数据的存放情况就少了一种（比如上图我们最多能放4个数据，就只有5种情况）。
• （4）这里我进行了一些小改变，为了方便，**head变量存储着队首元素的坐标，而tail变量这里存储为空，但是它“”前面的“”一个位置，存储着队列的尾元素坐标，如下图

1.1.2循环队列的操作（outqueue、inqueue）

用此图为例

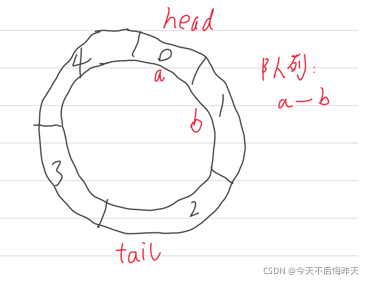
(1)出队：head顺时针移动对应”head=head+1“
注意当head=4时候 head=head+1，此时head=5，数组溢出
所以我们改一下 head=（head+1）%length（array），这里就是head=（head+1）%4；

int out_queue_head(int*queue,int*headp,int length) {
	int temp = queue[*headp];
	*headp = (*headp + 1) % length;
	return temp;
}

(2)入队：tail顺时针移动一位,同上

bool inqueue_fromtail(int*queue, int* tailp, int value,int length) {
	queue[*tailp] = value;
	*tailp=(*tailp + 1) % length;
	return true;
}

（3）队空:if(tail==head)

bool isempty(int* queue, int* headp, int* tailp) {
	if (*headp == *tailp) {
		return true;
	}
	return false;
}

（4）队满:if(tail==（tail+1）%length（array）)

bool isfull(int* queue, int* headp, int* tailp,int length) {
	if ((*tailp + 1) % length == *headp) {
		return true;
	}
	return false;
}

1.2单调队列实现

1.2.1单调队列定义

• 单调队列：一个队列的数据总是满足单调递增或者递减（根据问题需求决定），而且只能队首或队尾出队，只能队尾进队，不能队首进队
• 详情请看其他博主单调队列的详情解答

1.2.2单调队列操作

首先我们之前实现了队首出队和队尾进队操作，下面就剩队尾出队操作
(1)队尾出队
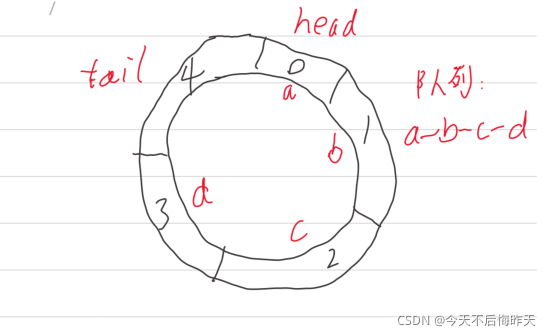
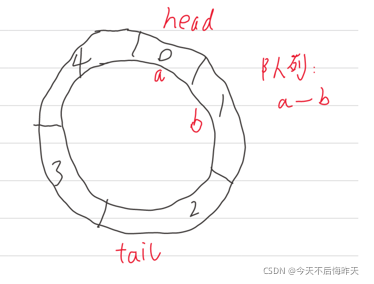
以此图为例，队尾出队很显然是tail向逆时针走一个单位，即“tail=tail-1”
那么一旦遇到数组坐标的减法，一定需要保证在数组范围之内当tail=0，tail-1=-1，显然出现错误

int out_queue_tail(int* queue, int* tailp,int length) {
	if (*tailp == 0) {
		int temp = queue[length - 1];
		*tailp = length-1;
		return temp;
	}//对于特殊情况进行处理
	else {
		int temp = queue[*tailp - 1];
		*tailp = (*tailp - 1) % length;
		return temp;
	}
}

1.3解决滑动窗口问题

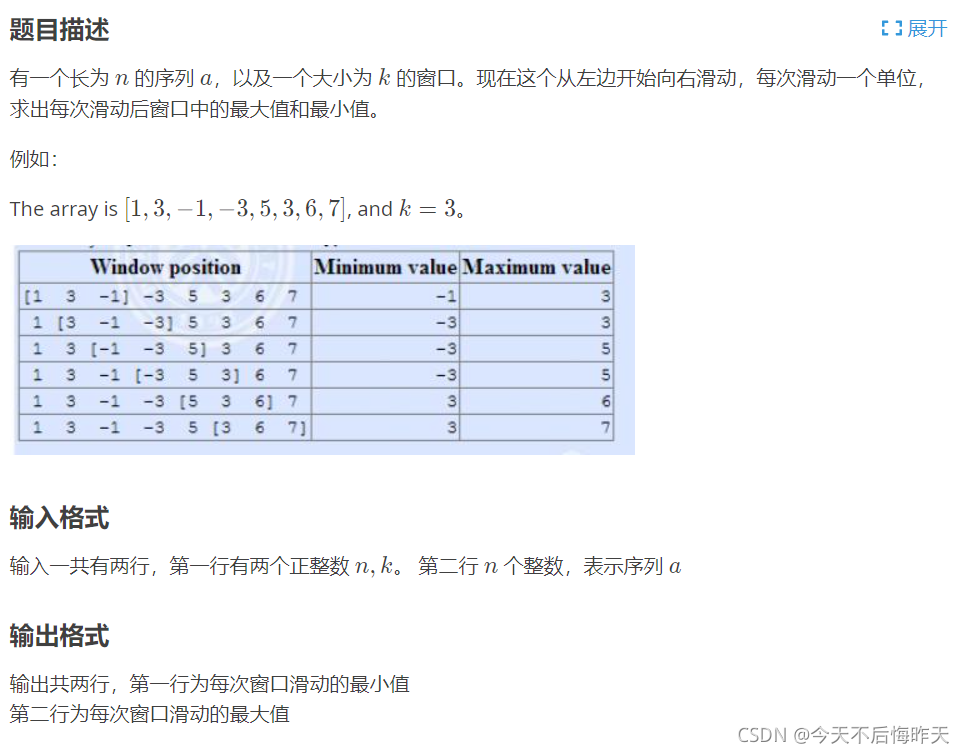
（1）通常想法如何将单调队列运用到题目中？很显然单调队列的队首一定是队列中最大或者最小的元素，根据题目要求就是要求区间内的最大最小值，如果我们能把这个区间内的所有元素，依次放入一个单调队列，那么最后把队首元素打印就得到结果
（2）如何读进去单调队列（递减），我简单说一下，要保证单调队列递减的性质，当我们从data数组读出一个数据data_i的时候，我们需要拿data_i和队列的尾元素（队列中最大的）进行比较，如果data_i大于它，则把队列的尾元素out，继续比较下一个队列尾元素，直到队列为空或者队列尾元素小于data_i，我们再把data_i入队即可。入完队后就print 队首元素（最小的）
（3）需要注意的是：
①如果该数不在区间范围内，则需要踢掉，
②需要依次读入每个数据，但是打印的时候需要注意：①当data数组长度>=区间长度（k）时候，我们是将第k个元素放到单调队列中进去后，再print单调队列的首元素，而我们在前1到k-1个元素都没有print，而是一直读。
②当当data数组长度<区间长度的时候，我们的代码就有变化，需要读完之后就直接print单调队列的首元素，但是读入单调队列的代码没有变化，前提需要一个判断
③为了方便判断队首是否在区间范围内，队列中只是存储着data数组中元素的下标值
④为啥只用判断队首是否在区间内，而不是其他元素呢？：自己模拟一下过程

全部代码（输出最小值）

如果要输出最大值，就把单调队列的比较符号改变就行了

#include<stdio.h>
#include<malloc.h>
int max(int n, int m) {
	return n - m > 0 ? n : m;
}
int min(int n, int m) {
	return n - m > 0 ? m : n;
}
int out_queue_head(int*queue,int*headp,int length) {
	
	int temp = queue[*headp];
	*headp = (*headp + 1) % length;
	return temp;
}
int out_queue_tail(int* queue, int* tailp,int length) {
	if (*tailp == 0) {
		int temp = queue[length - 1];
		*tailp = length-1;
		return temp;
	}//对于特殊情况进行处理
	else {
		int temp = queue[*tailp - 1];
		*tailp = (*tailp - 1) % length;
		return temp;
	}
}
bool inqueue_fromtail(int*queue, int* tailp, int value,int length) {
	queue[*tailp] = value;
	*tailp=(*tailp + 1) % length;
	return true;
}
bool isempty(int* queue, int* headp, int* tailp) {
	if (*headp == *tailp) {
		return true;
	}
	return false;
}
bool isfull(int* queue, int* headp, int* tailp,int length) {
	if ((*tailp + 1) % length == *headp) {
		return true;
	}
	return false;
}
int get_head_queue(int* queue, int* headp) {
	return queue[*headp];
}
int get_tail_queue(int* queue, int* tailp,int length) {
	if (*tailp == 0) {
		int temp = queue[length - 1];
		return temp;
	}
	else return queue[((*tailp)-1) % length];
}
int  main() {
	int head = 0, tail = 0, i_max = 0, i_min = 0;
	bool flag_min = true;
	int dataSize, k;
	scanf("%d %d", &dataSize, &k);
	int lengthqueue = k + 1;
	int* data = (int*)malloc(sizeof(int) * dataSize);
	for (int i = 0; i < dataSize; i++)
		scanf("%d", &data[i]);
	int* queue = (int*)malloc(sizeof(int) * (k + 1));//用循环数组实现队列
	// 队列中储存的是数据的数组下标!!!!!!
	if (k > dataSize) {
		for (int i = 0; i < dataSize && i < k - 1; i++) {
			while (1) {
				if (!isempty(queue, &head, &tail) && data[i] <= data[get_tail_queue(queue, &tail, lengthqueue)]) {
					out_queue_tail(queue, &tail, lengthqueue);
					continue;//while
				}

				else {
					if (!isfull(queue, &head, &tail, lengthqueue)) {
						inqueue_fromtail(queue, &tail, i, lengthqueue);//入队
						break;//while
					}
				}
			}
			if (i == dataSize - 1) {
				printf("%d ", data[get_head_queue(queue, &head)]);
			}
		}
		return 0;
	}// end_if当数组长度<区间长度的操作

	for (int i = 0; i < dataSize; i++) {
		if (!isempty(queue, &head, &tail)) {
			if (i - get_head_queue(queue, &head) >= k)
				out_queue_head(queue, &head, lengthqueue);
		}
		//判断队列的第一个数是否超过了k范围
		while (1) {
			if (!isempty(queue, &head, &tail) && data[i] <= data[get_tail_queue(queue, &tail, lengthqueue)]) {
				out_queue_tail(queue, &tail, lengthqueue);
				continue;//while
			}

			else {
				if (!isfull(queue, &head, &tail, lengthqueue)) {
					inqueue_fromtail(queue, &tail, i, lengthqueue);//入队
					break;//while
				}
			}
		}
		if (i >= k - 1) {
			printf("%d ", data[get_head_queue(queue, &head)]);
		}
	}//当数组长度>=区间长度的操作
	printf("\n");
	head = 0, tail = 0;
	return 0;
}