计算几何——n条线段求交Bentley-Ottmann算法可视化实现

最新推荐文章于 2023-10-17 08:46:51 发布

别看着我笑了

最新推荐文章于 2023-10-17 08:46:51 发布

阅读量5.4k

点赞数 1

CC 4.0 BY-SA版权

分类专栏：计算几何

本文链接：https://blog.csdn.net/derbi123123/article/details/106531120

对于平面上的N条线段求交点，若使用最直接的方法，即两两求其交点，则(N-1) + (N-2)+…1 = N(N-1)/2次运算，时间复杂度是O(n²)。这种方法对交点个数接近N(N-1)/2的情况可行，但大多数情况下，N条线段形成的交点个数是较少的，此时算法可调整成与输入线段个数和输出的交点个数相关的效率更高的方法，如Bentley-Ottmann 算法。

求N条线段的所有交点——Bentley-Ottmann算法

1.算法的思路

以X轴升序对所有左右端点构造事件队列priority queue（优先队列）和初始化扫描线BBST（对于扫描线相交的线段按y值升序排列）后,对顶点队列中所有元素开始循环（不断从事件队列中取出top元素）。

当取出的元素为线段的左端点时

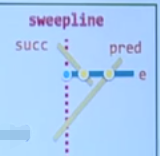
在这里插入图片描述
首先将此条线段插入到扫描线BBST中，同时以Y轴的升序重排链表中所有元素，然后分别计算此条线段与其在扫描线段BBST中上下相邻线段（前驱和后继线段）的相交情况，若有交点，则将交点插入到顶点队列中。

当取出的元素为线段的右端点时

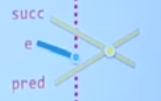
在这里插入图片描述
首先将此条线段从扫描线BBST中删除，然后计算此时与此条线段上下相邻的那两条线段（前驱和后继线段）之间的相交情况，如果有交点，但在顶点队列中还不存在，则将其插入顶点队列。

当取出的元素为交点时

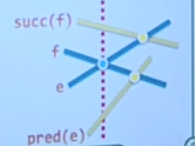
在这里插入图片描述
首先将这个交点增加到最后要输出的结果集合中。然后得到这个交点从属的两条线段，交换它们在扫描线BBST中的位置后，分别与新紧邻的线段求交点，如果有交点，并在顶点队列中还不存在，则将其插入顶点队列。

以上3种情况分别处理后，从顶点队列中移走这个取出的元素。

LAST

当循环处理完毕（事件队列中无元素），结果集合中的元素即为所有的交点。

这种方法最后以一次循环取代了最直接的两两线段求交点的两次循环。不过，需要注意的是，当交点个数接近n²级别时，Bentley-Ottmann算法的效率比直接两两求其交点的方法低下。

2.算法的分析：

真正在影响效率的无非是事件队列的长度和与扫描线相交的线段数，对于n个segments(线段)，i个intersection（交点），显然事件队列最长也是2n+i，与扫描线相交的线段数最坏情况下是n，而对扫描线（BBST（平衡二叉搜索树）存储）的操作不过O(logn).
故Bentley-Ottmann代价：O((2n+i)*logn)——>O(nlogn)。

3.可视化实现

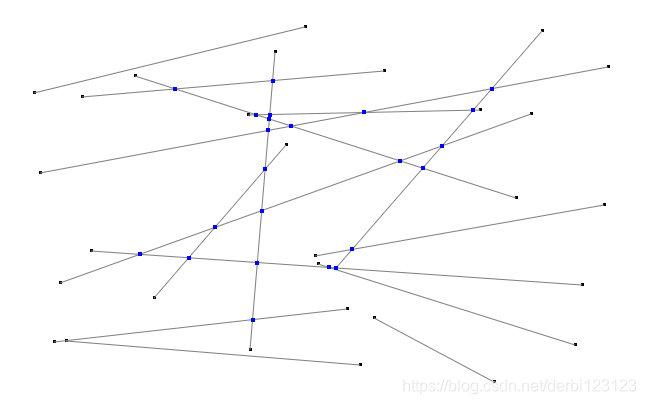
在这里插入图片描述
John Hany在GitHub上用OpenGL的实现方法：

tree类

/*
 *	Author: John Hany
 *	Website: http://johnhany.net/
 *	Source code updates: https://github.com/johnhany/SegmentsIntersection
 *	If you have any advice, you could contact me at: johnhany@163.com
 *
 */

#ifndef __SCAN_TREE_H
#define __SCAN_TREE_H

#include "POrder.h"

struct tree
{
   
   
	tree *left;
	tree *right;
	tree *father;
	POrder *id;
};

#define SCAN_UP 3
#define SCAN_L 4
#define SCAN_L2 5
#define SCAN_L_L2 11

#define LEN_S sizeof(struct tree)

void addIntoScan(struct tree *top,struct tree *now,float y_scan);
tree *searchInScan(tree *temp,int line,int line2,int srchType);
struct tree *dltFromScan(tree *top,tree *now);
struct tree *get_left(tree *now);
struct tree *get_right(tree *now);
void switchScan(tree* left_s,tree* right_s);

#endif

/*
 *	Author: John Hany
 *	Website: http://johnhany.net/
 *	Source code updates: https://github.com/johnhany/SegmentsIntersection
 *	If you have any advice, you could contact me at: johnhany@163.com
 *
 */

#include "windows.h"
#include "scanTree.h"

//Add a new node "now" into the scan tree "top".
//The position "now" to be placed is determined by the X axis
//on the sweep line(whose Y axis is y_scan).
void addIntoScan(struct tree *top,struct tree *now,float y_scan)
{
   
   
	struct tree *temp;
	temp=(struct tree *)malloc(LEN_S);
	temp=top;
	float x_now,x_temp;

	//Calculate the proper X axises.
	if(now->id->type==ORD_UPPER && (now->id->k!=-1 || now->id->b>0)){
   
   
		x_now=now->id->k * y_scan + now->id->b;
	}else{
   
   
		x_now=now->id->x;
	}
	if(temp->id->type==ORD_UPPER && (temp->id->k!=-1 || temp->id->b>0)){
   
   
		x_temp=temp->id->k * y_scan + temp->id->b;
	}else{
   
   
		x_temp=temp->id->x;
	}

	while((x_now < x_temp && temp->left!=NULL) || (x_now >= x_temp && temp->right!=NULL))
	{
   
   
		if(x_now < x_temp)
		{
   
   
			temp=temp->left;
		}else{
   
   
			temp=temp->right;
		}

		if(temp->id->type==ORD_UPPER && (temp->id->k!=-1 || temp->id->b>0)){
   
   
			x_temp=temp->id->k * y_scan + temp->id->b;
		}else{
   
   
			x_temp=temp->id->x;
		}
	}
	if(x_now < x_temp)
	{
   
   
		temp->left=now;
		now->father=temp;
	}else{
   
   
		temp->right=now;
		now->father=temp;
	}
	now->left=NULL;
	now->right=NULL;
}

//Search for node according to line numbers and type of the point.
//srchType==SCAN_L: search for upper point that it->l==line
//srchType==SCAN_L2: search for upper point that it->l==line2
//srchType==SCAN_L_L2: search for inte-point that it->l==line and it->l2==line2
tree *searchInScan(tree *temp,int line,int line2,int srchType)
{
   
   
	tree *out;
	out=(tree *)malloc(LEN_S);

	if(temp==NULL)
		return NULL;
	if(srchType==SCAN_L && temp->id->type==ORD_UPPER && temp->id->l==line)
		return temp;
	else if(srchType==SCAN_L2 && temp->id->type==ORD_UPPER && temp->id->l==line2)
		return temp;
	else if(srchType==SCAN_L_L2 && (temp->id->l==line && temp->id->l2==line2 || temp->id->l==line2 && temp->id->l2==line))
		return temp;
	else{
   
   
		//If the node doesn't meet any requirement,
		out=NULL;
		if(temp->left!=NULL)
		{
   
   
			//search further in its left sub-tree,
			out=searchInScan(temp->left,line,line2,srchType);
			if(out!=NULL)
				return out;
		}
		if(temp->right!=NULL)
		{
   
   
			//and its right sub-tree.
			out=searchInScan(temp->right,line,line2,srchType);
			if(out!=NULL)
				return out;
		}
		//If can't find any in its sub-trees.
		return NULL;
	}
}

//Delete a node "now" from the scan tree "top".
//If the root node changes because of the delete,
//the function returns the new root node.
//WARNING: NO FREE() FUNCTION
struct tree *dltFromScan(tree *top,tree *now)
{
   
   
	tree *temp;
	tree *new_top;
	temp=(tree *)malloc(LEN_S);

	if(now->father==NULL)
	{
   
   
		//To delete the root node.
		if(now->right!=NULL)
		{
   
   
			//If its right sub-tree exists.
			temp=now->right;
			new_top=temp;
			if(now->left!=NULL)
			{
   
   
				//If both of its left and right sub-tree exist.
				//Its left sub-tree becomes the left-most sub-tree
				//of its right sub-tree.
				while(temp->left!=NULL)
				{
   
   
					temp=temp->left;
				}
				temp->left=now->left;
				now->left->father=temp;
			}
			//Its right-tree knot becomes the new root node.
			now->right->father=NULL;
		}else if(now->left!=NULL)
		{
   
   
			//If its right sub-tree does not exist,
			//Its left sub-tree becomes the new root node.
			now->left->father=NULL;
			new_top=now->left;
		}else{
   
   
			//Both of its left and right sub-tree do not exist,
			//which means the scan tree is only root node itself.
			new_top=NULL;
		}
	}else{
   
   
		if(now->left==NULL)
		{
   
   
			if(now->right==NULL)
			{
   
   
				//If delete a leaf, only delete itself.
				//But we don't know which side sub-tree it is of its father.
				if(now->father->left!=NULL && now->father->left==now)
					now->father->left=NULL;
				else if(now->father->right!=NULL && now->father->right==now)
					now->father->right=NULL;
			}else{
   
   
				//If it does not have a left sub-tree, its right
				//sub-tree becomes the sub-tree of its father.
				now->right->father=now->father;
				if(now->father->left!=NULL && now->father->left==now)
					now->father->left=now->right;
				else if(now->father->right!=NULL && now->father->right==now)
					now->father->right=now->right;
			}
		}else{
   
   
			//If the node has both left and right sub-trees.
			//Its left sub-tree takes place of itself, and its right
			//sub-tree becomes the right-most sub-tree of its left sub-tree.
			now->left->father=now->father;
			if(now->father->left!=NULL && now->father->left==now)
				now->father->left=now->left;
			else if(now->father->right!=NULL && now->father->right==now)
				now->father->right=now->left;
			temp=now->left;
			if(now->right!=NULL)
			{
   
   
				while(temp->right!=NULL)
				{
   
   
					temp=temp->right;
				}
				now->right->father=temp;
				temp->right=now->right;
			}
		}
		new_top=top;