线性代数——第一章行列式

羽t

已于 2024-07-18 18:07:55 修改

阅读量966

点赞数 27

分类专栏：线性代数文章标签：线性代数

于 2024-06-29 17:37:21 首次发布

本文链接：https://blog.csdn.net/dfggc/article/details/140050951

版权

线性代数专栏收录该内容

1 篇文章 0 订阅

订阅专栏

1. 二阶与三阶行列式

1.1 二阶行列式

1.1.1 定义：

由二行二列四元素所成的算式，记作 $\begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix}=(+a_{11} *a_{22} )+(-a_{12} *a_{21} )=a_{11} *a_{22} -a_{12} *a_{21}$ ;

例如： $\begin{vmatrix} 3 & 2 \\ 8 & 7 \end{vmatrix}=3*7-2*8=5$ ； $\begin{vmatrix} -3 & 2 \\ 8 & 7 \end{vmatrix}=-3*7-2*8=-37$ .

1.1.2 注意：

1. 两项相加

2. 主为正号，副为负号

3. $a_{ij}$ : 一般， $i$ 为行标， $j$ 为列标，为第 $(i,j)$ 元

4. 不同行不同列相乘

5. 习惯：先写上行，再写下行

此类亦可：

$\begin{vmatrix} b_{1} & a_{12} \\ b_{2} & a_{22} \end{vmatrix}=b_{1}*a_{22}-a_{12}*b_{2}$

1.1.3 二阶行列式的意义

1.1.3.1 代数意义（求二元线性方程组）

$a_{11}x_{1}+a_{12}x_{2}=b_{1}\\a_{21}x_{1}+a_{22}x_{2}=b_{2}$ , 消 $x_{2}$ ,则可得

$(a_{11}a_{22}-a_{12}a_{21})x_{1}=b_{1}a_{22}-a_{12}b_{2}$ 若 $a_{11}a_{22}-a_{12}a_{21}\neq 0$ ,

则 $x_{1}=\frac{b_{1}a_{22}-a_{12}b_{2}}{a_{11}a_{22}-a_{12}a_{21}}=\frac{\begin{vmatrix} b_{1} & a_{12} \\ b_{2} & a_{22} \end{vmatrix}}{\begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix}}$

同理，消 $x_{1}$ 得 $x_{2}=\frac{\begin{vmatrix} a_{11} & b_{1} \\ a_{21} & b_{2} \end{vmatrix}}{\begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix}}$ , 规定 $\begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix}=D$ : 为系数行列式

且 $\begin{vmatrix} b_{1} & a_{12} \\ b_{2} & a_{22} \end{vmatrix}=D_{1}$ ， $\begin{vmatrix} a_{11} & b_{1} \\ a_{21} & b_{2} \end{vmatrix}=D_{2}$ ，则 $x_{1}=\frac{D_{1}}{D},x_{2}=\frac{D_{2}}{D}$ , 此为克莱姆法则

例1： $3x_{1}-2x_{2}=12 \\2x_{1}+x_{2}=1$ 其有且仅有一个解

注意：重点观查 $D$ 是否为 $0$ （行列成比例时，即 $\begin{vmatrix} a_{11} & a_{12} \\ ka_{21} & ka_{22} \end{vmatrix}=0$ ;

例2： $2x_{1}+x_{2}=3 \\4x_{1}+2x_{2}=5$ ，知 $D=\begin{vmatrix} 2 & 1 \\ 4 & 2 \end{vmatrix}=0$ ，可易知无解；（两直线平行）

例3： $2x_{1}+x_{2}=3 \\4x_{1}+2x_{2}=6$ ，可得有无数解。（两直线重合）

1.1.3.2 几何意义（二维空间中平行四边形面积）

$\begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix}=a_{11} *a_{22} -a_{12} *a_{21}$ ，

令 $\vec{m}=(a_{11},a_{12}),\left | \vec{m} \right |=m\\ \vec{n}= (a_{21},a_{22}),\left | \vec{n} \right |=n$ , 则在直角坐标系中，有

则 $S=m*h\\=m*n*\sin (\beta -\alpha )\\=m*n*(\sin\beta \cos\alpha - \cos\beta \sin\alpha )\\=m*\cos\alpha *n\sin\beta -m*\sin\alpha *n\cos \beta \\=a_{11}a_{22}-a_{12}a_{21}\\=\begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix}$

若 $\begin{vmatrix} a_{11} & a_{12} \\ ka_{21} & ka_{22} \end{vmatrix}=0$ ，则如图

1.2 三阶行列式

1.2.1 定义

三行三列9个元素构成的算式，记作： $\begin{vmatrix} a_{11} & a_{12}&a_{13}\\ a_{21} & a_{22} &a_{23}\\a_{31}&a_{32}&a_{33} \end{vmatrix}$ .

计算方法如图：

其等于:

$a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}+(-a_{13}a_{22}a_{31})+(-a_{12}a_{21}a_{33})+(-a_{11}a_{23}a_{32})$

例1： $\begin{vmatrix} 5 & 2&1 \\ 1 & 2&5\\34&1&34 \end{vmatrix}$

可以计算得： $340+340+1+(-68)+(-68)+(-25)=520$

（挺有趣的一个东西）

例2：

①： $\begin{vmatrix} a_{11} & a_{12}&a_{13}\\ 0 & a_{22} &a_{23}\\0&0&a_{33} \end{vmatrix}=a_{11}a_{22}a_{33}$

②： $\begin{vmatrix} a_{11} & 0&0\\ a_{21} & a_{22} &0\\a_{31}&a_{32}&a_{33} \end{vmatrix}=a_{11}a_{22}a_{33}$

③： $\begin{vmatrix} a_{11} & 0&0\\ 0 & a_{22} &0\\0&0&a_{33} \end{vmatrix}=a_{11}a_{22}a_{33}$

1.2.2 注意

1. 对角线法则，主为正号，副为负号

2. 6项相加

3. 先写上行（正），再写下行（负）

4. 不同行不同列相乘

5. 计算方法于此处特定适用（对角线法则仅适用于二阶与三阶，高阶有其它的方法）

1.2.3 三阶行列式的意义

1.2.3.1 代数意义（解三元线性方程组）

$x_{1}-x_{2}-x_{3}=2\\ 2x_{1}-x_{2}-3x_{3}=1\\ 3x_{1}+2x_{2}-5x_{3}=0$ , 且 $D=\begin{vmatrix} 1 & -1 & -1\\ 2 & -1 &-3\\3 & 2 & -5 \end{vmatrix}=3\neq 0$ ，

$D_{1}=\begin{vmatrix} 2 & -1 & -1\\ 1 & -1 &-3\\0 & 2 & -5 \end{vmatrix}=15$ ， $D_{2}=\begin{vmatrix} 1 & 2 & -1\\ 2 & 1 &-3\\3 & 0& -5 \end{vmatrix}=0$ ， $D_{3}=\begin{vmatrix} 1 & -1 & 2\\ 2 & -1 &1\\3 & 2 & 0 \end{vmatrix}=9$ ；

所以 $x_{1}=\frac{D_{1}}{D}=5\\ x_{2}=\frac{D_{2}}{D}=0\\ x_{3}=\frac{D_{3}}{D}=3$ .

1.2.3.2 几何意义：三维空间中平行六面体的体积

令 $\vec{m}=(a_{11},a_{12},a_{13})\\ \vec{n}=(a_{21},a_{22},a_{23})\\ \vec{t}=(a_{31},a_{32},a_{33})$ 知 $V=\begin{vmatrix} a_{11} & a_{12}&a_{13}\\ a_{21} & a_{22} &a_{23}\\a_{31}&a_{32}&a_{33} \end{vmatrix}$ ，则可知为向量的混合积（三阶行列式）

即 $(\vec{m}\cdot \vec{n})\times \vec{t}=V$

扩展：

1. 二阶行列式：二维空间中平行四边形面积（若两个二维向量共线，则 $S=0$ ，可以有两行对应成比例这个条件去导致）

2. 三阶行列式：三维空间中平行六面体的体积（若三个三维向量共面，则 $V=0$ ，可以有两行对应成比例这个条件去导致）

3. 四阶行列式：四维空间中平行八面体的 “ 体积 ” （若四个四维向量共面，则 ${}''V{}''=0$ ，可以有两行对应成比例这个条件去导致）

这体现了其线性相关！

（一些说明：

①：有一阶行列式，有 $\begin{vmatrix} a \end{vmatrix}=a,\begin{vmatrix} -a \end{vmatrix}=-a$ ，注意与绝对值的区别（若出现，必有说明!）

②：行列式的行与列的数目是相同的，在矩阵中，其行与列的数目可以不同！）

2. 全排列与对换

2.1 排列的相关概念

2.1.1 排列

由 n 个数1，2，3，......，n 组成的一个有序数组为一个 n 级排列。

例：1，2，3可构成 6 个 3 级排列，如：123，132，213，231，312，321.

故 n 个数可构成 $n!$ 个

（一些说明：

所构成的排列不可缺项，即如：125 这样，必须为12345这5个数字的任意组合。）

2.1.2 顺序

前小后大为顺序；前大后小为逆序。

2.1.3 一个逆序

一对逆序的数字即为一个逆序

例1： $43215$ ， $43$ 构成一个逆序，同理有：42，41，32，31，21，故共有 6 个逆序。

例2： $76814235$ ，共有18个

2.1.4 逆序表

排列的逆序的总数。

找寻方法：①：“ 后面几个小 ” ②：“ 前面几个大 ”

例：对例1有： ① ：3+2+1+0+0=6； ②：0+3+2+1+0=6.

2.1.5 奇偶排列

逆序表为奇数 $\rightarrow$ 奇排序；逆序表为偶数 $\rightarrow$ 偶排列

2.1.6 标准（自然）排列

即：123......n

知其 $N(123......n)=0$ （ $N$ 为逆序表，亦可用 $t$ , $\tau$ 等）

若为 $N\left [ n(n-1)(n-2)....321 \right ]=\frac{n(n-1)}{2}$

例1：已知 n 个数组成的排列 $x_{1}x_{2}x_{3}...x_{n-2}x_{n-1}x_{n}$ 逆序表为 $k$ ，求 $x_{n}x_{n-1}x_{n-2}...x_{3}x_{2}x_{1}$ 的逆序表。

解：方法A：后面几个小：对于 $x_{1}x_{2}x_{3}...x_{n-2}x_{n-1}x_{n}$ 有：

设 $x_{1}$ 后面比 $x_{1}$ 小的有 $k_{1}$ 个，则同理知： $x_{2}$ ..... $k_{2}$ 个 , $x_{3}$ ..... $k_{3}$ 个 , ...... , $x_{n-1}$ ..... $k_{n-1}$ 个 , $x_{n}$ ..... $k_{n}$ 个 , 则共有 $k_{1}+k_{2}+k_{3}+.....+k_{n-1}+k_{n}=k$ ;

方法B：前面几个大：对于 $x_{n}x_{n-1}x_{n-2}...x_{3}x_{2}x_{1}$ 有：

$x_{1}$ 前面比 $x_{1}$ 大的有 $(n-1)-k_{1}$ 个 , $x_{2}$ 前面比 $x_{2}$ 大的有 $(n-2)-k_{2}$ 个 , ...... , $x_{n-1}$ 前面比 $x_{n-1}$ 大的有 $\left [n- (n-1)-k_{n-1} \right ]$ 个 , $x_{n}$ 前面比 $x_{n}$ 大的有 $\left [ (n-n)-k_{n} \right ]$ 个;

则共有： $(n-1)+(n-2)+(n-3)+....+1+0-(k_{1}+k_{2}+....+k_{n})=\frac{n(n-1)}{2}-k$

例2：用排列 $76814235$ 验证例一结论。

解：前面几个大： $0+1+0+3+3+4+4+3=18=k$ ,

知由结论，对于 $53241867$ ，有 $N(53241867)=\frac{8*7}{2}-k=10$ ,

由后面几个小，得： $4+2+1+1+0+2+0+0=10$ ，故得证。

2.2 对换相关概念

2.2.1 对换

排列中任意两数交换位置，其余不变。

2.2.2 相邻对换

相邻两数交换位置，其余不变。

2.2.3 定理一

排列经过一次对换，奇偶性改变。

如 $N(12534)=0+0+0+1+1=2$ , 则 $N(14532)=0+0+0+2+3=5$

推论：奇（偶）排列通过对换的方式变成标准排列，需要对换奇（偶）数次。

如： $123456\Leftrightarrow 126453\Leftrightarrow 426153$

从原偶（标准） $\Leftrightarrow$ 奇 $\Leftrightarrow$ 偶，故。

3. n 阶行列式定义

3.1. 回顾

3.1.1.

$\begin{vmatrix} a_{11} & a_{12}&a_{13}\\ a_{21} & a_{22} &a_{23}\\a_{31}&a_{32}&a_{33} \end{vmatrix}$ 的值为：

$a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}+(-a_{13}a_{22}a_{31})+(-a_{12}a_{21}a_{33})+(-a_{11}a_{23}a_{32})=\sum(-1)^{N}a_{1p1}a_{2p2}a_{3p3}$

$p1p2p3$ 为1，2，3的所有排列； $N$ 为 $p1p2p3$ 的逆序表。

可以观察到：行标排列：123（自然排列），列标排列：有 $"+"$ 的那一行，观察到： $N(123)=0,N(231)=2,N(312)=2$ ，其逆序表皆为偶数，而有 "— "的那一行，观察到： $N(321)=3,N(213)=1,N(132)=1$ ，其逆序表皆为奇数。

3.1.2.

$\begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix}=(+a_{11} *a_{22} )+(-a_{12} *a_{21} )=a_{11} *a_{22} -a_{12} *a_{21}=\sum (-1)^{N}a_{1p1}a_{2p2}$

$p1p2$ 为1，2的所有排列； $N$ 为 $p1p2$ 的逆序表。

可以观察到：行标排列：12（自然排列），列标排列：有 $"+"$ 的那一行，观察到： $N(12)=0$ ，

其逆序表皆为偶数，而有 "— "的那一行，观察到： $N(21)=1$ ，其逆序表皆为奇数。

3.2. n 阶行列式定义（按行定义）

$D=\begin{vmatrix} a_{11} & a_{12} & ...& a_{1n}\\ a_{21} & a_{22} &...&a_{2n}\\...&...&...&...\\a_{n1} & a_{n2} &...& a_{nn} \end{vmatrix}=\sum (-1)^{N}a_{1p1}a_{2p2}...a_{npn}=det(a_{ij})$

其中 $p1p2p3...pn$ 为 $1,2,3,...,n$ 的所有排列， $N$ 为它的逆序表，且共有 $n!$ 个排列

例：判断4阶行列式某些项前的符号

$D=\begin{vmatrix} a_{11} & a_{12} & a_{13}& a_{14}\\ a_{21} & a_{22} &a_{23}&a_{24}\\a_{31}&a_{32}&a_{33}&a_{34}\\a_{41} & a_{42} &a_{43}& a_{44} \end{vmatrix}$

1. $a_{13}a_{22}a_{34}a_{41}$

2. $a_{11}a_{22}a_{33}a_{44}$

3. $a_{13}a_{24}a_{32}a_{41}$

4. $a_{14}a_{23}a_{32}a_{41}$

解：①：+，②：-，③：-，④：+。

3.3 特殊行列式的计算

3.3.1 主对角线行列式

$\begin{vmatrix} a_{11} & 0 & 0& ...&0 \\ 0 & a_{22} &0&...&0 \\0&0&a_{33}&...&0 \\... & ... &...& ...&0 \\0&0&0&...&a_{nn} \end{vmatrix}=+a_{11}a_{22}a_{33}...a_{nn}$ ,共 $n!$ 项。

主上三角：

$\begin{vmatrix} a_{11} & a_{12} & a_{13}& ...&a_{1n} \\ 0 & a_{22} &a_{23}&...&a_{2n} \\0&0&a_{33}&...&a_{3n} \\... & ... &...& ...&a_{(n-1)n} \\0&0&0&...&a_{nn} \end{vmatrix}=+a_{11}a_{22}a_{33}...a_{nn}$

主下三角：

$\begin{vmatrix} a_{11} & 0 & 0& ...&0 \\ a_{21}& a_{22} &0&...&0 \\a_{31}&a_{32}&a_{33}&...&0 \\... & ... &...& ...&0 \\a_{n1}&a_{n2}&a_{n3}&...&a_{nn} \end{vmatrix}=+a_{11}a_{22}a_{33}...a_{nn}$

3.3.2 副对角线行列式

$D=\begin{vmatrix} 0 & ... & 0& a_{1n}\\ 0 & ... &a_{2(n-1)}&0\\...&...&...&...\\a_{n1} & ... &0& 0 \end{vmatrix}=(-1)^{\frac{n(n-1)}{2}}a_{1n}a_{2(n-1)}...a_{n1}$

其中： $N(n(n-1)(n-2)...321)=\frac{n(n-1)}{2}$

同理副上三角：

$\begin{vmatrix} 0 & ... & 0& a_{1n}\\ 0 & ... &a_{2(n-1)}&a_{2n}\\...&...&...&...\\a_{n1} & ... &a_{n(n-1)}& a_{nn} \end{vmatrix}=(-1)^{\frac{n(n-1)}{2}}a_{1n}a_{2(n-1)}...a_{n1}$

副下三角：

$\begin{vmatrix} a_{11} & ... & a_{1(n-1)} & a_{1n}\\ a_{21} & ... &a_{2(n-1)}&0\\...&...&...&...\\a_{n1} & ... &0& 0 \end{vmatrix}=(-1)^{\frac{n(n-1)}{2}}a_{1n}a_{2(n-1)}...a_{n1}$

例1： $\begin{vmatrix} a_{11} & a_{12} & a_{13}& a_{14}&a_{15} \\ a_{21} & a_{22} &a_{23}&a_{24}&a_{25} \\a_{31}&a_{32}&0&0&0\\a_{41} & a_{42}&0& 0&0 \\a_{51}&a_{52}&0&0&0 \end{vmatrix}=0$

例2：证明 $D=\begin{vmatrix} a_{11} & a_{12} & 0& 0\\ a_{21} & a_{22} &0&0\\a_{31}&a_{32}&a_{33}&a_{34}\\a_{41} & a_{42} &a_{43}& a_{44} \end{vmatrix}=\begin{vmatrix} a_{11} & a_{12} \\ a_{21}& a_{22} \end{vmatrix}\begin{vmatrix} a_{33} & a_{34} \\ a_{43} & a_{44} \end{vmatrix}$

证明：将其展开，后提公因式再变换即可。

展开得： $+a_{11}a_{22}a_{33}a_{44}-a_{11}a_{22}a_{34}a_{43}-a_{12}a_{21}a_{33}a_{44}+a_{12}a_{21}a_{34}a_{43}=D$

且变换得： $D=( a_{11}a_{22}-a_{12}a_{21})(a_{33}a_{44}-a_{34}a_{43})=\begin{vmatrix} a_{11} & a_{12} \\ a_{21}& a_{22} \end{vmatrix}\begin{vmatrix} a_{33} & a_{34} \\ a_{43} & a_{44} \end{vmatrix}$

3.4. n 阶行列式其它形式的定义

3.4.1 按列定义

$D=\begin{vmatrix} a_{11} & a_{12} & ...& a_{1n}\\ a_{21} & a_{22} &...&a_{2n}\\...&...&...&...\\a_{n1} & a_{n2} &...& a_{nn} \end{vmatrix}=\sum (-1)^{N}a_{P_{1}1}a_{P_{2}2}...a_{P_{n}n}$

其中 $p1p2p3...pn$ 为 $1,2,3,...,n$ 的所有排列， $N$ 为它的逆序表，且共有 $n!$ 个排列

3.4.2 普通定义

$D=\begin{vmatrix} a_{11} & a_{12} & ...& a_{1n}\\ a_{21} & a_{22} &...&a_{2n}\\...&...&...&...\\a_{n1} & a_{n2} &...& a_{nn} \end{vmatrix}=\sum (-1)^{N_{1}+N_{2}}a_{i_{1}j_{1}}a_{i_{2}j_{2}}...a_{i_{n}i_{n}}$

其中 $i_{1}i_{2}...i_{n}$ 是 $1,2,3...n$ 的所有排列， $N_{1}$ 为它的逆序表；

$j_{1}j_{2}...j_{n}$ 是 $1,2,3...n$ 的所有排列， $N_{2}$ 为它的逆序表；

例1：某四阶行列式某项为 $(-1)^{?}a_{21}a_{4m}a_{t3}a_{n2}$ ，假设元素下标为该元素在行列式中的真实位置，讨论该项前的符号。

解：行排序：24tn； $N_{1}=(1432)=3$ ；

列排序1m32。则知m=4，现在则有①：t=1,n=3;②t=3,n=1

当①： $N_{2}=(2413)=3$ ，所以 $N=N_{1}+N_{2}=6\rightarrow +$

当②： $N_{2}=(2431)=4$ ，所以 $N=N_{1}+N_{2}=7\rightarrow -$

4. 行列式的定义

4.1. 行列互换，其值不变

$D=\begin{vmatrix} a_{11} & a_{12} & a_{13}& a_{14}\\ a_{21} & a_{22} &a_{23}&a_{24}\\a_{31}&a_{32}&a_{33}&a_{34}\\a_{41} & a_{42} &a_{43}& a_{44} \end{vmatrix}=D^{T} =\begin{vmatrix} a_{11} & a_{21} & a_{31}& a_{41}\\ a_{12} & a_{22} &a_{32}&a_{42}\\a_{13}&a_{23}&a_{33}&a_{43}\\a_{14} & a_{24} &a_{34}& a_{44} \end{vmatrix}$

第一种解释：假设如 $D=a+b+c+d+e+f$ ， $D^{T}=b+d+e+f+a+c$ ，

所以 $D=D^{T}$ 。

第二种解释：对 $D$ 抽取一项，有 $(-1)^{N(3241)}a_{13}a_{22}a_{34}a_{41}$ （从上往下写），知 $N(3241)=4\rightarrow +$ ；对 $D^{T}$ 抽取同样一项，但此时其行列下标已不能表示其真实位置，故变换一下，可得：

$a_{41}a_{22}a_{13}a_{34}=b_{14}b_{22}b_{31}b_{43}$ ，可知 $N(4213)=4\rightarrow +$ ，所以 $D=D^{T}$ 。

4.2 对换行列式的其中两行(列)，其余不变，行列式变号

$D_{1}=\begin{vmatrix} a_{11} & a_{12} & a_{13}& a_{14}\\ a_{21} & a_{22} &a_{23}&a_{24}\\a_{31}&a_{32}&a_{33}&a_{34}\\a_{41} & a_{42} &a_{43}& a_{44} \end{vmatrix} D_{2} = \begin{vmatrix} a_{31} & a_{32} & a_{33}& a_{34}\\ a_{21} & a_{22} &a_{23}&a_{24}\\a_{11}&a_{12}&a_{13}&a_{14}\\a_{41} & a_{42} &a_{43}& a_{44} \end{vmatrix}$

得： $D_{1}=-D_{2}$

第一种解释：假设如 $D_{1}=a+b+(-c)+d+(-e)+f$ ， $D_{2}=(-a)+(-b)+c+(-d)+e+(-f)$

所以 $D_{1}=-D_{2}$ 。

第二种解释：

对 $D_{1}$ 抽取一项，有 $(-1)^{N(3142)}a_{13}a_{21}a_{34}a_{42}$ （从上往下写），知 $N(3142)=3\rightarrow -$ ；对 $D_{2}$ 抽取同样一项，但此时其行列下标已不能表示其真实位置，故变换一下，可得：

$a_{34}a_{21}a_{13}a_{42}=b_{14}b_{21}b_{33}b_{42}$ ，可知 $N(4132)=4\rightarrow +$ ，所以 $D_{1}=-D_{2}$ 。

推论：两行（列）相等 $\Rightarrow D=0$ ，因为由此性质，有 $D=-D$ ，所以 $D=0$ .

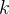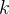4.3 行列式某行(列)有公因子 $k$ ，则 $k$ 可以提到行列式外

$\begin{vmatrix} a_{11} & a_{12}&a_{13}\\ ka_{21} & ka_{22} &ka_{23}\\a_{31}&a_{32}&a_{33} \end{vmatrix}=k\begin{vmatrix} a_{11} & a_{12}&a_{13}\\ a_{21} & a_{22} &a_{23}\\a_{31}&a_{32}&a_{33} \end{vmatrix}=\begin{vmatrix} a_{11} & a_{12}&a_{13}\\ a_{21} & a_{22} &a_{23}\\ka_{31}&ka_{32}&ka_{33} \end{vmatrix}= \begin{vmatrix} a_{11} & ka_{12}&a_{13}\\ a_{21} & ka_{22} &a_{23}\\a_{31}&ka_{32}&a_{33} \end{vmatrix}$

原理： $k(a+b)=ka+kb$

$\begin{vmatrix} a_{11} & a_{12}&a_{13}\\ ka_{21} & ka_{22} &ka_{23}\\a_{31}&a_{32}&a_{33} \end{vmatrix}=ka_{11}a_{22}a_{33}+ka_{12}a_{23}a_{31}+ka_{13}a_{21}a_{32}+(-ka_{13}a_{22}a_{31})+(-ka_{12}a_{21}a_{33})+(-ka_{11}a_{23}a_{32})$

同理： $\begin{vmatrix} ka_{11} & ka_{12} \\ ka_{21} & ka_{22} \end{vmatrix}=k^{2}\begin{vmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{vmatrix}$

$\begin{vmatrix} ka_{11} & ka_{12}&ka_{13}\\ ka_{21} & ka_{22} &ka_{23}\\ka_{31}&ka_{32}&ka_{33} \end{vmatrix}=k^{3}\begin{vmatrix} a_{11} & a_{12}&a_{13}\\ a_{21} & a_{22} &a_{23}\\a_{31}&a_{32}&a_{33} \end{vmatrix}$

4.4 行列式中若两行成比例，则行列式值为0

$\begin{vmatrix} a_{11} & a_{12}&a_{13}\\ ka_{11} & ka_{12} &ka_{13}\\a_{31}&a_{32}&a_{33} \end{vmatrix}=k\begin{vmatrix} a_{11} & a_{12}&a_{13}\\ a_{11} & a_{12} &a_{13}\\a_{31}&a_{32}&a_{33} \end{vmatrix}=0$

4.5 " 相加之分 "

$D=\begin{vmatrix} a_{11} & a_{12}&a_{13}\\ a_{21}+a^{'}_{21} & a_{22}+a^{'}_{22} &a_{23}+a^{'}_{23}\\a_{31}&a_{32}&a_{33} \end{vmatrix}= \begin{vmatrix} a_{11} & a_{12}&a_{13}\\ a_{21} & a_{22} &a_{23}\\a_{31}&a_{32}&a_{33} \end{vmatrix} +\begin{vmatrix} a_{11} & a_{12}&a_{13}\\ a^{'}_{21} & a^{'}_{22} &a^{'}_{23}\\a_{31}&a_{32}&a_{33} \end{vmatrix}$

原理：展开分离相加可变得

单行（列）可折性

$\begin{vmatrix} a+x & b+y \\ c+z & d+w \end{vmatrix}=\begin{vmatrix} a & b \\ c+z & d+w \end{vmatrix}+\begin{vmatrix} x & y \\ c+z & d+w \end{vmatrix}$

$=\begin{vmatrix} a & b \\ c & d \end{vmatrix}+\begin{vmatrix} a & b \\ z & w \end{vmatrix}+\begin{vmatrix} x & y \\ c & d \end{vmatrix}+\begin{vmatrix} x & y \\ z & w \end{vmatrix}$

4.6 将行列式的某一行（列）元素，乘同一数加到另一行（列）对应的元素上，所得新行列式的值等于原行列式

知右边

例： $D=\begin{vmatrix} 3 &1 & -1& 2\\ -5 & 1&3&-4\\2&0&1&-1\\1 & -5&3& -3\end{vmatrix}$

想方设法将其变乘主上三角形式：

①：性质二：第一列与第二列互换：

$=-\begin{vmatrix} 1 &3 & -1& 2\\ 1 & -5&3&-4\\0&2&1&-1\\-5 & 1&3& -3\end{vmatrix}$

②：性质六：第一行乘（-1）加到第二行。得：

$-\begin{vmatrix} 1 &3 & -1& 2\\ 0 & -8&4&-6\\0&2&1&-1\\-5 & 1&3& -3\end{vmatrix}$

第一行乘 5 加到第四行。得：

$-\begin{vmatrix} 1 &3 & -1& 2\\ 0 & -8&4&-6\\0&2&1&-1\\0 & 16&-2& 7\end{vmatrix}$

③：性质二：第二列与第三列互换：

$\begin{vmatrix} 1 &3 & -1& 2\\ 0 & 2&1&-1\\0&-8&4&-6\\0 & 16&-2& 7\end{vmatrix}$

④：性质六：第二行乘 4 加到第三行，第二行乘 -8 加到第四行：

$\begin{vmatrix} 1 &3 & -1& 2\\ 0 & 2&1&-1\\0&0&8&-10\\0 & 0&-10& 15\end{vmatrix}$

再第三行乘 $\frac{10}{8}$ 加到第四行：

$\begin{vmatrix} 1 &3 & -1& 2\\ 0 & 2&1&-1\\0&0&8&-10\\0 & 0&0& \frac{5}{2}\end{vmatrix}$

⑤：得主上三角形式，所以： $1*2*8*\frac{5}{2}=40$ .

4.7 例题

4.7.1 一般变换得

例1： $\begin{vmatrix} 3 &4 & 5& 11\\ 2 & 5&4&9\\5&3&2&12\\14 & -11&21& 29\end{vmatrix}$

解：我们的目标是将其变为上三角或下三角，以便于计算；

将第二行乘（-1）加到第一行，然后得：

$\begin{vmatrix} 1 &-1 & 1& 2\\ 2 & 5&4&9\\5&3&2&12\\14 & -11&21& 29\end{vmatrix}$ ，则此时将第一行乘（-2）（-5）（-14）加到第二，三，四行；得：

$\begin{vmatrix} 1 &-1 & 1& 2\\ 0 & 7&2&5\\0&8&-3&2\\0 & 3&7& 1\end{vmatrix}$ ，则此时第一行/第一列不要再动！

第二行与第四行进行交换，再将第二列与第四列进行交换，得：

$\begin{vmatrix} 1 &2 & 1& -1\\ 0 & 1&7&3\\0&2&-3&8\\0 & 5&2& 7\end{vmatrix}$

此时将第二行乘（-2）（-5）分别加到三，四行，得：

$\begin{vmatrix} 1 &2 & 1& -1\\ 0 & 1&7&3\\0&0&-17&2\\0 & 0&-33& -8\end{vmatrix}$

此时第二行/第二列不要在动！

将三四列互换，完成后，将第三行乘4加到第四行，得：

$\begin{vmatrix} 1 &2 & 1& -1\\ 0 & 1&3&7\\0&0&2&-17\\0 & 0&0& -101\end{vmatrix}$

此时，该行列式已可方便计算。

例 2：

解： $a^{4}$

例2

4.7.2 行/列和相等行列式：

例3： $\begin{vmatrix} 3 &1 & 1& 1\\ 1 & 3&1&1\\1&1&3&1\\1 & 1&1& 3\end{vmatrix}$

解：48

例3

例4： $\begin{vmatrix} x & a & a& ...&a \\ a & x &a&...&a \\a&a&x&...&a \\... & ...&...& ...&... \\a&a&a&...&x \end{vmatrix}$

解： $\left [ x+(n-1)a \right ](x-a)^{n-1}$

例4

例5： $\begin{vmatrix} 1 &-1 & 1& x-1\\ 1 & -1&x+1&-1\\1&x-1&1&-1\\x+1 & -1&1& -1\end{vmatrix}$

解： $x^{4}$

例4

例6：求n+1阶行列式

$\begin{vmatrix} x & a_{1} & a_{1}& ...&a_{n} \\ a_{1} & x &a_{1}&...&a_{n} \\a_{1}&a_{1}&x&...&a_{n} \\... & ...&...& ...&... \\a_{1}&a_{1}&a_{1}&...&x \end{vmatrix}$

解： $(x+\sum_{i=1}^{n}a_{i})\prod_{i=1}^{n}(x-a_{i})$

例6

4.7.3 爪型行列式：

例7： $D_{n+1}=\begin{vmatrix} 1 & a_{1} & a_{2}& ...&a_{n} \\ a_{1} & 1 &0&...&0 \\a_{2}&0&1&...&0 \\... & ...&...& ...&... \\a_{n}&0&0&...&1 \end{vmatrix}$

用斜爪消平爪：

解： $1-\sum_{i=1}^{n}a^{2}_{i}$

4.7.3

例8： $\begin{vmatrix} 1 &1 & 1& 1\\ 1 & 2&0&0\\1&0&3&0\\1 & 0&0& 4\end{vmatrix}$

解：-2

4.7.3

例9： $D_{n+1}=\begin{vmatrix} a_{1} & 0 & ...& 0&c_{1} \\ 0 & a_{2} &...&0&c_{2} \\...&...&...&...&... \\0 & 0&...& a_{n}&c_{n} \\b_{1}&b_{2}&...&b_{n}&a_{n+1} \end{vmatrix}$

其中 $a_{i}\neq 0,i=1,2,3,...,n$ .

解： $(\prod_{i=1}^{n}a_{i})(a_{n+1}-\sum_{i=1}^{n}\frac{b_{i}c_{i}}{a_{i}})$

4.7.3

4.8 拉普拉斯展开式

n+k阶：

$D=\begin{vmatrix} a_{11} &... & a_{1k}& 0&...&0\\ ... & ...&...&0&...&0\\a_{k1}&...&a_{kk}&0&...&0\\c_{11} & ...&c_{1k}& b_{11}&...&b_{1n}\\...&...&...&...&...&...\\c_{n1}&...&c_{nk}&b_{n1}&...&b_{nn}\end{vmatrix}$

$D_{1}=\begin{vmatrix} a_{11} & ...&a_{1k}\\ ... & ...&...\\a_{k1}&...&a_{kk} \end{vmatrix}$ ， $D_{2}=\begin{vmatrix} b_{11} & ...&b_{1k}\\ ... & ...&...\\b_{k1}&...&b_{kk} \end{vmatrix}$

证明： $D=D_{1}D_{2}$

简易想象证明如下：利用二阶行列式而进行的想象证明：

$\begin{vmatrix} A_{k\times k} & 0 \\ C & B_{n\times n} \end{vmatrix}= \left | A_{k\times k} \right |\left | B_{n\times n} \right |= \begin{vmatrix} A_{k\times k} & C \\ 0 & B_{n\times n} \end{vmatrix}= \begin{vmatrix} A_{k\times k} & 0 \\ 0 & B_{n\times n} \end{vmatrix}$

注意不是绝对值，是行列式。

$\begin{vmatrix}0 & A_{k\times k} \\ B_{n\times n} & C \end{vmatrix}= \begin{vmatrix}C & A_{k\times k} \\ B_{n\times n} & 0 \end{vmatrix}= \begin{vmatrix}0 & A_{k\times k} \\ B_{n\times n} & 0 \end{vmatrix}=$

$(-1)^{kn}\left | A_{k\times k} \right |\left | B_{n\times n} \right |$

例1： $D_{1}=\begin{vmatrix} 1 & 4 & 0& 0&0 \\ 3 & 14 &0&0&0\\7&6&5&2&1 \\4 & 7&1& 2&5 \\5&3&34&1&34 \end{vmatrix}$

$D_{2}=\begin{vmatrix} 0 & 0 & 0& 2&4 \\ 0 & 0 &0&1&3\\5&1&2&4&7 \\1 & 2&5& 3&8 \\34&1&34&2&7 \end{vmatrix}$

解：均：1040.

例2： $D_{4}\begin{vmatrix} a &0 & 0& b\\ 0 & a&b&0\\0&c&d&0\\c & 0&0& d\end{vmatrix}$

解： $(ad-bc)^{2}$

例3：计算2n阶行列式：

$D_{2n}=\begin{vmatrix} a &0 & 0& 0&0&b\\ 0 & ...&0&0&...&0 \\0&0&a&b&0&0 \\0 & 0&c& d&0&0 \\0&...&0&0&...&0 \\c&0&0&0&0&d\end{vmatrix}_{2n\times 2n}$

由上题可以进行猜想得其结果为： $D_{2n}=(ad-bc)^{n}$ .

采用递推法：

略。

回到开头：

$D_{1}=\begin{vmatrix} a_{11} & ...&a_{1k}\\ ... & ...&...\\a_{k1}&...&a_{kk} \end{vmatrix}$ ， $D_{2}=\begin{vmatrix} b_{11} & ...&b_{1k}\\ ... & ...&...\\b_{k1}&...&b_{kk} \end{vmatrix}$

证明： $D=D_{1}D_{2}$

（注：任何行列式都可以仅通过行/列变换为上/下三角行列式）

证明如下：

行变换：

$D_{1}\Rightarrow\begin{vmatrix} P_{11} & ...&0\\ ... & ...&...\\P_{k1}&...&P_{kk} \end{vmatrix}=P_{11}...P_{kk}$

列变换：

$D_{2}\Rightarrow\begin{vmatrix} q_{11} & ...&0\\ ... & ...&...\\q_{n1}&...&q_{nn} \end{vmatrix}=q_{11}...q_{nn}$

$D=\begin{vmatrix} P_{11} &... & 0& 0&0&0\\ ... & ...&...&0&0&0 \\P_{k1}&...&P_{kk}&0&0&0 \\C_{11} & ...&C_{1k}& q_{11}&...&0 \\...&...&...&...&...&... \\C_{n1}&...&C_{nk}&q_{n1}&...&q_{nn}\end{vmatrix}$

$=P_{11}...P_{kk}q_{11}...q_{nn}=D_{1}D_{2}$

4.9 对称行列式与反对称行列式

4.9.1 对称

$\begin{vmatrix} x & a&b \\ a & x&c\\b&c&x \end{vmatrix}$

知有 $a_{ij}=a_{ji}$

4.9.2 反对称

满足 $a_{ij}=-a_{ji}$ ，则 $a_{ii}=-a_{ii}$ ，所以 $a_{ii}=0$ .

$D=\begin{vmatrix} 0 & a&-b \\ -a & 0&c\\b&-c&0 \end{vmatrix}$

对其进行转置，有

$D^{T}=\begin{vmatrix} 0 & -a&b \\ a & 0&-c\\-b&c&0 \end{vmatrix}$

可知当前 $D^{T}$ 为 $D$ 的（-1）的奇次方，即 $D^{T}$ 乘（-1）奇数阶即为 $D$ ，又知 $D=D^{T}$ ，

所以D=0.

故可知奇数阶反对称行列式为0.

5. 行列式按行/列展开

（计算行列式的全新方法）

5.1：余子式：

将行列式某元素所在行和列的元素全去掉，剩余部分所构成的行列式，称为该元素的余子式。

$D=\begin{vmatrix} a_{11} & a_{12} & a_{13}& a_{14}\\ a_{21} & a_{22} &a_{23}&a_{24}\\a_{31}&a_{32}&a_{33}&a_{34}\\a_{41} & a_{42} &a_{43}& a_{44} \end{vmatrix}$

其中的 $a_{32}$ 余子式为 $M_{32}=\begin{vmatrix} a_{11} & a_{13}&a_{14}\\ a_{21} & a_{23} &a_{24}\\a_{31}&a_{33}&a_{34} \end{vmatrix}$ ， $a_{24}$ 余子式为 $M_{24}=\begin{vmatrix} a_{11} & a_{12}&a_{13}\\ a_{31} & a_{32} &a_{33}\\a_{41}&a_{42}&a_{43} \end{vmatrix}$

5.2：代数余子式：

规定：如 $a_{32}$ 代数余子式为 $A_{32}=(-1)^{3+2}M_{32}$ ， $a_{24}$ 代数余子式为 $A_{24}=(-1)^{2+4}M_{24}$

5.3：引理：

n 阶行列式，若第 i 行除（i，j）元素都为 0 ，则该行列式等于 $a_{ij}$ 与其代数余子式的乘积。即 $D=(-1)^{j-1+i-1}D_{1}$

$D=\begin{vmatrix} a_{11} & ... &a_{1j} & ...&a_{1n} \\ ... & ... &...&...&...\\0&...&a_{ij}&...&0 \\... & ...&...& ...&...\\a_{n1}&...&a_{nj}&...&a_{nn} \end{vmatrix}=a_{ij}A_{ij}=a_{ij}(-1)^{i+j}M_{ij}$

证明从略：

5.3

例1：

$D=\begin{vmatrix} 4 & 3 & 1\\ 0 & 0 &2\\1 & 7 & 2 \end{vmatrix}$

解：-50

例2：

$D=\begin{vmatrix} 0 & 1 & 2\\ 0 & 3 &4\\1 & 7 & 6 \end{vmatrix}$

解：-8

例3：

$D=\begin{vmatrix} 0 &2 & 1& 3\\ 0 & 2&6&7\\2&0&3&7\\0 & 0&3& 0\end{vmatrix}$

解：-48

5.3

5.4 定理2（行列式按行/列展开法则）

行列式等于它的任一行/列的各元素与对应代数余子式乘积之和

$D=\begin{vmatrix} a_{11} & a_{12} & ...&a_{1n} \\ ...& ... &...&...\\a_{i1} & a_{i2} & ...&a_{in} \\ ...&...&...&...\\ a_{n1}&a_{n2}&...&a_{nn}\end{vmatrix}=a_{i1}A_{i1}+a_{i2}A_{i2}+...+a_{in}A_{in}$

证明从略：

5.4

辩析： $D_{1}$ 和 $D_{2}$ 中 $a_{i1}$ 的代数余子式有无区别？

$D_{1}=\begin{vmatrix} a_{11} & a_{12} & ...&a_{1n} \\ ...& ... &...&...\\a_{i1} & a_{i2} & ...&a_{in} \\ ...&...&...&...\\ a_{n1}&a_{n2}&...&a_{nn}\end{vmatrix}$

$D_{2}=\begin{vmatrix} a_{11} & a_{12} & ...&a_{1n} \\ ...& ... &...&...\\a_{i1} & 0 & ...&0 \\ ...&...&...&...\\ a_{n1}&a_{n2}&...&a_{nn}\end{vmatrix}$

解：动用公式，无区别，故其代数余子式可用同一符号。

5.5 例题

例1：

$D=\begin{vmatrix} 2 &-1 & 0& 0\\ 0 & 2&-1&0\\0&0&2&-1\\-1 & 0&0& 2\end{vmatrix}$

解：15

原则：选则含0量较高的行/列展开

例2：

$D=\begin{vmatrix} \lambda &-1 & 0& 0\\ 0 & \lambda &-1&0\\0&0&\lambda &-1\\4 & 3&2& \lambda +1\end{vmatrix}$

解：异爪型：

$4+3\lambda +2\lambda ^{2}+\lambda ^{3}+\lambda ^{4}$

例3：

$D=\begin{vmatrix} 3 &1 & -1& 2\\ -5 & 1&3&-4\\2&0&1&-1\\1 & -5&3& -3\end{vmatrix}$

解：40

例4：

$D=\begin{vmatrix} 3 &4 & 5& 11\\ 2 & 5&4&9\\5&3&2&12\\14 & -11&21& 29\end{vmatrix}$

解：202

5.5

5.6 行列式按行/列展开的逆向运用

5.6.1 运用加边法求解行列式

$D_{n+1}=\begin{vmatrix} 1 & ? &? & ...&? \\ 0 & a_{11}&a_{12}&...&a_{1n} \\0&a_{21}&a_{22}&...&a_{2n} \\... & ...&...& ...&... \\0&a_{n1}&a_{n2}&...&a_{nn} \end{vmatrix}=1\cdot (-1)^{1+1}\begin{vmatrix} a_{11}& ... & a_{1n}\\ ... & ... &...\\a_{n1} & ... & a_{nn} \end{vmatrix}$

即容易 $\rightleftharpoons$ 难算

例1：

$D_{n}=\begin{vmatrix} 1+x_{1}^{2} &x_{1}x_{2} & ...& x_{1}x_{n}\\ x_{2}x_{1} & 1+x_{2}^{2}&...&x_{2}x_{n}\\...&...&...&...\\x_{n}x_{1} & x_{n}x_{2}&...& 1+x_{n}^{2}\end{vmatrix}$

解： $1+\sum_{i=1}^{n}x_{i}^{2}$

例2： $D_{n}=$

$\begin{vmatrix} a_{1}+x_{1}& a_{2} & ...& a_{n}\\ a_{1} & a_{2}+ x_{2}&...& a_{n}\\...&...&...&...\\ a_{1} & a_{2}& ...& a_{n}+ x_{n}\end{vmatrix}$

解：

$(1+\sum_{i=1}^{n}\frac{a_{i}}{x_{i}})(\prod_{i=1}^{n}x_{i})$

5.6.1

5.6.2 求余子式/代数余子式之和

例1：写出其代数余子式之和

$D_{1}=\begin{vmatrix} 3 &7 & 8& 4\\ 2 & 6&1&6\\1&4&3&2\\4 & 1&8& 9\end{vmatrix}$

$D_{2}=\begin{vmatrix} 3 &7 & 8& 4\\ 2 & 6&1&6\\2&8&1&2\\4 & 1&8& 9\end{vmatrix}$

$D_{3}=\begin{vmatrix} 3 &7 & 8& 4\\ 2 & 6&1&6\\7&-6&2&3\\4 & 1&8& 9\end{vmatrix}$

解：易

行列式按列收拢即代数余子式之和变为行列式

例2：

$D=\begin{vmatrix} 3 &-5 & 2& 1\\ 1 & 1&0&-5\\-1&3&1&3\\2 & -4&-1& -3\end{vmatrix}$

D的 $(i,j)$ 元素余子式和代数余子式记作 $M_{ij}$ 和 $A_{ij}$

求 $A_{11}+A_{12}+A_{13}+A_{14},M_{11}+M_{12}+M_{13}+M_{14},2A_{11}-4A_{12}-A_{13}-3A_{14}$

5.6.3 推论：

行列式某行元素与其它行对应元素的代数余子式相乘，然后相加，最后结果必为0（对列也成立）

$D=\begin{vmatrix} 8 &4 & -1& 2\\ 6 & 3&2&7\\7&5&7&2\\2 & -3&9& 6\end{vmatrix}$

如 $8A_{41}+4A_{42}-A_{43}+2A_{44}=0$

（因为将其收拢后，会有两行一样的，故）

例：已知

$D=\begin{vmatrix} 2 &2 & 2& 2\\ a_{21} & a_{22}&a_{23}&a_{24}\\a_{31}&a_{32}&a_{33}&a_{34}\\a_{41} & a_{42}&a_{43}& a_{44}\end{vmatrix}=a$

求 $\sum_{i=1}^{4}\sum_{j=1}^{4}A_{ij}$

解：a/2

5.6.3

6. 范德蒙德行列式

$D=\begin{vmatrix} 1 & 1 &...&1 \\ x_{1}^{}& x_{2}^{}&...& x_{n}^{}\\ x_{1}^{2} & x_{2}^{2} & ...&x_{n}^{2} \\ ...&...&...&...\\ x_{1}^{n-1}&x_{2}^{n-1}&...&x_{n}^{n-1}\end{vmatrix}=\prod (x_{i}-x_{j})(1\leqslant j<i\leqslant n)$

证明：加边法+数学归纳法

如：

$D=\begin{vmatrix} 1 & 1 &1&1 \\ x_{1}^{}& x_{2}^{}&x_{3}^{}& x_{4}^{}\\ x_{1}^{2} & x_{2}^{2} & x_{3}^{2}&x_{4}^{2} \\ x_{1}^{3}&x_{2}^{3}&x_{3}^{3}&x_{4}^{3}\end{vmatrix}$

其结果为： $(x_{4}-x_{3})(x_{4}-x_{2})(x_{4}-x_{1})(x_{3}-x_{2})(x_{3}-x_{1})(x_{2}-x_{1})$

即： $\prod (x_{i}-x_{j})(1\leqslant j<i\leqslant 4)$

又有：

$D=\begin{vmatrix} 1 & 1 &...&1 \\ x_{2}^{}& x_{2}^{}&...& x_{n}^{}\\ x_{2}^{2} & x_{2}^{2} & ...&x_{n}^{2} \\ ...&...&...&...\\ x_{2}^{n-1}&x_{2}^{n-1}&...&x_{n}^{n-1}\end{vmatrix}=\prod (x_{i}-x_{j})(2\leqslant j<i\leqslant n)$

例1：

$D=\begin{vmatrix} 1 &1 & 1& 1\\ 2 & -2&1&-1\\4&4&1&1\\8 & -8&1& -1\end{vmatrix}$

解：72

例2：

解：

$\prod (x_{i}-x_{j})(1\leqslant j<i\leqslant n)$

例3：

$D=\begin{vmatrix} 1 & 1 & 1\\ x_{1} & x_{2} &x_{3}\\x_{1}^{3} & x_{2}^{3} & x_{3}^{3} \end{vmatrix}$

解： $(\sum_{i=1}^{3}x_{i})\left [ \prod (x_{i}-x_{j}) \right ]$ ，

$(1\leqslant j<i\leqslant 3)$

练习：

$D=\begin{vmatrix} 1 & 1 & 1&1&1\\ x_{1}^{} & x_{2}^{} &x_{3}^{}&x_{4}^{}&x_{5}^{} \\ x_{1}^{2} & x_{2}^{2} & x_{3}^{2} &x_{4}^{2} &x_{5}^{2} \\x_{1}^{3}&x_{2}^{3}&x_{3}^{3}&x_{4}^{3}&x_{5}^{3} \\x_{1}^{5}&x_{2}^{5}&x_{3}^{5}&x_{4}^{5}&x_{5}^{5} \end{vmatrix}$

解： $D=(\sum_{i=1}^{5})(\prod (x_{i}^{}-x_{j}^{} )(1\leqslant j<i\leqslant 5))$

7. 用递推法求行列式

例1：

$D_{n}=\begin{vmatrix} 2 &-1& 0& ...&0&0\\-1& 2&-1&...&0&0 \\0&-1&2&...&0&0 \\... & ...&...& ...&...&... \\0&0&0&...&2&-1\\0&0&0&...&-1&2\end{vmatrix}$

解：n + 1

例2：

$D_{n}=\begin{vmatrix} 5 &3& 0& ...&0&0\\2& 5&3&...&0&0 \\0&2&5&...&0&0 \\... & ...&...& ...&...&... \\0&0&0&...&5&3\\0&0&0&...&2&5\end{vmatrix}$

解： $3^{n+1}-2^{n+1}$

例3：

解：当 $\alpha \neq \beta$ 时，为 $\frac{\alpha^{n+1} -\beta^{n+1}}{\alpha -\beta}$ ， $\alpha =\beta$ 时，为 $(n+1)\alpha ^{n}$ .

例4：

$D_{n}=\begin{vmatrix} a_{1} &-1& 0& ...&0&0\\a_{2}& x_{}&-1&...&0&0 \\a_{3}&0&x&...&0&0 \\... & ...&...& ...&...&... \\a_{n-1}&0&0&...&x&-1\\a_{n}&0&0&...&0&x\end{vmatrix}$

解：异爪型：

$D_{n}=a_{n}+xa_{n-1}+x^{2}a_{n-2}+...+x^{n-2}a_{2}+x^{n-1}a_{1}$

8. 用数学归纳法证明行列式

8.1 第一种

①：第一个正确；

②：前一个正确 $\Rightarrow$ 后一个正确

由①② $\Rightarrow$ 所有都正确。

8.2 第二种

①：第1，2个正确；

②：前两个正确 $\Rightarrow$ 后一个正确

由①② $\Rightarrow$ 所有都正确。

8.3 证明范德蒙德行列式

证明从略。

例1：

证明：

$D_{n}=\begin{vmatrix} 2a &1& 0& ...&0&0\\a^{2}& 2a&1&...&0&0 \\0&a^{2}&2a&...&0&0 \\... & ...&...& ...&...&... \\0&0&0&...&2a&1\\0&0&0&...&a^{2}&2a\end{vmatrix}=(n+1)a^{n}$