前言
该文章是何凯明组发表于CVPR2021上的文章,目前已获得最佳论文提名,主要解决自监督对比学习中的奔溃解问题。奔溃解即不论什么输入,特征提取器输出的特征向量都相同。
本文将简单介绍SimSiam,记录其中较有意思的实验结果。
作者并没有解释为什么SimSiam可以避免奔溃解,但文章的确非常出彩
SimSiam简述
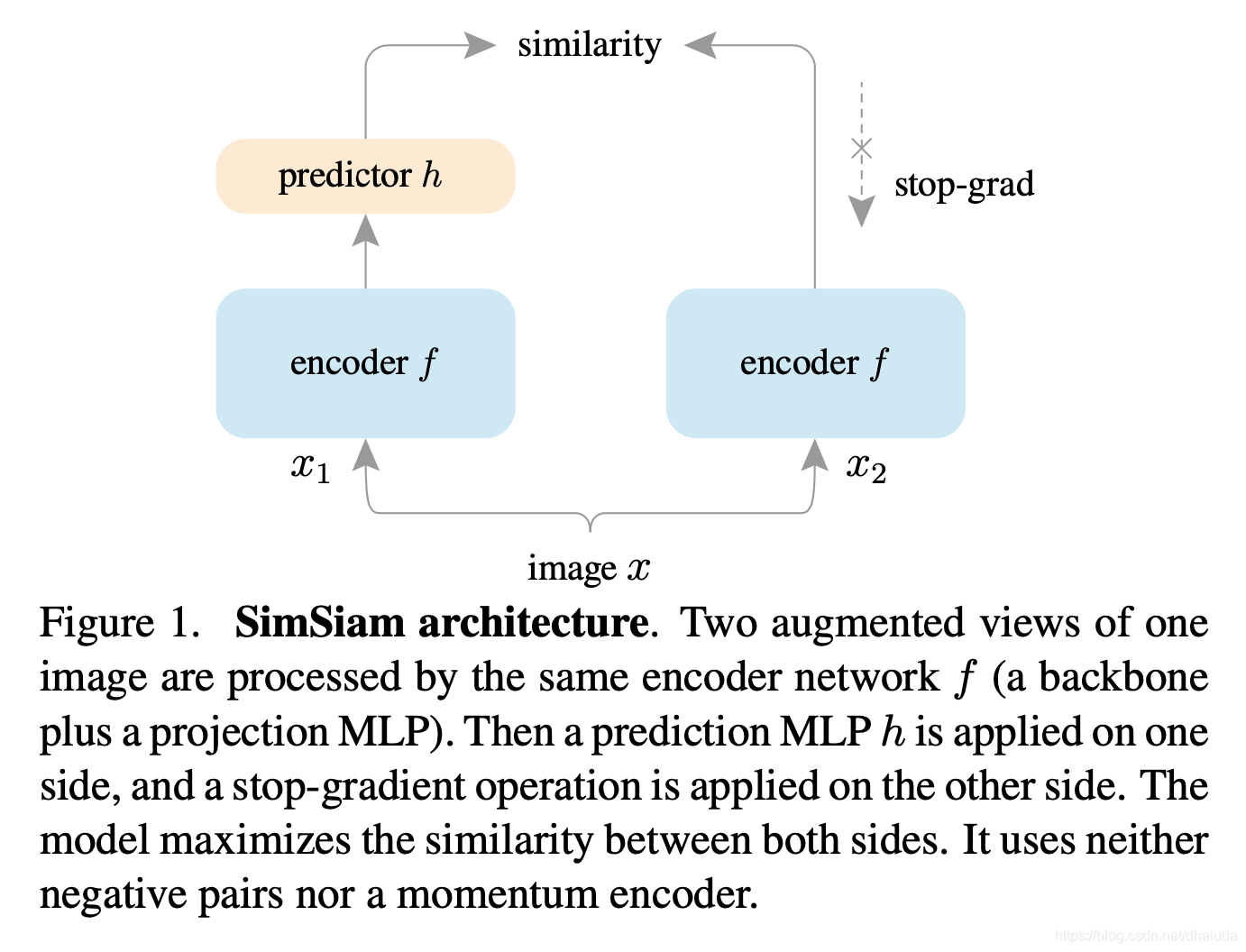
上图即SimSiam的整体结构,具体而言
- 对输入图像x施加数据增强,得到 x 1 x_1 x1、 x 2 x_2 x2
- 将 x 1 x_1 x1、 x 2 x_2 x2输入到同一个特征提取器中,并经过一个projection MLP处理得到 z 1 z_1 z1、 z 2 z_2 z2
- z 1 z_1 z1经过prediction MLP处理,得到 p 1 p_1 p1
对比学习的loss为
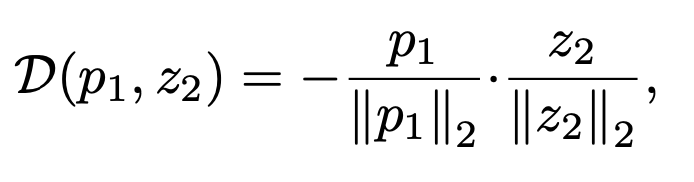
反向传播时,
z
2
∣
∣
z
2
∣
∣
2
\frac{z_2}{||z_2||_2}
∣∣z2∣∣2z2会被看成为常数,只有
p
1
∣
∣
p
1
∣
∣
2
\frac{p_1}{||p_1||_2}
∣∣p1∣∣2p1会产生梯度,可以看到奔溃解是存在于解空间中的。
作者有对上述优化过程做一个解释,假设我们的损失函数为
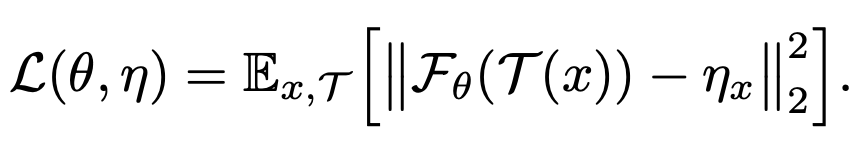
F
θ
(
x
)
F_\theta(x)
Fθ(x)为神经网络,
T
(
x
)
T(x)
T(x)表示对数据x做数据增强,
η
x
\eta_x
ηx可看成是一个待估参数,上述式子的待估参数为
θ
\theta
θ、
η
x
\eta_x
ηx,loss最小化的具体优化过程类似于坐标下降法,如下所示
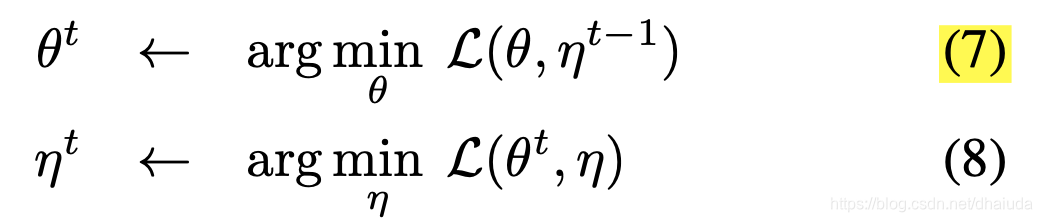
η
t
−
1
\eta^{t-1}
ηt−1表示t-1次优化后,
η
\eta
η的值,
θ
t
\theta^t
θt同理,首先将
η
t
−
1
\eta^{t-1}
ηt−1看成常数,求得
θ
t
\theta^{t}
θt,在所有
θ
\theta
θ取值中,
L
(
θ
t
,
η
t
−
1
)
L(\theta^t,\eta^{t-1})
L(θt,ηt−1)取值将为最小,同理可求得
η
t
\eta^t
ηt,其实就是坐标下降法。
η
t
\eta^t
ηt的数学表达式可以通过下式求得
∂
L
(
θ
,
η
)
∂
η
=
−
E
T
[
2
(
F
θ
t
(
T
(
x
)
)
−
η
x
)
]
=
0
\frac{\partial L(\theta,\eta)}{\partial \eta}=-E_T[2(F_{\theta^t}(T(x))-\eta_x)]=0
∂η∂L(θ,η)=−ET[2(Fθt(T(x))−ηx)]=0
解得
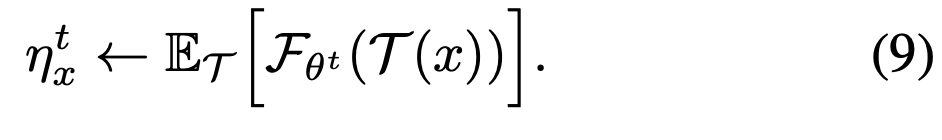
通过蒙特卡洛近似,我们以一个样本做近似可得
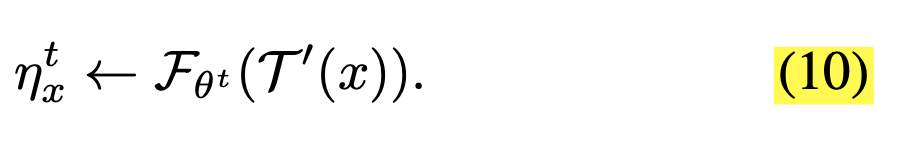
T
′
(
x
)
T'(x)
T′(x)表示对x施加数据增强,和
T
(
x
)
T(x)
T(x)是一样的,这么写有助于后续的数学表达式书写,将上述式子代入式7中可得
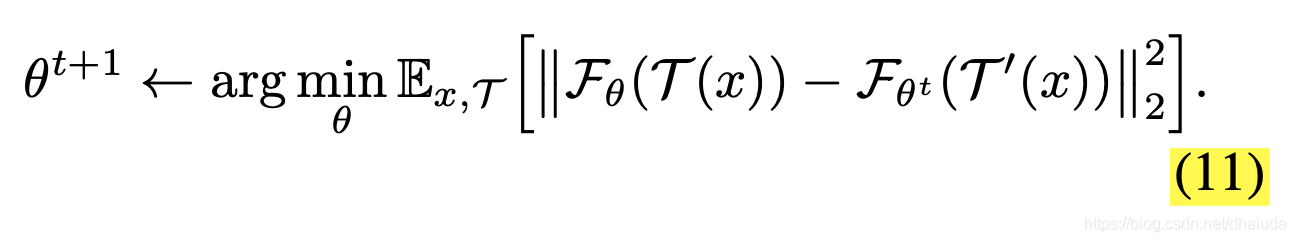
上述式子可以看成对一张图片 x x x施加两次数据增强,得到 T ( x ) 、 T ′ ( x ) T(x)、T'(x) T(x)、T′(x),经过神经网络处理后,在特征空间做L2距离,反向传播时, F θ t ( T ′ ( x ) ) F_{\theta^t}(T'(x)) Fθt(T′(x))看成为常数。当 F θ t ( T ′ ( x ) ) 、 F θ ( T ( x ) ) F_{\theta^t}(T'(x))、F_{\theta}(T(x)) Fθt(T′(x))、Fθ(T(x))经过L2归一化后,上述式子可以与SimSiam的loss做一个等价。
因此,SimSiam可以看成是一个含有两个待估参数集的优化问题。为了验证该假设,作者做了一组实验,如下所示
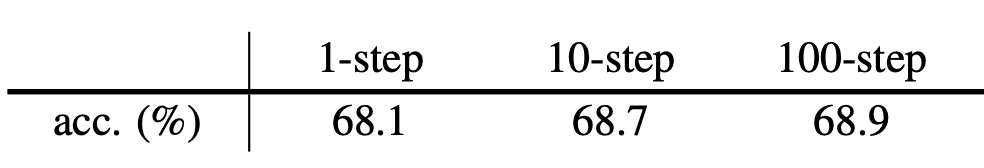
k-step表示先存储
k
k
k个
F
θ
t
(
T
′
(
x
)
)
F_{\theta^t}(T'(x))
Fθt(T′(x)),将其看成常数,对式11中的
F
θ
(
T
(
x
)
)
F_{\theta}(T(x))
Fθ(T(x))进行k次梯度更新得到
θ
t
+
k
\theta^{t+k}
θt+k,类似于优化式7.0。接着优化
η
\eta
η,即将
F
θ
(
T
(
x
)
)
F_{\theta}(T(x))
Fθ(T(x))看成常数,对式11中的
F
θ
t
+
k
(
T
′
(
x
)
)
F_{\theta^{t+k}}(T'(x))
Fθt+k(T′(x))进行梯度更新,类似于优化式8.0。可以看到,优化结果非常好,证明了作者的假设。
上述过程中,我故意省去了prediction MLP,由于式10.0是对式9.0的粗略估计,因此作者假设prediction MLP弥补了粗略估计带来的误差,并通过实验进行了验证,在此不做记录。
算法伪代码如下

实验
此处不记录验证SimSiam可以避免奔溃解的有关实验,只记录一些有助于实践的实验结果
SimSiam是不需要负例的对比学习算法,因此其对batch size的大小是不敏感的,如下所示

除此之外,作者验证了prediction MLP的作用,如下所示,可见prediction MLP对于SimSiam的影响非常大

除此之外,作者还探究了在prediction MLP和projection MLP的输出层添加BN的影响,如下所示,BN层对SimSiam的影响也如此显著(捂脸),看起来对比学习对于一些细节操作异常敏感。























 483
483











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








