SVM的理解和推导(线性)

本文参考了一些日语的课件，所以图片上会出现一些日文，但结合注解看的话问题不是很大

---

一、问题引入

二、拉格朗日乘数法

2-1 求最优解问题

对于$f(x)$，如果我们想求解 $maximizef(x)$，那么我们需要找到$\nabla f=0$ 对应的数据点，大多数情况下，$x$都是多维数据，以$n$维为例，这里$\nabla f$可以表示为：
$$\nabla f=\left[\begin{array}{c}\frac{\partial f}{\partial x_1}\\ ...\\ \frac{\partial f}{\partial x_n}\end{array}\right]=0$$
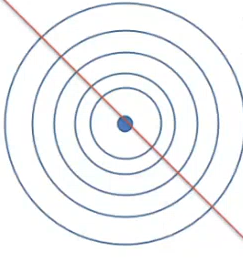
下图用圆环表示某二次函数的俯视图，其中圆心表示梯度为0的点，也就是我们要求的最优解对应的$x$

2-2 条件限制下 求最优解问题

一般情况下，在求解$maximizef(x)$的同时都会有条件限制，比如$g(x)=0$，该条件可以是线性也可以是非线性，线性条件如下图所示：

左边是限制条件不包含最优解的情况，而右边是限制条件刚好包含最优解的情况。

那么在条件限制情况下，什么时候能够达到最优解，下图中蓝色箭头表示原函数的梯度，粉色箭头表示限制条件的梯度：

这里我们以线性的$g(x)$为例，我们可以观察到在切线处的梯度为0，也就是
$\nabla f(x)+\nabla g(x)=0$，同时我们也可以观察到在这个点上，不论$g(x)$如何变化改点梯度始终为0，但由于这里$g(x)$是线性的，所以梯度在哪里都一样，不太容易理解，如果是非线性的话，不同点梯度是不一样的，但我们仍要找到某一个$x$，使得$g(x)$无论怎么变化，两函数梯度之和为0，因此，我们需要找到$x$满足以下条件：
$$\nabla f(x)+\lambda \nabla g(x)=0$$

2-3 拉格朗日函数

由此我们引出拉格朗日函数，其中$\lambda$称为拉格朗日乘数
$$L(x,\lambda )=f(x)+\lambda g(x)$$

两边同时对$x$求偏导，我们可以得到最优解条件：
$${\nabla }_{x}L={\nabla }_{x}f+\lambda {\nabla }_{x}g=0$$

两边同时对$\lambda$求偏导，我们可以得到限制条件：
$${\nabla }_{\lambda }L=g(x)=0$$

综上，对于求解限制条件下的最优解的问题，可以简化为下式：
$$\left[\begin{array}{c}{\nabla }_{x}L\\ {\nabla }_{\lambda }L\end{array}\right]=\left[\begin{array}{c}0\\ 0\end{array}\right]$$

2-4 不等式限制条件

上述都是等式限制条件，但事实上存在很多不等式限制条件如 $g(x)\ge 0$，这个时候我们分3种情况讨论：

1. 一种是$g(x)>0$，此时我们称之为无效限制条件，即$\lambda =0$，等同于$\nabla f(x)=0$

2. 另一种情况是$g(x)=0$，此时我们回归到等式限制条件，用通常的拉格朗日乘数法求解，即$\nabla L=\nabla f+\lambda \nabla g=0$，同时$\lambda >0$

3. 另外对于$g(x)<0$，我们同样将其视为等式限制条件

由此我们可以归纳得到KKT条件，即对于$g(x)\ge 0$的限制条件，要使$f(x)$最大化，需要满足下列条件：
$$g(x)\ge 0$$ $$\lambda \ge 0$$ $$\lambda g(x)=0$$

三、支持向量机 SVM

3-1 定义

SVM是一种在分类问题中求最佳决策平面的算法，该决策面满足，到距离最近的几个样本点的距离之和最大，注意是最近的几个样本点，不同决策面有不同的最近样本点，这几个样本到决策面的距离是一样的，并且也是最小的，因此存在这样一个决策面，使得最近几个样本点到决策面距离之和最大。如下图所示，距离该决策面最近的3个样本点是2个红点1个蓝点，其中$x_1$，$x_2$表示数据是二维的，大多数情况下数据都是高维的，为了表示方便这里只用2维数据，这3个最近的样本点也被称为支持向量，在平面上每个数据都是由向量表示的，下图中
サポートベクター = 支持向量
決定面 = 决策面
マージン = 距离

3-2 推导

下面定义几个变量方便后面的推导：

$N$ 个输入数据（向量）: $x_1,x_2,x_3..,x_N$
数据对应的标签：$t_1,t_2,t_3,...,t_N$ 其中 t ∈ { − 1 , 1 } t\in\{-1,1\} t∈{ −1,1}
决策面： $y(x)=w^{T}x+b=0$ 其中$w$和$b$是需要调整优化的参数
正确的识别函数需要满足：$t_{n}y(x_n)>0$

先考虑如何计算离决策面最近几个样本点距离之和，直接能想到的就是把所有数据点到决策面的距离都算一次，找最小的几个，再求和，那么我们先表示出任意一点到决策面的距离：