模型融合---Xgboost总结

一、简介

全称：eXtreme Gradient Boosting

作者：陈天奇

基础：GBDT

所属：boosting迭代型、树类算法

适用范围：回归，分类，排序

xgboost工具包：sklearn xgboost链接 | xgboost工具包(中文)链接 | xgboost工具包(英文)链接

论文链接 | 项目地址 | ppt

优点：

• 显示的把树模型复杂度作为正则项加到优化目标中。
• 公式推导中用到了二阶导数，用了二阶泰勒展开。
• 实现了分裂点寻找近似算法。
• 利用了特征的稀疏性。
• 数据事先排序并且以block形式存储，有利于并行计算。
• 基于分布式通信框架rabit，可以运行在MPI和yarn上。
• 实现做了面向体系结构的优化，针对cache和内存做了性能优化。

缺点：（与LightGBM相比）

• XGBoost采用预排序，在迭代之前，对结点的特征做预排序，遍历选择最优分割点，数据量大时，贪心法耗时，LightGBM方法采用histogram算法，占用的内存低，数据分割的复杂度更低；
• XGBoost采用level-wise生成决策树，同时分裂同一层的叶子，从而进行多线程优化，不容易过拟合，但很多叶子节点的分裂增益较低，没必要进行跟进一步的分裂，这就带来了不必要的开销；LightGBM采用深度优化，leaf-wise生长策略，每次从当前叶子中选择增益最大的结点进行分裂，循环迭代，但会生长出更深的决策树，产生过拟合，因此引入了一个阈值进行限制，防止过拟合；

二、Xgboost

1.损失函数

xgboost 也是使用与提升树相同的前向分步算法。其区别在于：xgboost 通过结构风险极小化来确定下一个决策树的参数 ：

最初损失函数：

$L_t=\sum\limits_{i=1}^mL(y_i, f_{t-1}(x_i)+ h_t(x_i)) + \gamma J + \frac{\lambda}{2}\sum\limits_{j=1}^Jw_{tj}^2$ 

在GBDT损失函数$L(y, f_{t-1}(x)+ h_t(x))$的基础上，加入正则项$\Omega(h_t) = \gamma J + \frac{\lambda}{2}\sum\limits_{j=1}^Jw_{tj}^2$其中，J是叶子节点的个数，$w_{tj}$是第j个叶子节点的最优值，这里的$w_{tj}$和GBDT中的$c_{tj}$是一个意思，Xgboost论文中用的是w表示叶子的值，这里和论文保持一致。

损失函数的二阶展开：

$\begin{align} L_t & = \sum\limits_{i=1}^mL(y_i, f_{t-1}(x_i)+ h_t(x_i)) + \gamma J + \frac{\lambda}{2}\sum\limits_{j=1}^Jw_{tj}^2 \\ & \approx \sum\limits_{i=1}^m( L(y_i, f_{t-1}(x_i)) + \frac{\partial L(y_i, f_{t-1}(x_i) }{\partial f_{t-1}(x_i)}h_t(x_i) + \frac{1}{2}\frac{\partial^2 L(y_i, f_{t-1}(x_i) }{\partial f_{t-1}^2(x_i)} h_t^2(x_i)) + \gamma J + \frac{\lambda}{2}\sum\limits_{j=1}^Jw_{tj}^2 \end{align}$

为了方便，记第i个样本在第t个弱学习器的一阶和二阶导数分别为：

$g_{ti} = \frac{\partial L(y_i, f_{t-1}(x_i) }{\partial f_{t-1}(x_i)}, \; h_{ti} = \frac{\partial^2 L(y_i, f_{t-1}(x_i) }{\partial f_{t-1}^2(x_i)}$

则损失函数可以表达为：

$L_t \approx \sum\limits_{i=1}^m( L(y_i, f_{t-1}(x_i)) + g_{ti}h_t(x_i) + \frac{1}{2} h_{ti} h_t^2(x_i)) + \gamma J + \frac{\lambda}{2}\sum\limits_{j=1}^Jw_{tj}^2$

第一项是常数，对最小化loss无影响，可以去掉，同时由于每个决策树的第j个叶子节点的取值最终是同一个值$w_{tj}$，因此损失函数简化为：

$\begin{align} L_t & \approx \sum\limits_{i=1}^m g_{ti}h_t(x_i) + \frac{1}{2} h_{ti} h_t^2(x_i)) + \gamma J + \frac{\lambda}{2}\sum\limits_{j=1}^Jw_{tj}^2 \\ & = \sum\limits_{j=1}^J (\sum\limits_{x_i \in R_{tj}}g_{ti}w_{tj} + \frac{1}{2} \sum\limits_{x_i \in R_{tj}}h_{ti} w_{tj}^2) + \gamma J + \frac{\lambda}{2}\sum\limits_{j=1}^Jw_{tj}^2 \\ & = \sum\limits_{j=1}^J [(\sum\limits_{x_i \in R_{tj}}g_{ti})w_{tj} + \frac{1}{2}( \sum\limits_{x_i \in R_{tj}}h_{ti}+ \lambda) w_{tj}^2] + \gamma J \end{align}$

把每个叶子节点区域样本的一阶和二阶导数的和单独表示如下：

$G_{tj} = \sum\limits_{x_i \in R_{tj}}g_{ti},\; H_{tj} = \sum\limits_{x_i \in R_{tj}}h_{ti}$

最终损失函数的形式可以表示为：

$L_t = \sum\limits_{j=1}^J [G_{tj}w_{tj} + \frac{1}{2}(H_{tj}+\lambda)w_{tj}^2] + \gamma J$

 

问题1：xgboost如何使用MAE或MAPE作为目标函数？参考链接

xgboost需要目标函数的二阶导数信息（或者hess矩阵），在回归问题中经常将MAE或MAPE作为目标函数，然而，这两个目标函数二阶导数不存在。

$MAE=\frac{1}{n}\sum_1^n|y_i-\hat y_i|$，$MAPE=\frac{1}{n}\sum _i^n \frac{|y_i-\hat y_i|}{y_i}$

其中，$y_i$是真实值，$\hat y_i$是预测值

方法（1）：利用可导的函数逼近MAE或MAPE---MSE、Huber loss、Pseudo-Huber loss

　　利用MSE逼近是可以的，但是MSE在训练初误差较大的时候，loss是其平方，会使得训练偏离MAE的目标函数，一般难以达到高精度的要求。

　　利用Huber loss进行逼近也可以，但是Huber loss是分段函数，不方便计算，其中$\delta$是可调节参数。

　　

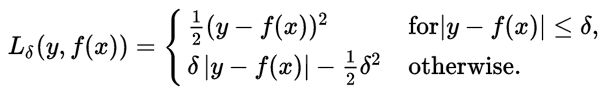
　　实际采用Huber loss的可导逼近形式：Pse