LGV 引理

LGV 引理（Lindstrom-Gessel-Viennot lemma）

本文主要分为对 引理的阐述与证明 和 这道题的解法。然鹅OIer 不需要证明。

LGV 引理 内容

• GG 是一个有限的带权有向无环图。每个顶点的度是有限的，不存在有向环（所以路径数量是有限的）。
• 起点 A={a1,⋯ ,an}A={a1​,⋯,an​}，终点 B={b1,⋯ ,bn}B={b1​,⋯,bn​}。
• 每条边 ee 有权 wewe​，并假定值属于某 交换环 。
• 对于一个有向路径 PP，定义 ω(P)ω(P) 为路径上所有边权的积。
• 对任意顶点 aa，bb，定义 e(a,b)=∑P:a→bω(P)e(a,b)=P:a→b∑​ω(P)。

设矩阵

M=(e(a1,b1)e(a1,b2)⋯e(a1,bn)e(a2,b1)e(a2,b2)⋯e(a2,bn)⋮⋮⋱⋮e(an,b1)e(an,b2)⋯e(an,bn))M=⎝⎜⎜⎜⎜⎛​e(a1​,b1​)e(a2​,b1​)⋮e(an​,b1​)​e(a1​,b2​)e(a2​,b2​)⋮e(an​,b2​)​⋯⋯⋱⋯​e(a1​,bn​)e(a2​,bn​)⋮e(an​,bn​)​⎠⎟⎟⎟⎟⎞​

从 AA 到 BB 的不相交路径 P=(P1,P2,⋯ ,Pn)P=(P1​,P2​,⋯,Pn​)，PiPi​ 表示从 aiai​ 到 bσ(i)bσ(i)​ 的一条路径，其中 σσ 是一个排列（置换），并且满足对任意 i≠ji=j，PiPi​ 与 PjPj​ 没有公共点。记 σ(P)σ(P) 表示 PP 对应的排列。

引理说明，MM 的行列式是所有从 AA 到 BB 的不相交路径 P=(P1,⋯ ,Pn)P=(P1​,⋯,Pn​) 的带符号和。其中符号指 σ(P)σ(P) 的逆序数的奇偶性： (−1)逆序数(−1)逆序数，记为 sign(σ(P))sign(σ(P))。

det(M)=∑P:A→Bsign(σ(P))∏i=1nω(Pi)det(M)=P:A→B∑​sign(σ(P))i=1∏n​ω(Pi​)

证明

对一组路径 PP，若对任意 i≠ji=j，PiPi​ 与 PjPj​ 无公共点，则称 PP 是一组不相交路径，否则为一组相交路径。为了简便，在下面相交路径记作 PcPc，不相交路径记作 PuPu。不做特殊说明时，PP 为一组平凡的路径。当带下标时，指一条路径。定义 ω(P)=ω(P1)ω(P2)⋯ω(Pn)ω(P)=ω(P1​)ω(P2​)⋯ω(Pn​)。

根据定义，

det(M)=∑σ∈Snsign(σ)∏i=1ne(ai,bσ(i))=∑σ∈Snsign(σ)∏i=1n∑Pi:ai→bσ(i)ω(Pi)det(M)​=σ∈Sn​∑​sign(σ)i=1∏n​e(ai​,bσ(i)​)=σ∈Sn​∑​sign(σ)i=1∏n​Pi​:ai​→bσ(i)​∑​ω(Pi​)​

∏i=1n∑Pi:ai→bσ(i)ω(Pi)∏i=1n​∑Pi​:ai​→bσ(i)​​ω(Pi​) 展开后对应所有排列为 σσ 的路径组 PP ，

det(M)=∑σ∈Snsign(σ)∑Pω(P),P:(a1,⋯ ,an)→(bσ(1),⋯ ,bσ(n))=∑P:A→Bsign(σ(P))ω(P)det(M)​=σ∈Sn​∑​sign(σ)P∑​ω(P),P:(a1​,⋯,an​)→(bσ(1)​,⋯,bσ(n)​)=P:A→B∑​sign(σ(P))ω(P)​

现在等式的形式已与定理相像，但是 PP 的含义不同。

det(M)=∑Pu:A→Bsign(σ(Pu))ω(Pu)+∑Pc:A→Bsign(σ(Pc))ω(Pc)det(M)=Pu:A→B∑​sign(σ(Pu))ω(Pu)+Pc:A→B∑​sign(σ(Pc))ω(Pc)

故若引理成立，必有 ∑Pc:A→Bsign(σ(Pc))ω(Pc)=0∑Pc:A→B​sign(σ(Pc))ω(Pc)=0 。

设 CC 为所有 PcPc 构成的集合。如果我们能构造一个双射关系 f:C→Cf:C→C，满足对任意 Pc∈CPc∈C， ω(f(Pc))=ω(Pc)ω(f(Pc))=ω(Pc)，sign(σ(f(Pc)))=−sign(σ(Pc))sign(σ(f(Pc)))=−sign(σ(Pc))，根据重排列定理，

∑Pcsign(σ(Pc))ω(Pc)=∑Pcsign(σ(f(Pc)))ω(f(Pc))Pc∑​sign(σ(Pc))ω(Pc)=Pc∑​sign(σ(f(Pc)))ω(f(Pc))

∑Pcsign(σ(Pc))ω(Pc)=12∑Pcsign(σ(Pc))ω(Pc)+12∑Pcsign(σ(f(Pc)))ω(f(Pc))=12∑Pcsign(σ(Pc))ω(Pc)+12∑Pc−sign(σ(Pc))ω(Pc)=0Pc∑​sign(σ(Pc))ω(Pc)​=21​Pc∑​sign(σ(Pc))ω(Pc)+21​Pc∑​sign(σ(f(Pc)))ω(f(Pc))=21​Pc∑​sign(σ(Pc))ω(Pc)+21​Pc∑​−sign(σ(Pc))ω(Pc)=0​

确实可以构造：

考虑 P=(P1,P2,⋯ ,Pn)P=(P1​,P2​,⋯,Pn​)，P∈CP∈C，中找到最小的二元组 (i,j)(i,j) 满足 PiPi​ 和 PjPj​ 有交，将相交之后的路径交换一下，交换后得到 P′P′ 。显然有 P′∈CP′∈C，P′≠PP′=P。

 

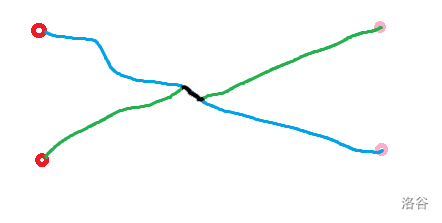
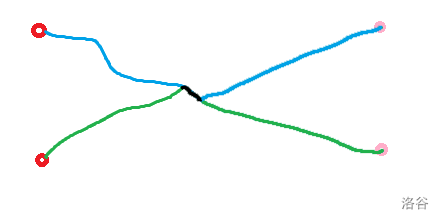
这里就不写式子了 可以直观理解一下 就是因为懒，因为边还是那些边，边权属于交换环，所以 ω(P)ω(P) 不变。另一个影响是交换了两条路径的终止节点，即交换了排列中的两个元素，根据我们学前班就学过的线性代数，逆序对数的奇偶改变，所以 sign(σ(P′))=−sign(σ(P))sign(σ(P′))=−sign(σ(P))。

最后我们还可以注意到，对于 P′P′，最小的二元组还应该是 (i,j)(i,j)，那么 f(P′)=Pf(P′)=P。籍此可证 ff 是双射。

证毕。