版权声明:本文为博主原创文章,未经博主允许不得转载。
本文是针对博主使用粒子群优化算法解决水面无人艇静态、动态障碍物规避,及场地布局三类问题,做了更深入的总结分析。
与目前火热的机器学习不同,智能优化算法需要对问题建立确定的模型,具有明确的优化目标函数,对优化变量不断的寻优。通过对三种算法的问题描述、模型建立、算法参数确定、算法流程描述、计算结果分析,及从维度、优化变量、优化目标、针对业务的PSO优化四个方面,对应用在不同场景下的三种粒子群算法进行对比总结,旨在更彻底的剖析如何将粒子群优化算法应用到具体的问题中。
本文的形式是按照《粒子群算法实战分享PPT》结构,对每页PPT内容进行阐述。
博主分享的PPT是原版包含动画的PPT(Office版本越高越好,至少2010,否则有些动画在低版本显示有问题),自我感觉PPT做的很正、很文艺范,是博主7年来打杂做各种PPT经验的大成之作(说白了也就这水平),相信看完原版PPT你就会觉得原来技术分享也可以这么文艺范!
下载地址:《粒子群算法实战分享 - CSDN博主dkjkls》。
参考文章:
1. 《水面无人艇局部危险避障算法研究 第1章 绪论》
2. 《第3章 基于PSO的已知静态路径规划方法》
3. 《第4章 基于PSO并融合海事规则的已知动态路径规划方法》
4. 粒子群优化算法解决场地资源布局问题-算法原型探讨
目录
本文将首先介绍下粒子群优化算法,简述PSO发现过程,通过二维动画示例形象生动的描绘PSO的寻优过程,解释PSO迭代公式、计算流程,并给出C++实现的PSO基本框架。
第2节将结合博主在硕士毕业论文中使用PSO优化的两种场景,分别从算法背景介绍、建模、粒子群参数选择、算法流程、仿真分析着手,分析如何通过PSO解决无人艇避障中两种不同的问题。
第3节将结合博主使用PSO解决的另外一个实际问题 - 场地布局,简要介绍场地布局问题描述、粒子群参数选择、算法流程,并对计算结果和优势进行分析,最后指出该算法的不足及仍需探讨的问题。
第4节将从维度、优化变量、优化目标、针对业务的PSO优化四个方面,对应用在不同场景下的三种粒子群算法进行对比,并进行总结。
1 粒子群算法介绍
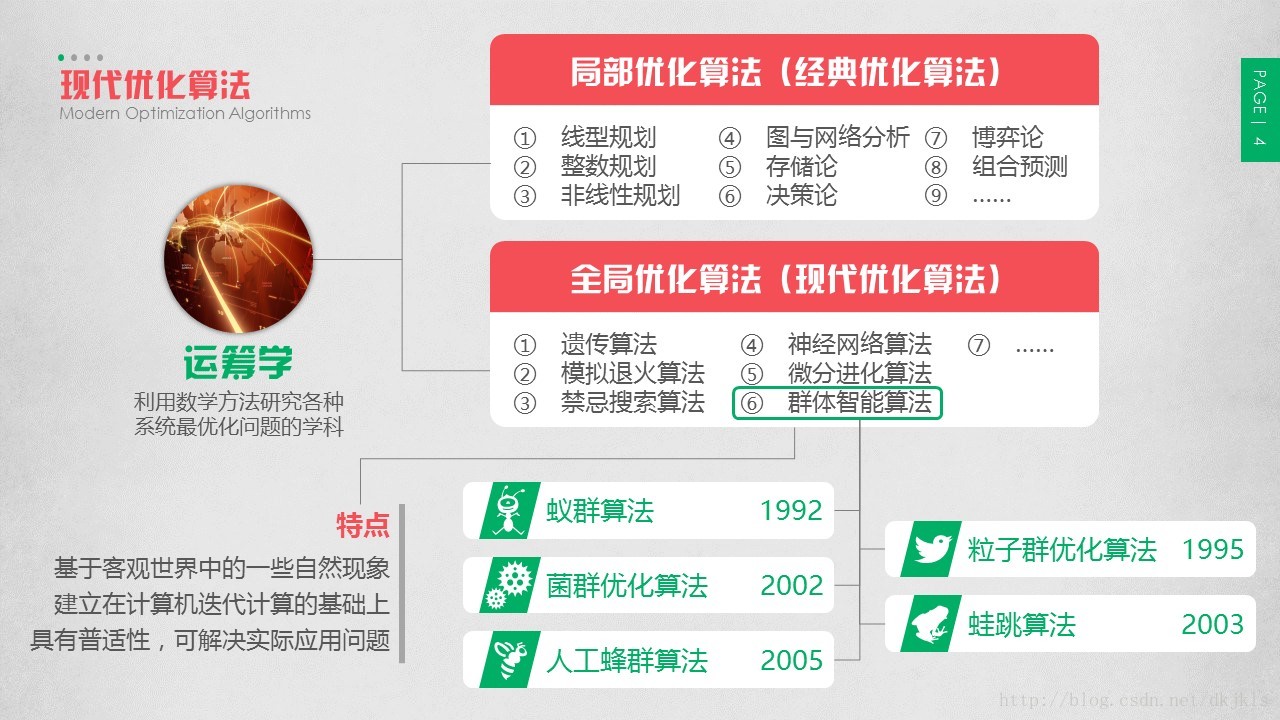
1.1 现代优化算法
运筹学是现代管理学的一门重要专业基础课。它是20世纪30年代初发展起来的一门新兴学科,其主要目的是在决策时为管理人员提供科学依据,是实现有效管理、正确决策和现代化管理的重要方法之一。该学科是应用数学和形式科学的跨领域研究,利用统计学、数学模型和算法等方法,去寻找复杂问题中的最佳或近似最佳的解答。运筹学经常用于解决现实生活中的复杂问题,特别是改善或优化现有系统的效率。 研究运筹学的基础知识包括实分析、矩阵论、随机过程、离散数学和算法基础等。而在应用方面,多与仓储、物流、算法等领域相关。因此运筹学与应用数学、工业工程、计算机科学、经济管理等专业密切相关。
运筹学是一种科学决策的方法
运筹学是依据给定目标和条件从众多方案中选择最优方案的最优化技术
运筹学是一种给出坏的问题的答案的艺术,否则的话问题的结果会更坏
习惯上,将优化算法分为两类:局部优化算法和全局性优化算法。
前者可以称为经典优化算法,己经得到了人们广泛深入的研究。目前,运筹学(确定论方法)主要包括这些方面的内容,线性规划、整数规划、0一1规划、非线性规划、排队论、决策论。后者习惯上称为现代优化算法,是20世纪80年代兴起的新型全局性优化算法,主要包括禁忌搜索、模拟退火、遗传算法等,其主要应用对象是优化问题中的难解问题,即NP-hard问题。
经典优化算法的局限:
解法是特定的:不同的问题需要使用不同的解法;
所能解决的问题是有限的:和数学工具直接相关,若没有解决问题的数学方法,则难以解决。
现代优化算法
现代优化算法又称智能优化算法或现代启发式算法,是一种具有全局优化性能、通用性强、且适合于并行处理的算法。这种算法一般具有严密的理论依据,而不是单纯凭借专家经验,理论上可以在一定的时间内找到最优解或近似最优解。
特点:从任一解出发,按照某种机制,以一定的概率在整个求解空间中探索最优解。由于它们可以把搜索空间扩展到整个问题空间,因而具有全局优化性能。
1.2 粒子群优化算法
粒子群优化算法(PSO)最初是由Kennedy和Eberhart博士于1995年受人工生命研究的结果启发,在模拟鸟群觅食过程中的迁徙和群集行为时提出的一种基于群体智能的演化计算技术。
PSO算法起源于对飞行鸟群觅食行为的研究。在鸟群捕食的时候,当有一只鸟发现不远处的食物后,它将飞向食物地点,这将导致它周围的其它鸟也沿着这个方向寻找食物地点,直到整个鸟群全部降落在此,找到食物。这是一种自然状态下的信息共享机制,在认知和搜寻过程中,个体会记住自身的飞行经验;同时,也向其它优秀个体学习,当它发现其它的某个个体飞行更好的时候,就会向它学习并对自身做出适当的调整,使得自己能朝着更好的方向飞行。
该算法具有并行处理、鲁棒性好等特点,能以较大概率找到问题的全局最优解,且计算效率比传统随机方法高。其最大的优势在于编程简单,易实现、收敛速度快,而且有深刻的智能背景,既适合科学研究,又适合工程应用。因此,PSO一经提出,立刻引起了演化计算领域研究者的广泛关注,并在短短几年时间里涌现出大量的研究成果,该算法目前已被“国际演化计算会议”列为讨论专题之一。
PSO是受到鸟群或者鱼群社会行为的启发而形成的一种基于种群的随机优化技术。它是一类随机全局优化技术,通过粒子间的相互作用发现复杂搜索空间中的最优区域。该算法是一种基于群体智能的新型演化计算技术,具有简单易实现、设置参数少、全局优化能力强等优点。粒子群优化算法已在函数优化、神经网络设计、分类、模式识别、信号处理、机器人技术等许多领域取得了成功的应用。
PSO优缺点:
PSO算法是一种启发式的优化计算方法,其最大的优点:
⑴易于描述,易于理解;
⑵对优化问题定义的连续性无特殊要求;
⑶只有非常少的参数需要调整;
⑷算法实现简单,速度快;
⑸相对其它演化算法而言,只需要较小的演化群体;
⑹算法易于收敛,相比其它演化算法,只需要较少的评价 函数计算次 数就可达到收敛;
⑺无集中控制约束,不会因个体的故障影响整个问题的求解,确保了系统具备很强的鲁棒性。
PSO的缺点:
对于有多个局部极值点的函数,容易陷入到局部极值点中,得不到正确的结果。此外,由于缺乏精密搜索方法的配合,PSO方法往往不能得到精确的结果。再则,PSO方法提供了全局搜索的可能,但并不能严格证明它在全局最优点上的收敛性。因此,PSO一般适用于一类高维的、存在多个局部极值点而并不需要得到很高精度的优化问题。
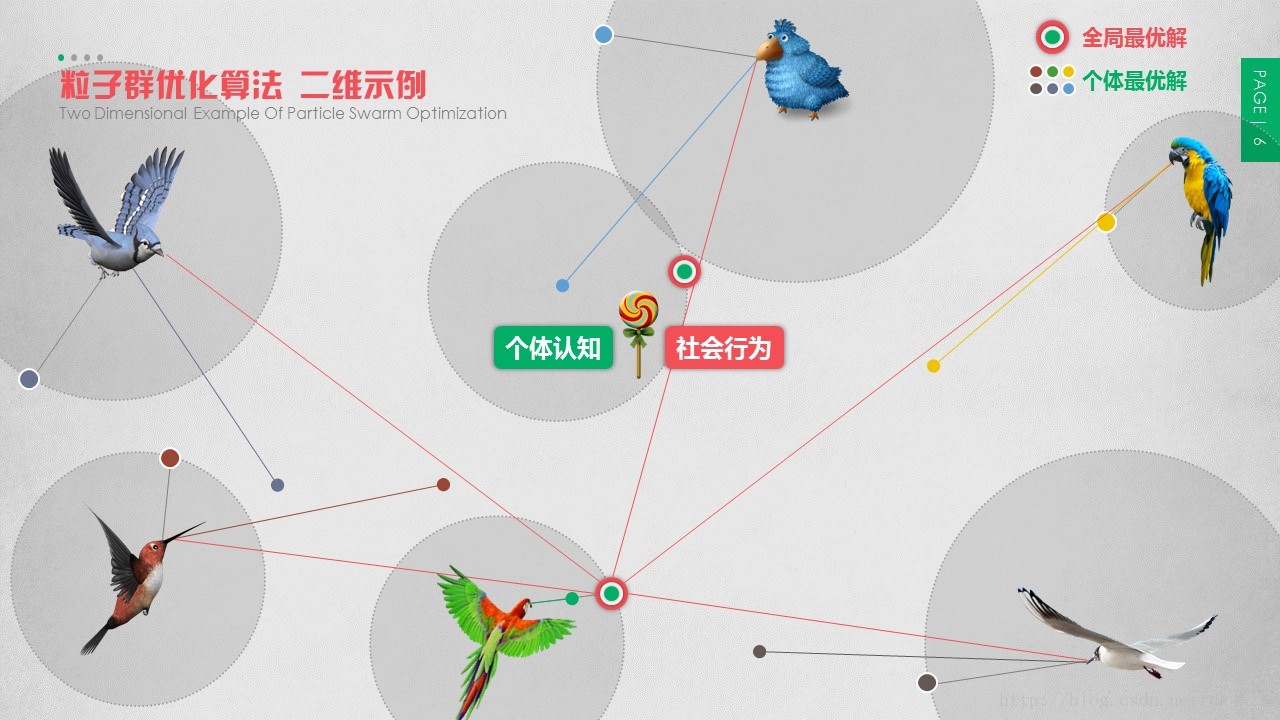
1.3 粒子群优化算法 二维示例
假设这样一个场景:一群鸟(6只,即PSO粒子数为6)随机的分布在二维空间区域中,在这个区域只有一个食物(棒棒糖),每只鸟都想吃到这个棒棒糖。所有的鸟都不知道食物具体位置在哪里,但他们知道他们各自当前位置与食物的距离。在飞行了几次(迭代次数)后,每只鸟都能从自己的几次飞行经验中得到自己距离棒棒糖最佳的位置,即个体认知行为。若每只鸟朝着自己飞行过的最佳位置前进的同时,追寻所有鸟中目前离食物最近的位置(即鸟群的社会行为),即可发挥群体觅食优势,更快的找到食物。如果把食物当作最优点,而把鸟离食物的距离当作函数的适应度,那么鸟寻觅食物的过程就可以当作一个函数寻优的过程。由此受到启发,经过简化提出了粒子群优化算法。
1.4 粒子群优化算法 迭代公式
粒子群优化算法迭代公式,包括速度和位置公式。
从速度迭代公式可知,粒子的下一代速度与自己本代速度的惯性、个体最优解、全局最优解有关。
1.5 粒子群优化算法 流程及实现
粒子群算法的基本框架还算是比较简单的,算法框架示例是C++实现的。
2 无人艇避障算法
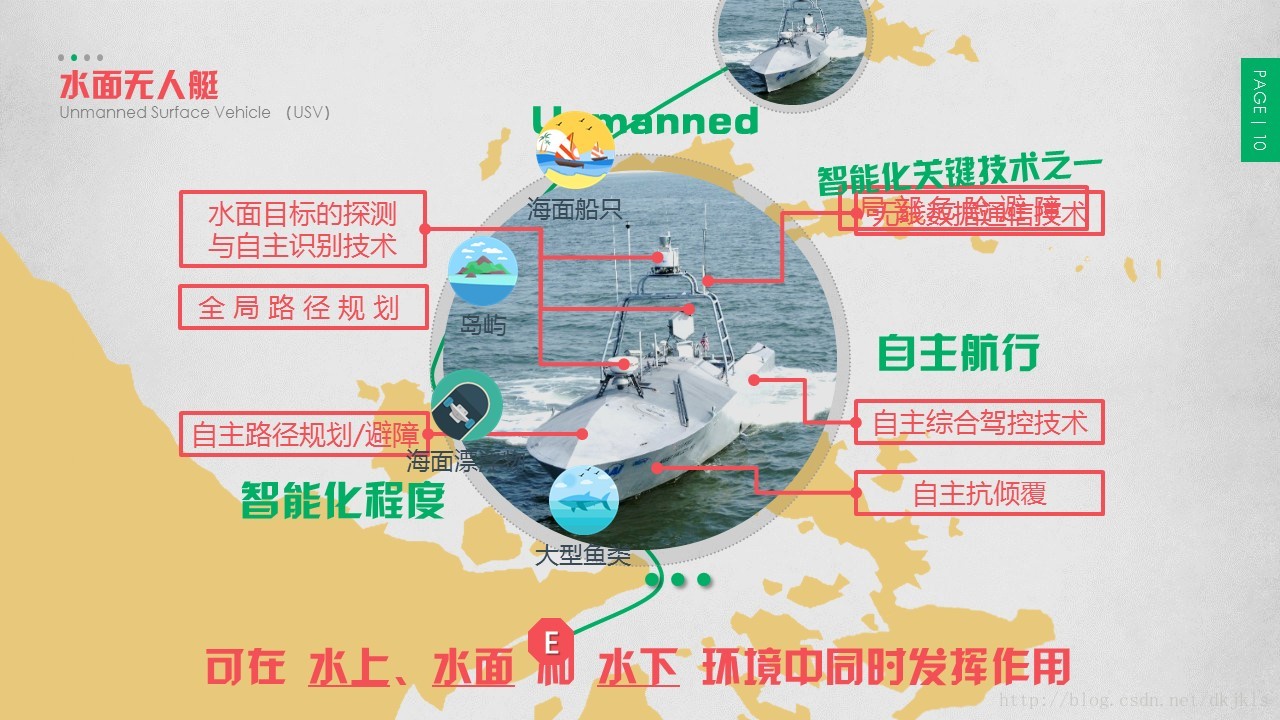
2.1 水面无人艇
水面无人艇(USV,Unmanned Surface Vehicle)属于自主式海洋运载器,其优势是在不适合载人船艇或者危险情况下执行任务。相比于无人机、地面机器人和水下机器人等,水面无人艇的发展起步较晚,但是随着海洋地位的提高,其发展势头强劲。目前,水面无人艇在军事、民用领域的应用也频频见诸报端。相比于其它无人驾驶运载工具,只有水面无人艇(USV)可以在水上、水面和水下环境中同时发挥作用;且无人艇具有智能化、模块化、体积小、无人、高速、机动灵活、适应各种气候环境、性价比高等优势,不难看出海面无人艇将在海洋的探索和开发利用中,以及在未来可能的海上冲突等军事的应用中起到不可忽视的作用。
在水面无人艇的研究和应用课题中,智能化将是其发展的一个重要方向。水面无人艇的智能化关键技术主要体现在:自主综合驾控技术、水面目标的探测与自主识别技术、自主导航技术、智能规划与决策技术等方面。而我国在这方面仍处于起步阶段,很多技术还相当薄弱,与美国等发达国家相比,存在巨大的差距。虽然我们在USV方面的研究起步较晚,但已经越来越受到人们的重视,国内也有很多学者开始研究USV的相关技术。
本节的无人艇避障算法,是在全局路径规划基础上进行的,在无人艇沿全局路径规划算法规划出来的航行航行过程中,难免会遇到静态或动态障碍物,若要无人艇安全抵达目的地,必须对这些障碍物进行避障。
2.2 水面无人艇 分布
水面无人艇技术的发展可以追溯到第二次世界大战,首次尝试是设计成鱼雷形状清除沿海区域的地雷和障碍物;1946年,在基尼环礁进行核试验后,无人艇被用来收集该地的放射性水样;另一个常见用法是(现在仍然是)使用无人艇作为目标靶船进行训练。目前,水面无人艇在民用、军事上的成功应用都展现了其广阔的前景,世界上诸多发达国家也都在其相关技术的研究中投入了大量的金钱和精力。其中,美国和以色列开始较早,相关的技术更加成熟;其它发达国家如德国、英国、法国、日本等国,在无人艇研制方面已经取得了很大的进展,并已经有相当多的研究成果得到了实际的应用。
详见《水面无人艇局部危险避障算法研究 第1章 绪论》。
2.3 水面无人艇局部危险避障
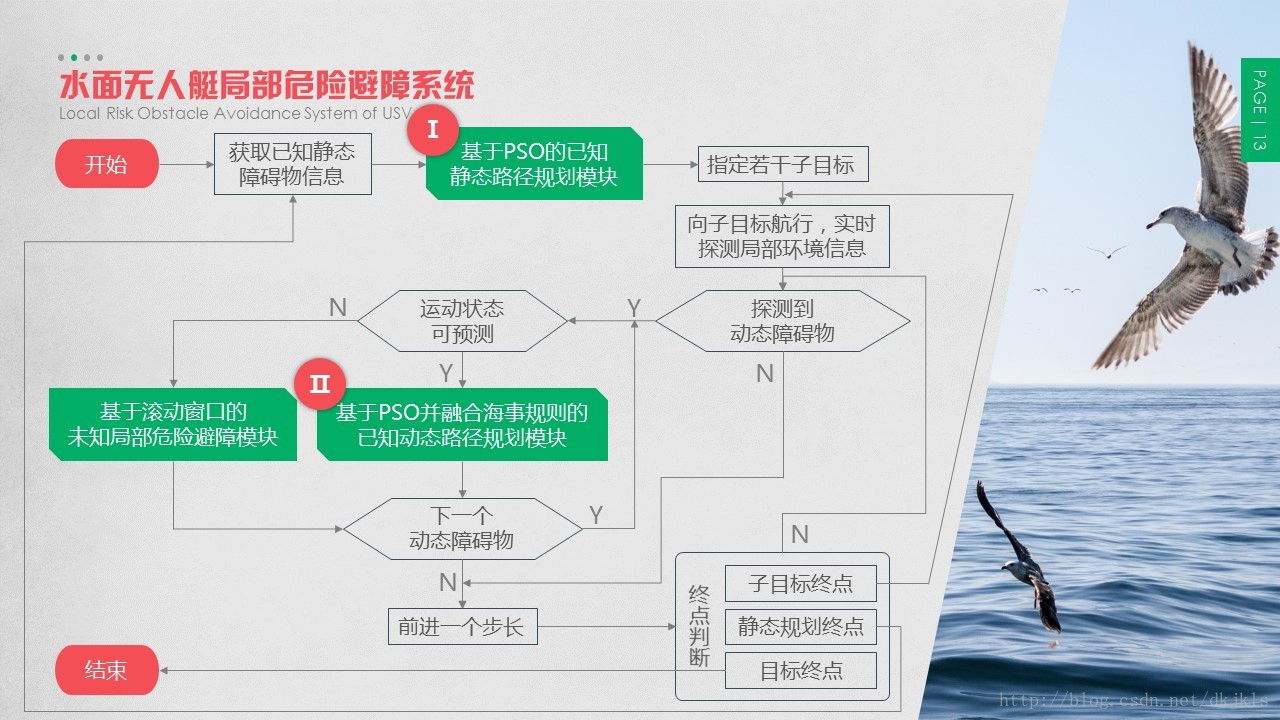
2.4 水面无人艇局部危险避障系统
Ⅰ基于PSO的已知静态路径规划模块,Ⅱ基于PSO并融合海事规则的已知动态路径规划模块,即为水面无人艇局部危险避障系统的第一二层算法,也是本文讲解的两种算法。
2.5 基于PSO的已知静态路径规划方法
无人艇在航行中,需对通过雷达或AIS(Automatic Identification System,船舶自动识别系统)探测到的静态障碍物进行躲避,即本节提出的基于PSO的已知静态路径规划方法。
详见《第3章 基于PSO的已知静态路径规划方法》。
2.5.1 无人艇已知静态路径规划
2.5.2 极坐标系下的建模
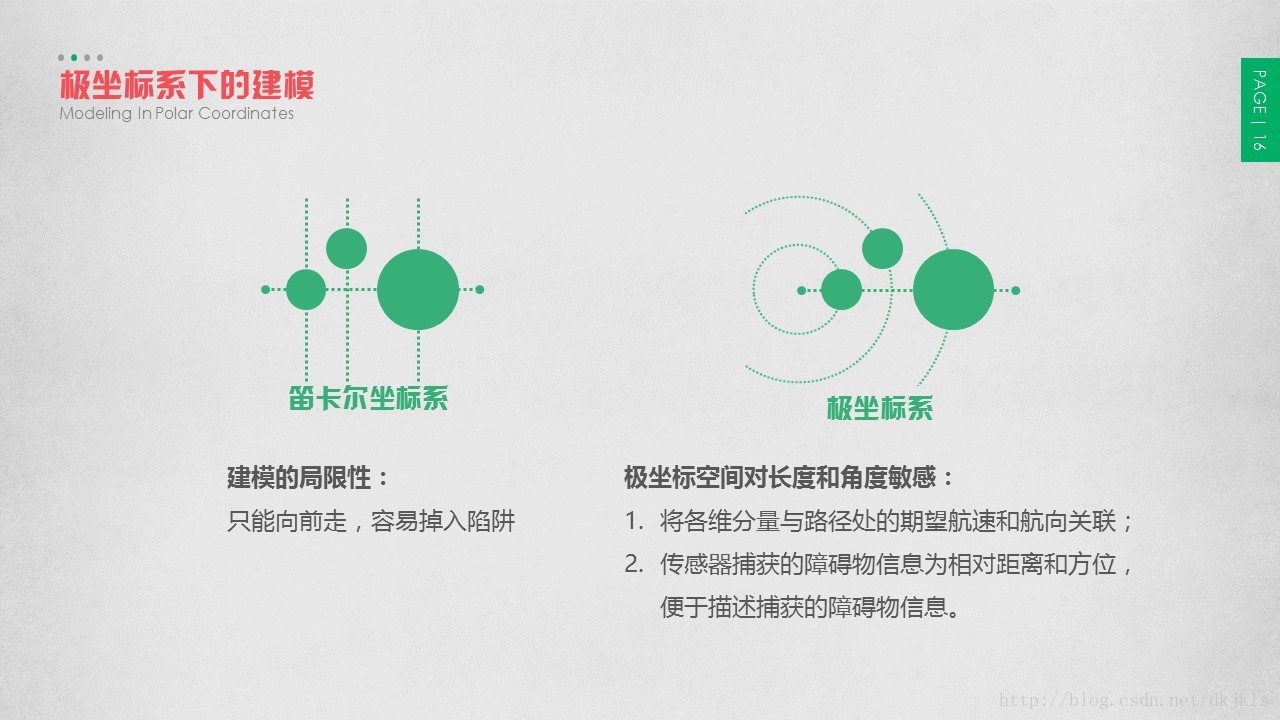
对于水面无人艇来说,基于环境先验知识的已知局部危险避障是一种在线路径规划策略,不仅要求路径最优,最重要的还需要满足较少的规划时间,即保证路径规划的时效性。
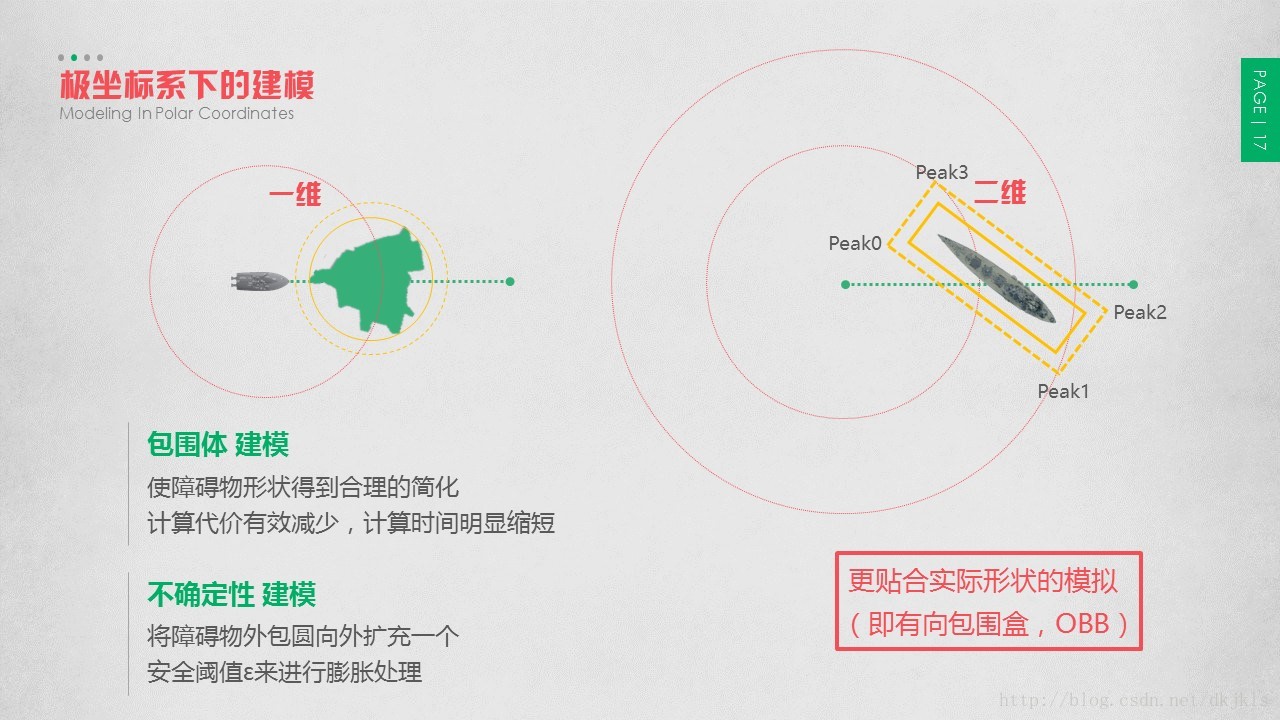
然而对于真实环境下,障碍物的形状各种各样,通过雷达扫描出来的雷达图像或通过声呐、传感器得到的障碍物形状可能会很复杂,直接对这些未经处理的障碍物形状进行避障,其计算过程往往会代价高昂,导致计算时间增加。为了减少计算消耗,缩短计算时间,在进行路径规划之前,需要对障碍物进行包围体处理,使障碍物形状得到合理的简化。
本文对障碍物的包围体处理包括两种方式:对于长宽比较小的障碍物用圆形进行包围,而对于长宽比较大的障碍物用有向包围盒(OBB,即具有方向性的矩形)进行包围。下面分别就两种障碍物处理方式进行说明。
无人艇在海面航行过程中,会存在许多不确定性因素,如障碍物运动的不确定性、无人艇本身运动的不确定性、执行机构存在计算时的误差、执行机构运行时的不确定性、无人艇自身定位和对障碍物进行探测的系统也不可避免的存在误差、不可避免地存在精度、误差、漂移等。由于存在诸多不确定性因素,且在本文的计算中,为了简化计算,将水面无人艇作为一个质心处理,所以需要对障碍物进行膨胀建模。对于障碍物的不确定性建模,本文将障碍物外包圆向外扩充一个安全阈值ε(本文取五倍船长)来进行膨胀处理。
极坐标系的建立如图所示。
其中“Start”代表起始点,“Goal”代表目标点。起始点和目标点的连线即为极坐标系的坐标轴,起始点Start为极点,逆时针方向为正。
对于基于PSO的已知静态路径规划中,需要确定记录路径节点信息的维度圆如图中的橙色虚线。维度圆为以极点即起始点为圆心,每个障碍物的维度点的极径值为半径,得到的一组同心圆。外包圆的维度点为外包圆的圆心,有向包围盒的维度点有两点,分别为四个顶点中极径值位于中间的两点。至此,就得到了一组同心圆,每一个同心圆都代表了粒子群中的一个维度,同心圆越多,环境越复杂。该图就是一个集已知、未知静动态障碍物并存的极坐标系下的环境建模图,其中包括3个已知静态圆形障碍物(SOC1,SOC2,SOC3),3个已知静态矩形障碍物(SOR1,SOR2,SOR3),2个已知动态圆形障碍物(DOC1,DOC2),1个已知动态矩形障碍物(DOR1),1个未知动态圆形障碍物(UOC1),1个未知动态矩形障碍物(UOR1)。
2.5.3 PSO路径优化算法参数确定
粒子群优化算法是通过适应度函数值来确定粒子的好坏的,是引导PSO向最优解逼近的决定性因素。可以说适应度函数选择的好坏,将直接影响算法的性能。
本文要求的性能指标,为一条长度最短的可行路径,且不能与障碍物相交。所以本文以路径长度值作为适应度函数值。
对于上面所说的适应度函数而言,取值越小说明粒子越优秀。适应度函数分为两个部分:可行避障路径与不可行避障路径。可行路径的适应度函数值即为最优路径的长度,不可行路径的适应度函数值设为无穷大。
2.5.4 路径可行性的判断
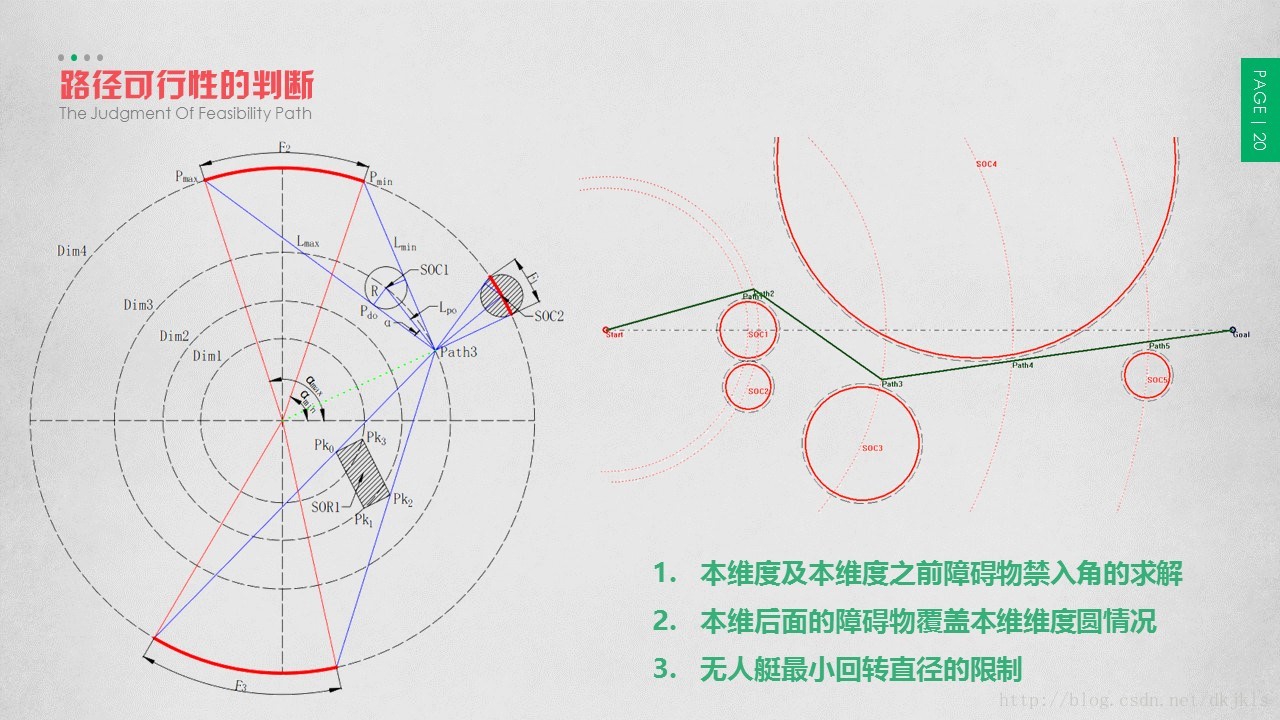
采用PSO进行路径规划过程中,假设已经计算到了第i维的路径点,下一步需要计算第i+1维上的路径点;此时PSO路径优化算法需要判断在第i+1维上有哪些圆弧段,是由于该维之前的障碍物阻碍导致不能进入的,而这些不能进入的圆弧段称之为该维的禁入域。
如图1所示,该状态为路径优化算法已经计算到了Path3这一点,下一步需要计算Dim4上的路径节点,图中共有F1、F2、F3三段禁入域,其中F1、F2分别为SOC2和SOC1产生的禁入域,F3为SOR1产生的禁入域。为了使计算更加快捷,本文采用动态计算禁入域,即计算到某一维的路径点时,只需计算该维之前障碍物所产生的禁入域,而该维后面的障碍物在本维中无需计算,从而节省了大量的计算量,缩短了计算时间。
2.本文算法进行禁入域计算时,只计算了该维之前障碍物所产生的禁入域,还有一种情况需要进行考虑:后面的障碍物因过大或与上一维距离较近的情况下,覆盖了本维的维度圆,如图2中的SOC2覆盖了SOC1的维度圆,SOC4覆盖了SOC3的维度圆。对于这种情况需要确保路径点不能在障碍物扩展的圆或矩形中,所以在进行完禁入角的判断后,还需要对这种情况进行判断。
3.无人艇最小回转直径的限制。
无人艇不能像陆上机器人那样可以快速的转向或改变速度,无人艇要改变其运动状态,需要一定的反应时间,并符合无人艇的最小回转直径的要求。所以对产生的路径节点,先根据无人艇当时运动的速度确定最小回转直径,再根据前后路径段的方向确定该节点最小回转圆形的圆心和回转圆弧段。并对回转圆弧段与障碍物进行相交运算,若与障碍物相交则判为不可行解。
2.5.5 引入启发式知识的初始化路径
启发式知识是指用与实际问题相关的知识和经验来指导问题的求解,可很好的提高算法的搜索能力,以及加快算法的收敛速度。
基本的粒子群优化算法是在工作区中随机的产生关键点,对于在极坐标系下则是随机的产生(-π~π]之间的角度值。然而对于本文所设立的极坐标系而言(极轴方向即为起点至目标点方向),预期的最优极角无疑应是在0°左右徘徊;若随机产生极角,会产生很多不必要的搜索操作,降低PSO的搜索效率。考虑到上述因素,本文在粒子初始化(即生成路径点极角)时,加入正态分布赋值函数,以期初始化产生相对极轴较小的偏转角度Δαi。本文所设置的正态分布初始化赋值符合正态分布N(0,(π/2)2),并通过函数设置,只产生(-π~π]之间的角度值,Δαi赋值分布图如图所示。
加入正态分布初始化的粒子群路径规划算法,可使得初始化生成的路径上下颠簸幅度减少,同时可保证粒子群随机分布在较为合理的搜索空间中。
2.5.6 引入路径平滑优化处理的路径规划算法
对于本文采用PSO计算最优路径,若仅仅采用引入启发式知识的基本粒子群优化算法进行计算,会发现该方法在路径规划应用上的不足:
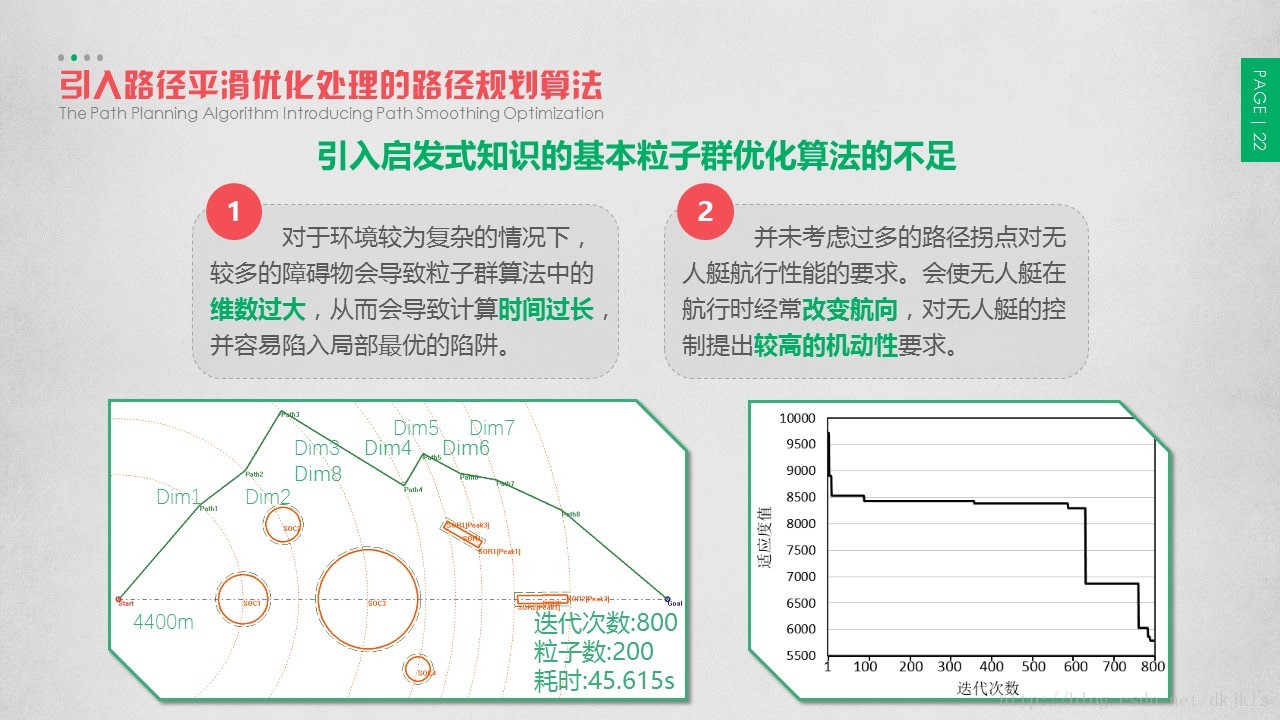
(1) 对于环境较为复杂的情况下,较多的障碍物会导致粒子群算法中的维数过大,从而会导致计算时间过长,并容易陷入局部最优的陷阱。
如图3-10中的情况所示,该环境下包括4个已知静态圆形障碍物和2个已知静态矩形障碍物,起始点和目标点之间的连线路径长度为4400m,每个粒子包括8个维度。设置粒子数为200,迭代次数为800,进行计算,图中路径即为引入启发式知识的基本粒子群优化算法解算出的最优路径,图为本次计算适应度值随迭代次数变化的情况。从图可以看出算法在8代时就已得到了不是最优的收敛,并陷入了局部最优的状态,一直到第794代才得到了相对可行的路径,但确是消耗计算时间为代价的,进行本次计算的耗时为45.615s,显然是很不合理的一组解算。
(2) 引入启发式知识的基本粒子群优化算法在计算时,并未考虑过多的路径拐点对无人艇航行性能的要求。若将规划出来的路径直接作为航行路径,无疑会使无人艇在航行时经常改变航向,不仅做了很多没有必要的运动,而且会对无人艇的控制提出较高的机动性要求。
如图中的情况所示,该环境为8个维度,在行进到每一个维度时都需要进行转向。
由于引入启发式知识的基本粒子群优化算法存在上述的不足,所以需要对该算法再引入路径平滑优化处理方法,使得算法得到最优解的耗时缩短、需转弯的次数最少。
本文采取的路径平滑优化处理方法为:
为了考虑全局最优性,从起始点开始与该点后面的路径点倒序相连,若该段连线不与障碍物相交,则选取这段连线为子路径段,并求出子路径段中间路径点的坐标值并赋予最优路径数组;直到求解到倒数第二个路径点为止。对于环境更为复杂的情况来说,进行一次路径平滑优化处理,还不足以得到最优的路径解,所以需要对优化后的路径多次进行优化,直到适应度函数值不再改变为止。
经过大量实验可以得出,采用加入路径平滑优化处理的PSO算法解算路径时,将PSO设置为粒子数100,迭代次数50,可以较好的平衡计算耗时和路径的最优解。
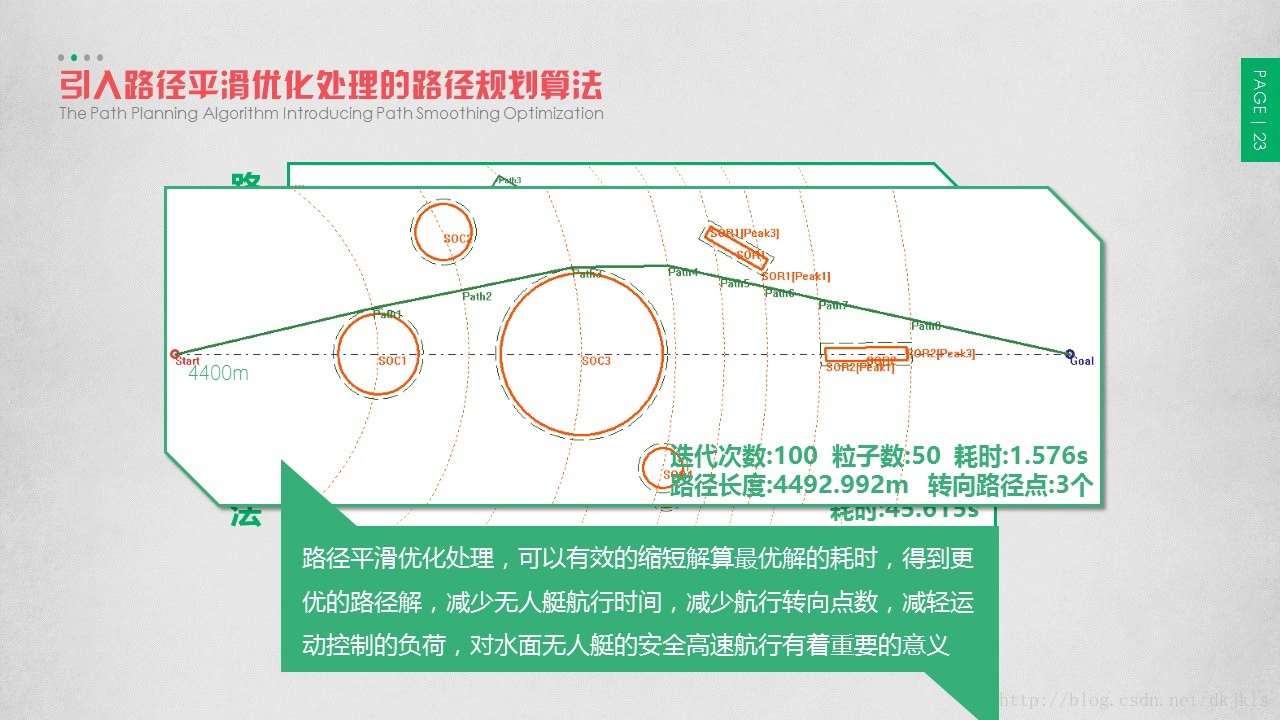
采用加入路径平滑优化处理的PSO算法对图所示的情况再次进行计算,得到的最优路径如图所示。该次计算所用耗时为1.576s,最优适应度函数值(即路径长度)为4492.992m;而所需转向的路径点为Path1、Path3、Path4这三处路径点,且从图上可以看出,每个转向点所需转向的角度都不大。
由此可以看出,对采用引入启发式知识的基本粒子群优化算法产生的路径的基础上,进行路径平滑优化处理,可以有效的缩短解算最优解的耗时,得到更优的路径解,减少无人艇航行时间,减少航行转向点数,减轻运动控制的负荷,对水面无人艇的安全高速航行有着重要的意义。
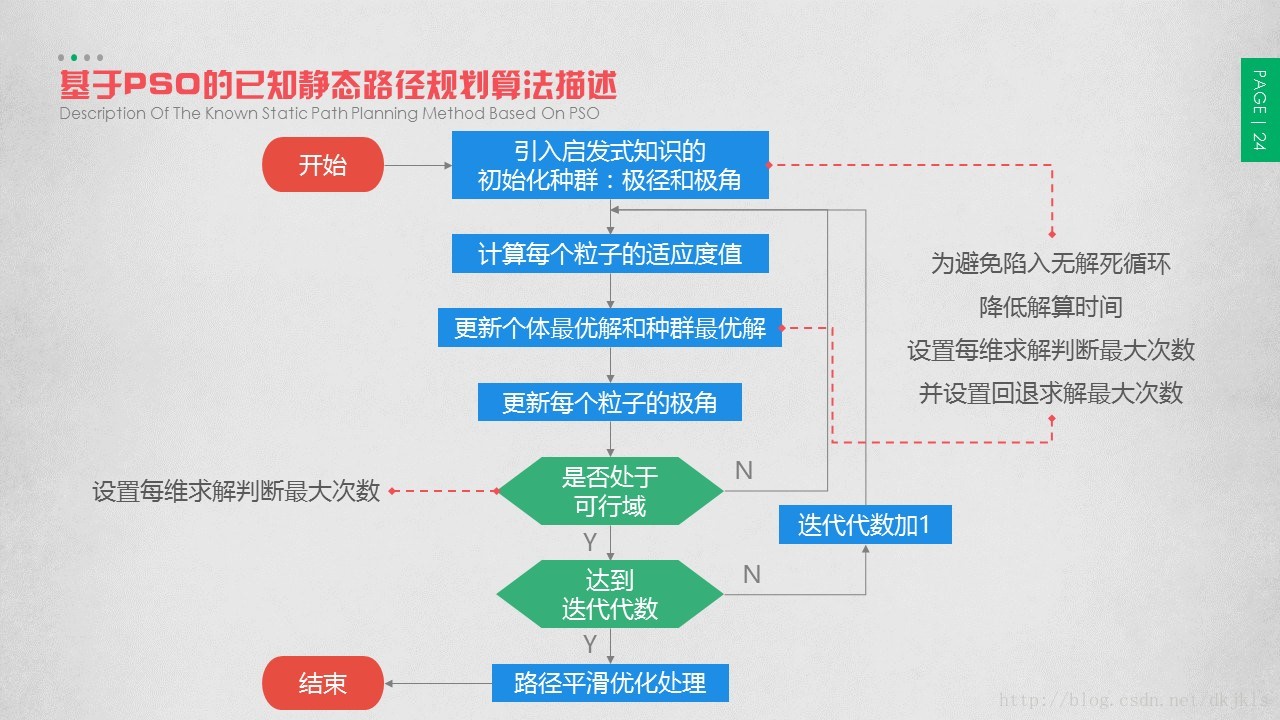
2.5.7 基于PSO的已知静态路径规划算法描述
需要说明的是,为达到降低解算时间,实时快速避障的目的,对粒子群优化算法中需要循环求解可行极角处,设定一个求解判断最大次数,若大于此值,就放弃此粒子在本代的解,以免陷入局部最优。在本算法中,需要设置求解最大次数的迭代处包括两个部分,下面分别来进行描述。
第一部分为“引入启发式知识的初始化种群”处,在该部分进行初始化时,需要设置每一维求解判断最大次数;若维数较大,在某一维处求解判断极角超过最大次数,此时需要退回上一维重新求解上一维的极角;同时需要设置进行此种回退方法的最大次数,超过最大次数则将该粒子作废。
第二部分为“是否处于可行域”处,该部分在更新粒子极角时,需要判断是否处在可行域,若不在可行域内,则继续求解。对此部分设置求解判断最大次数,若大于此值,就放弃此粒子在本代的解,该粒子的最佳适应度值设为之前代数所求解得到的最佳适应度值,以免陷入局部最优。
2.5.8 仿真实验结果及分析
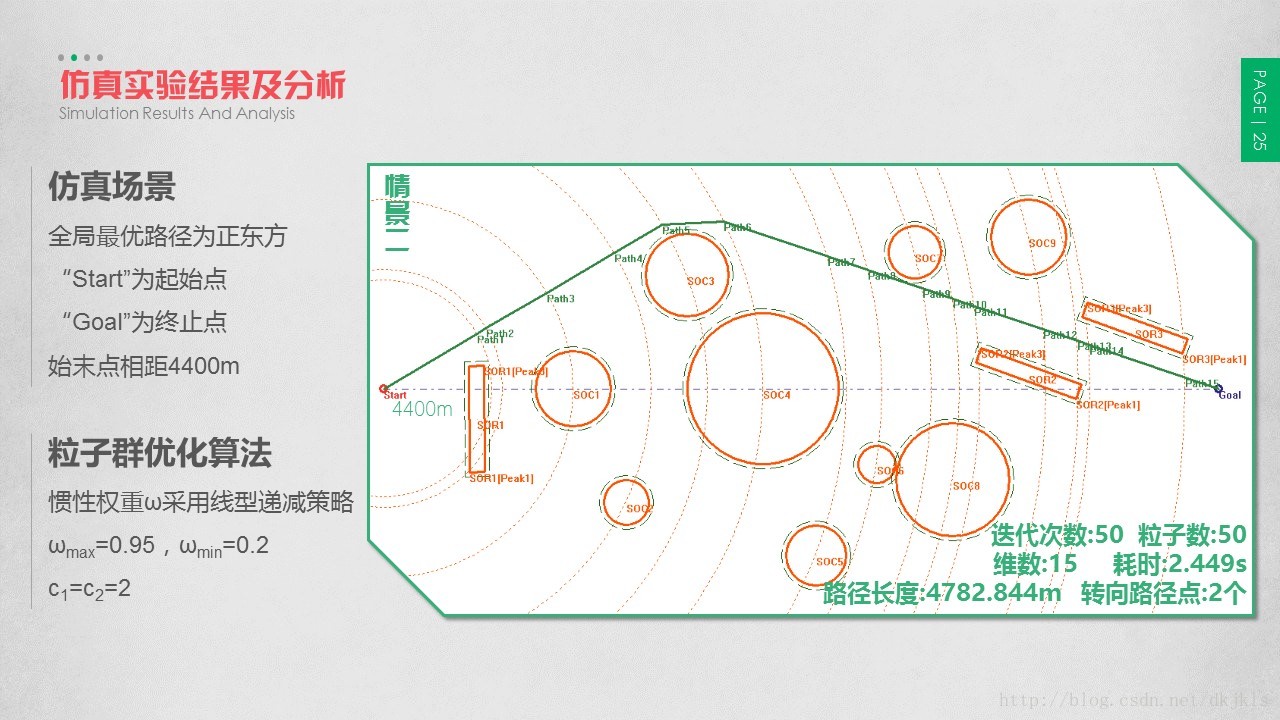
在本节仿真实验中,均假定水面无人艇的全局最优路径为正东方,“Start”为起始点,“Goal”为终止点,起始点和目标点之间的连线路径长度为4400m,运行速度为40Kn;惯性权重ω采用线型递减策略,且
ωmax
=0.95,
ωmin
=0.2;
c1
=
c2
=2。
仿真计算结果详见《第3章 基于PSO的已知静态路径规划方法》。
2.6 基于PSO并融合海事规则的已知动态路径规划
水面无人艇在航行期间,由硬件(如AIS、航海雷达等)可探测到在电子海图上没有标示的运动障碍物,并预测其运动信息。无人艇必须对这些已知静态障碍物进行规避,并符合国际海事避碰规则公约相关规则,使其能够快速、安全的到达终点或子目标点。本节将针对障碍信息已知的动态障碍物路径规划问题展开研究,将动态障碍物某一运动时刻转换为相对无人艇瞬时静止的,并实时的进行解算。最后通过仿真实验验证了本章所提出算法的可行性。
详见《第4章 基于PSO并融合海事规则的已知动态路径规划方法》。
2.6.1 国际海上避碰规则公约的约束
水面无人艇在海面航行过程中,为了避免对海上其它船只、人员的人身和财产安全,及无人艇自身的安全造成威胁,在进行避障的过程中必须满足一定的规则。国际海上避碰规则公约(International Regulations for Preventing Collisions At Sea,1972 / COLREGS),是由国际海事组织制定,为了防止、避免海事船舶相撞而制定的海上交通规则。但现在还没有专门的法律法规对水面无人艇的航行行为做出明确的指示,较为合理的解决方法就是使无人艇遵守国际海上避碰规则公约。
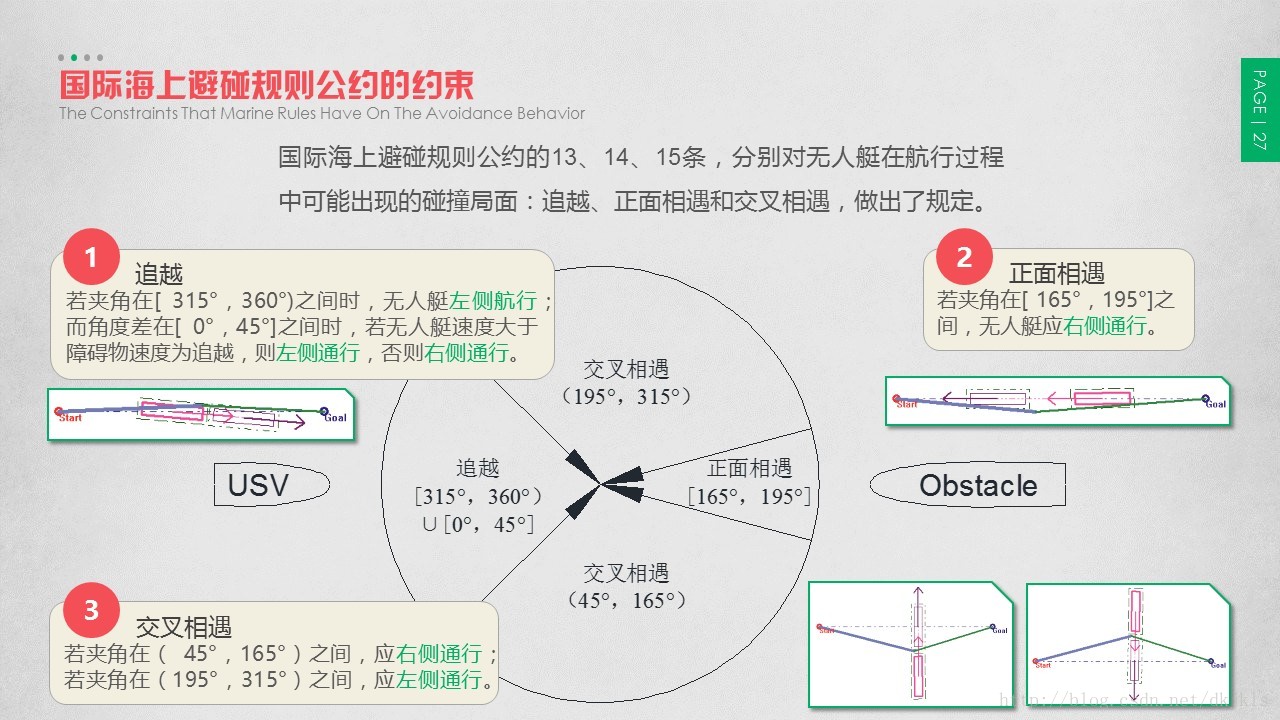
国际海上避碰规则公约的13、14、15条,分别对无人艇在航行过程中可能出现的碰撞局面:追越、正面相遇和交叉相遇,做出了规定。然而,这些规则只是针对船舶操作的一种行为约束,并没有明确给出在实际应用中的角度和范围。有关学者已经根据经验和大量测试,给定了相关的参数。下面将针对无人艇的实际情况,给出本文对国际海上避碰规则公约相关条例的具体说明,其中海事规则冲突情景定义见图。
避障模型示意图罗列了四种情况的避障模型,图中红色矩形障碍物为无人艇在起始点“Start”处探测到该障碍物的位置,箭头为其运动方向的指向,紫色障碍物则为无人艇对该障碍物避障结束时,障碍物所处的位置。
以下无人艇和运动障碍物之间的航向角度差,均以无人艇航向方向为基准(即航向角为0°)进行描述。
追越:若无人艇高速航行与障碍物航向角度差在[ 315°,360°)之间时,接近危险距离,则障碍物应该在无人艇的右舷,即无人艇左侧航行;而角度差在[ 0°,45°]之间时,若无人艇速度大于障碍物速度为追越,则左侧通行,否则右侧通行。
正面相遇:若夹角在[ 165°,195°]之间,接近危险距离,则无人艇同障碍物相遇碰撞,此时无人艇应右侧通行。
交叉相遇:若夹角在(45°,165°)之间,接近危险距离,则障碍物在无人艇右侧交叉相遇,此时无人艇应右侧通行;若夹角在(195°,315°)之间,接近危险距离,则障碍物在无人艇左侧交叉相遇,此时无人艇应左侧通行。
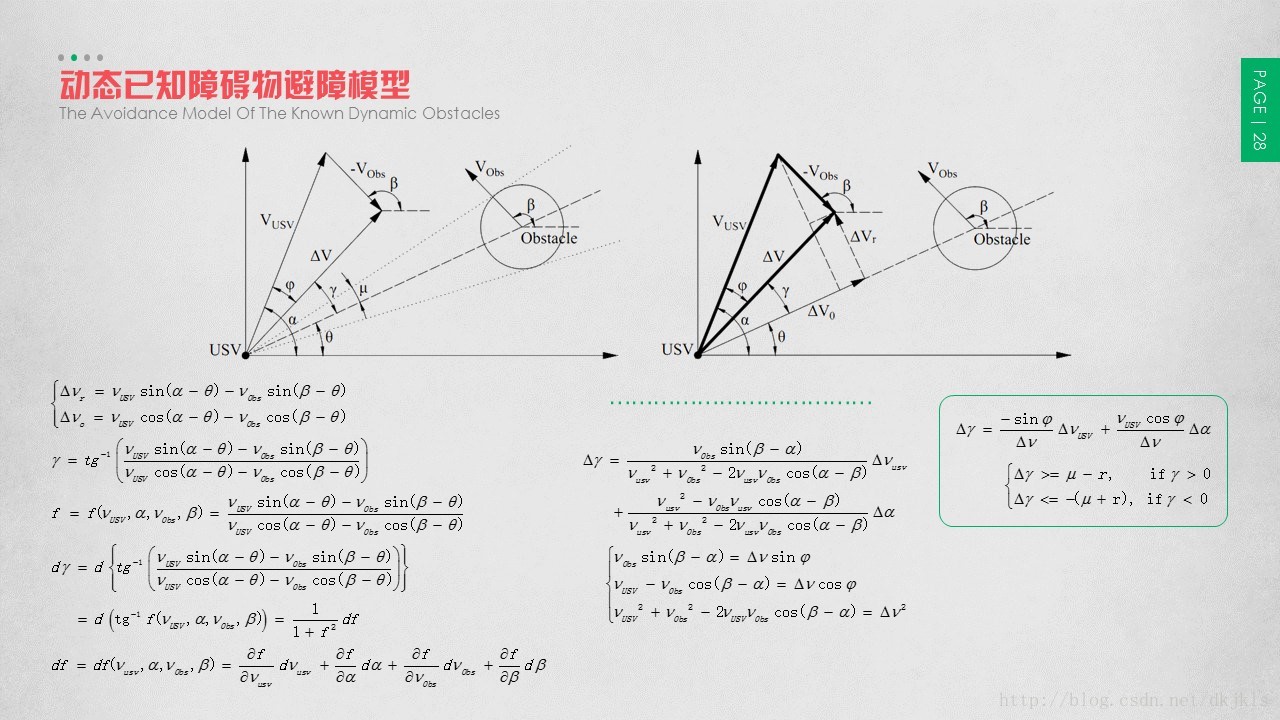
2.6.2 动态已知障碍物避障模型
首先考虑建立圆形障碍物几何模型。建立无人艇和障碍物当前位置的几何模型,如图4-1所示。图中无人艇和障碍物都是运动物体,
VUSV
是无人艇的运动速度,
VObz
是障碍物的运动速度。其中
α
为极轴到
VUSV
的角度,可表示为
α=∠(VUSV,ex)
,其中
ex
表示极轴;同理
β=∠(VObs,ex)
为极轴到
VObz
的转角;
θ=∠(LRO,ex)
为极轴到无人艇与障碍物圆心连线的转角;
φ=∠(VUSV,ΔV)
为
ΔV
到
VUSV
的转角;
γ=∠(ΔV,LRO)
,
μ=∠(LRO,tanL)
,tanL代表障碍圆切线。
为使无人艇能在下一时刻避开障碍区间,
γ
应该取在
(LRO−μ,LRO+μ)
范围之外的角度。下面将通过求解
γ
,找到无人艇航速和转向需要满足的条件,以实现无人艇避障。
将
Δν
分解为指向障碍物圆心的速度分量
Δν0
,和其垂直速度分量
Δνr
。其中
Δν0
促使无人艇朝向障碍物运动,
Δνr
促使无人艇逃离障碍物。
最后得出的公式说明了
Δγ
同无人艇的航速改变量
ΔνUSV
和航向改变量
Δα
存在关联,于是避障任务就转化成对无人艇此两值的求解。调整无人艇的航速
ΔνUSV
和航向
Δα
,分别对应了无人艇的两种有效避障行为,若仅仅采取其中的一个基本就能完成避障任务。
以上为建立圆形障碍物几何模型,及求解避障约束条件的过程;矩形障碍物几何模型的建立,及求解过程同圆形障碍物,在此不再赘述。
2.6.3 基于PSO算法的适应度函数的确定
无人艇在航行过程中,较多的使用的是不改变航速,仅改变航向的策略;但在某些情况下还需要同时改变航速和航向的策略,进行避障。该策略下是同时求解两个变量的最优值,无人艇路径规划问题就可以表达成一个多条件下的目标优化问题。
式中
φ
、
μ
、
γ
、
Δν
已知,
f(ΔνUSV,Δα)
为要实现最优的目标,即为粒子群优化算法中的适应度函数。且计算得到最优解后还需判断是否在可行域内,即需要满足国际海上避碰规则公约的约束的同时,还需要满足最优解不与已知静态障碍物相交。若该段路径中存在多个已知动态障碍物,则只需对每个障碍物加入式中第二、三个约束即可。
此粒子群优化算法适应度函数
f(ΔνUSV,Δα)
的选取,是考虑到尽可能少地改变已知静态环境下规划的最优路径和运动状态(包括航行速度和航向)。因已知静态环境下规划的最优路径已经包含了全局优化信息,所以已知动态算法就没有过多的考虑全局优化目标了。
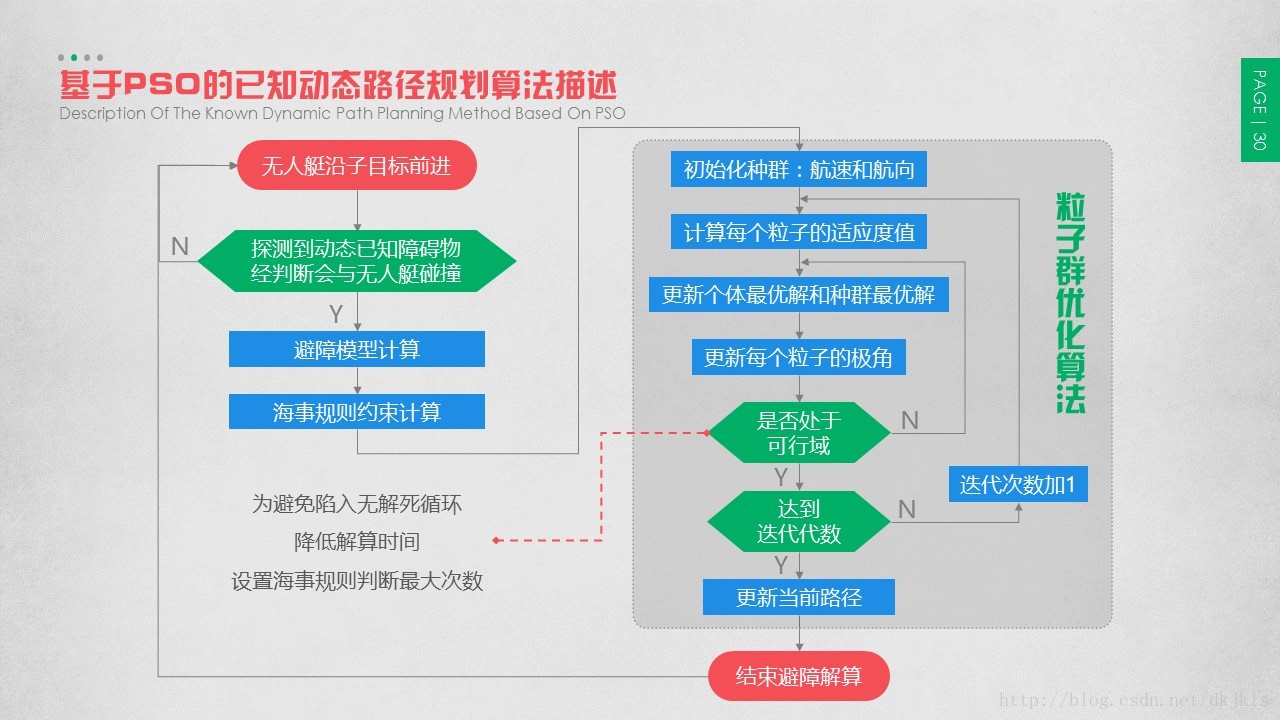
2.6.4 基于PSO的已知动态路径规划算法描述
在粒子群优化算法中,可行域判断是指要同时满足对静态已知障碍物的规避,和对符合海事规则约束的动态已知障碍物的规避,以及对无人艇最小回转直径的限制。还需要说明的是,在粒子群优化算法中,对无人艇采取海事规则约束时,需设定一个海事规则判断最大次数,若大于此值,就放弃采用海事规则约束,以免陷入局部最优,从而达到降低解算时间,实时快速避障的目的。
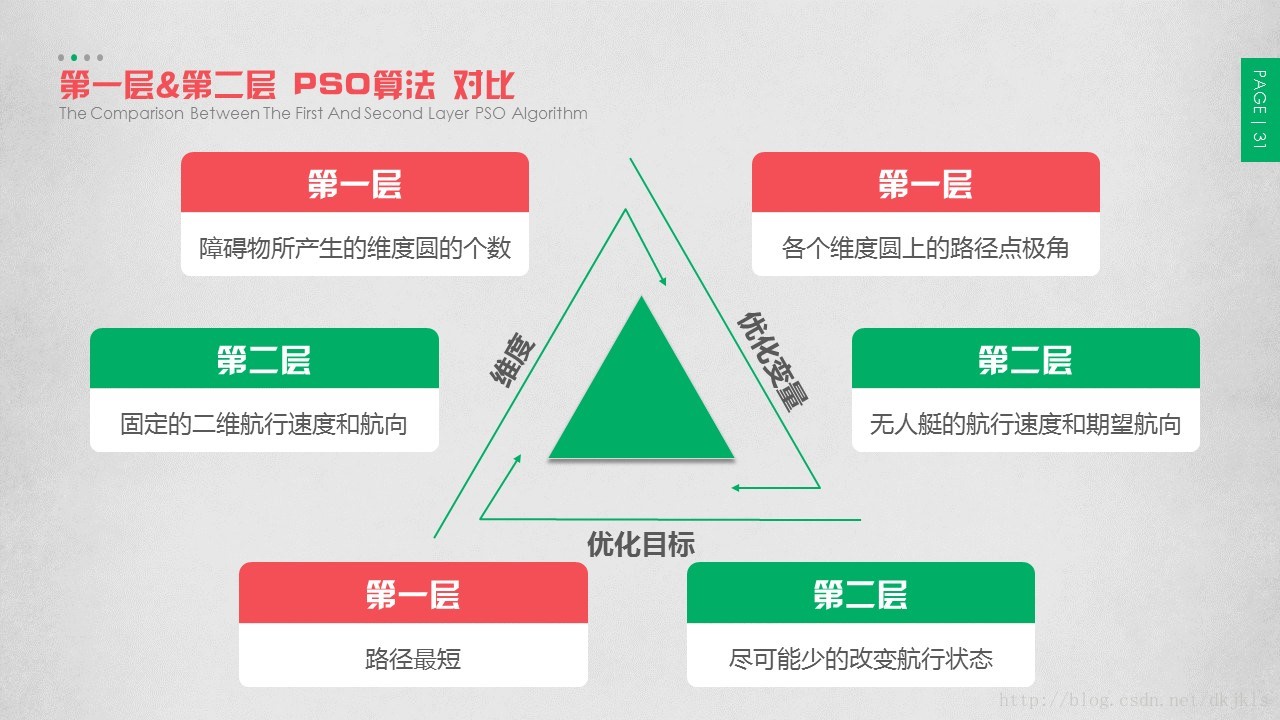
2.6.5 第一层&第二层 PSO算法 对比
本文所提出的已知动态路径规划方法,是基于粒子群优化算法进行的,与上一章采用PSO算法不同的是:上一章粒子群算法是针对所有静态障碍物而言的,其维度是障碍物所产生的维度圆的个数,随着环境中静态障碍物的变化而改变的,且其优化调整变量为各个维度圆上的路径点极角;而本章粒子群算法则是针对子目标段的运动障碍物而言的,其维度数是固定的二维,分别为无人艇的航行速度和期望航向,且其优化调整变量即为这两个值。
与上一节相对比,优化的目标也不尽相同。上一章PSO算法的优化目标为路径最短或能量消耗最少;本章采用的PSO算法优化目标则为,在考虑了海事规则的前提下尽快逃离障碍物的运动区域。
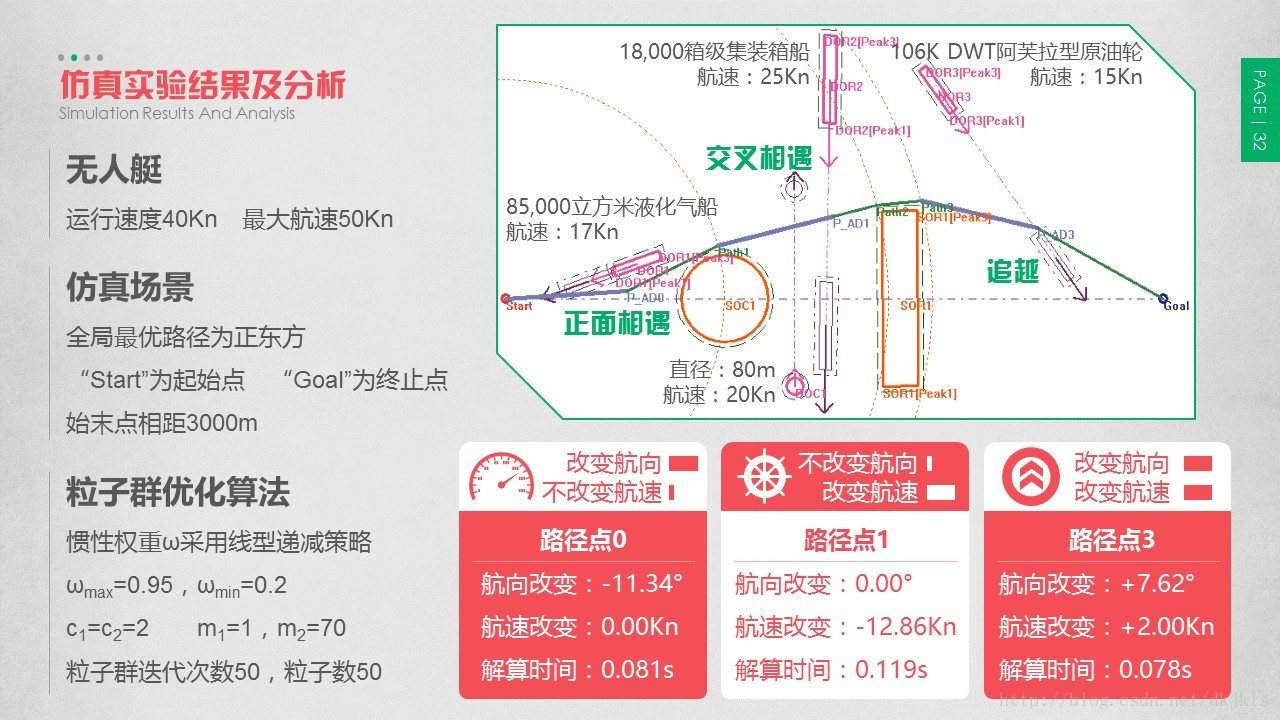
2.6.6 仿真实验结果及分析
在本节仿真实验中,假定水面无人艇的全局最优路径为正东方,“Start”为起始点,“Goal”为终止点,始末点相距3000m;无人艇运行速度为40Kn,最大航速为50Kn。粒子群优化算法中惯性权重ω采用线型递减策略,且
ωmax
=0.95,
ωmin
=0.2;
c1
=
c2
=2;
m1
=1,
m2
=70;设置粒子群迭代次数50,粒子数50。
该环境下还包括一个已知动态圆形障碍物DOC1,和三个已知动态矩形障碍物DOR1、DOR2、DOR3。三个已知动态矩形障碍物,分别选取为上海外高桥制造的85,000立方米液化气船,18,000箱级集装箱船和106K DWT阿芙拉型原油轮。该环境下,为了方便计算,将动态障碍物的起始时刻位置均定为无人艇起始点时刻的位置。动态障碍物起始时刻的位置用粉红色进行表示,避障结束点时刻障碍物的位置用紫色进行表示,箭头方向即为障碍物运动方向。
经过第二层基于PSO并融合海事规则的已知动态路径规划方法解算,得到已知动态环境规划路径信息,路径节点相对于已知静态路径的改变量见表4-6所示,路径节点及无人艇航速和解算该段路径的耗时见表4-7所示。下面将对该环境下的已知动态避障进行简要的说明。
无人艇在起始时刻时,探测到已知动态矩形障碍物DOR1,并与无人艇呈185.17°相向运行,即夹角在[ 165°,195°]之间,为海事规则中的正面相遇情形。若无人艇不做改变继续向前行进,会同障碍物相遇碰撞,所以需要无人艇作出相应的调整,从障碍物左舷即无人艇右转向通行。所以无人艇在起始时刻就进行已知动态障碍物避障,通过该算法解算,耗时0.081s,得到的避障方法为向右舷转向11.34°,航速不变行进。无人艇运行到避障结束点后,就已成功完成了对障碍物DOR1的规避,此时便转向朝向本段的子目标点Path1行进。
无人艇继续运行到Path1位置时,探测到已知动态矩形障碍物DOR2,和已知动态圆形障碍物DOC1,并分别从无人艇两侧驶来,角度分别为75.17°和254.17°,为海事规则中的交叉相遇情形,需要分别从两个障碍物的后方通过,即对DOC1而言为右侧通行,对DOR2为左侧通行。无人艇在Path1时刻进行已知动态障碍物避障,通过该算法解算,耗时0.119s,得到的避障方法为航向不进行改变,航速从40Kn减少到27.14Kn行进。无人艇运行到避障结束点后,就已成功完成了对障碍物DOR2和DOC1的规避,此时便逐渐加速到40Kn继续朝向本段的子目标点Path2行进。
无人艇继续运行到Path3位置时,探测到已知动态矩形障碍物DOR3,并与无人艇呈32.06°运行,即角度差在[ 0°,45°]之间时,且无人艇速度(40Kn)大于障碍物速度(15Kn),为海事规则中的追越情形。此时需要无人艇作出相应的调整,从障碍物左舷即无人艇左转向通行。无人艇在Path3时刻进行已知动态障碍物避障,通过该算法解算,耗时0.078s,得到的避障方法为向左舷转向7.62°,航速增加到40.2Kn行进。无人艇运行到避障结束点后,就已成功完成了对障碍物DOR3的规避,此时便转向朝向本段的子目标点即终止点行进。
仿真计算结果详见《第4章 基于PSO并融合海事规则的已知动态路径规划方法》。
3 场地布局算法
3.1 场地布局问题描述
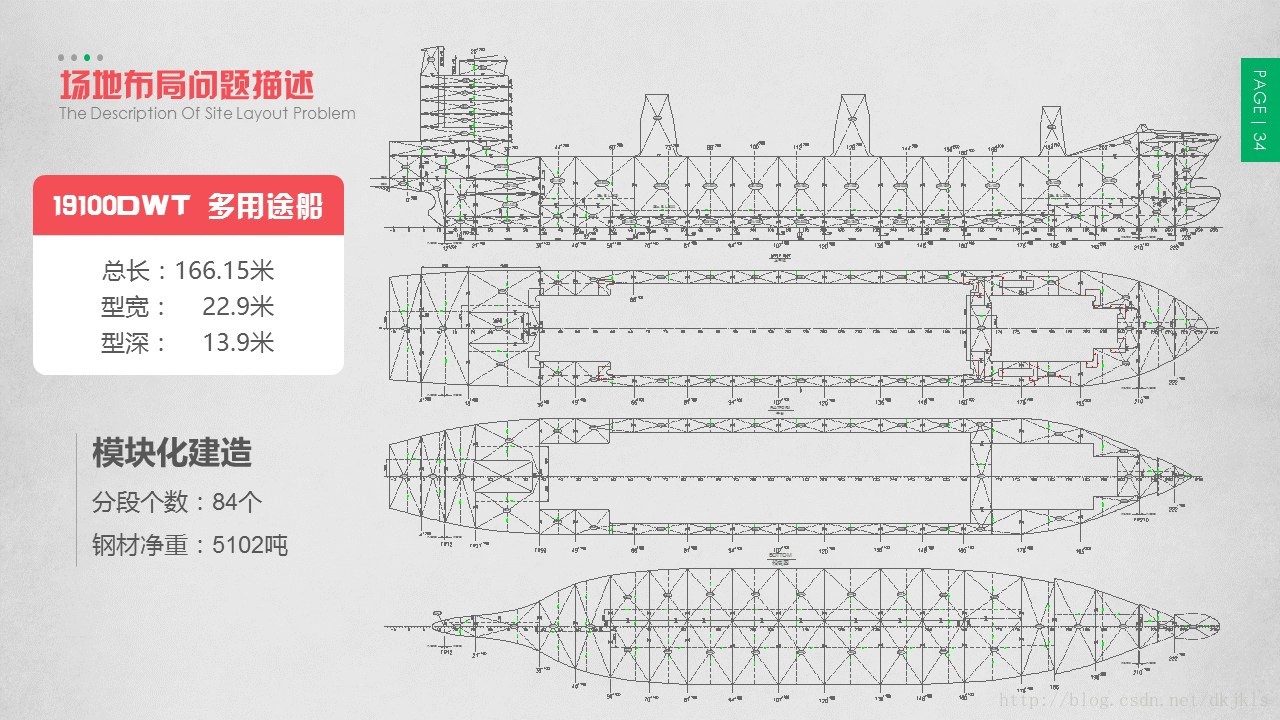
由于船舶的尺寸、重量非常大,为了缩短造船周期,且使高空作业平面化等,将船舶按照结构分成若干个分段进行建造。就如同互联网应用中,将庞大的服务拆分成各个不互相耦合的微服务。
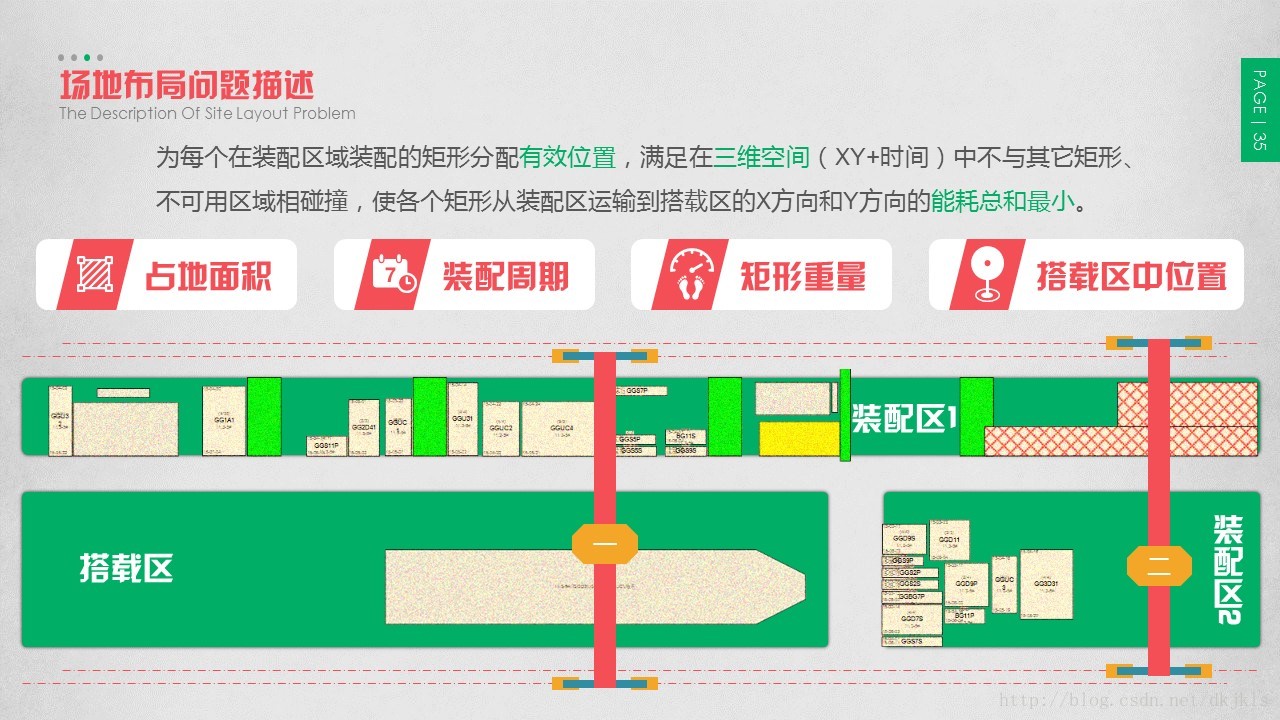
场地共分为两大区域:搭载区和装配区。搭载区中各个矩形块即为该问题中的建造资源,而各个建造资源所组成的多边形即为最终的产品,每个矩形块在搭载区中的位置即为该矩形块在该问题中的目标位置(已知条件)。各个矩形块为了能运输到搭载区进行总装,需要预先在装配区完成一系列的装配作业,每个矩形块因各自的装配作业不同,在装配区中装配的周期(已知条件,矩形块中t参数)也不尽相同;每个矩形块在装配区中的布局(待求解)需要满足的条件包括:矩形块不与其他矩形块相干涉,不与装配区中障碍物(现实中用来运输相关资源的绿色通道)相干涉,布局不超越装配区。而矩形块从装配区运输到搭载区,运输的方向仅能为水平的X方向和垂直的Y方向。
需要解决的优化问题可描述为:为每个在装配区装配的矩形块分配有效位置,使各个矩形块从装配区运输到搭载区的X方向和Y方向的能量总和最小。
3.2 场地布局算法参数确定
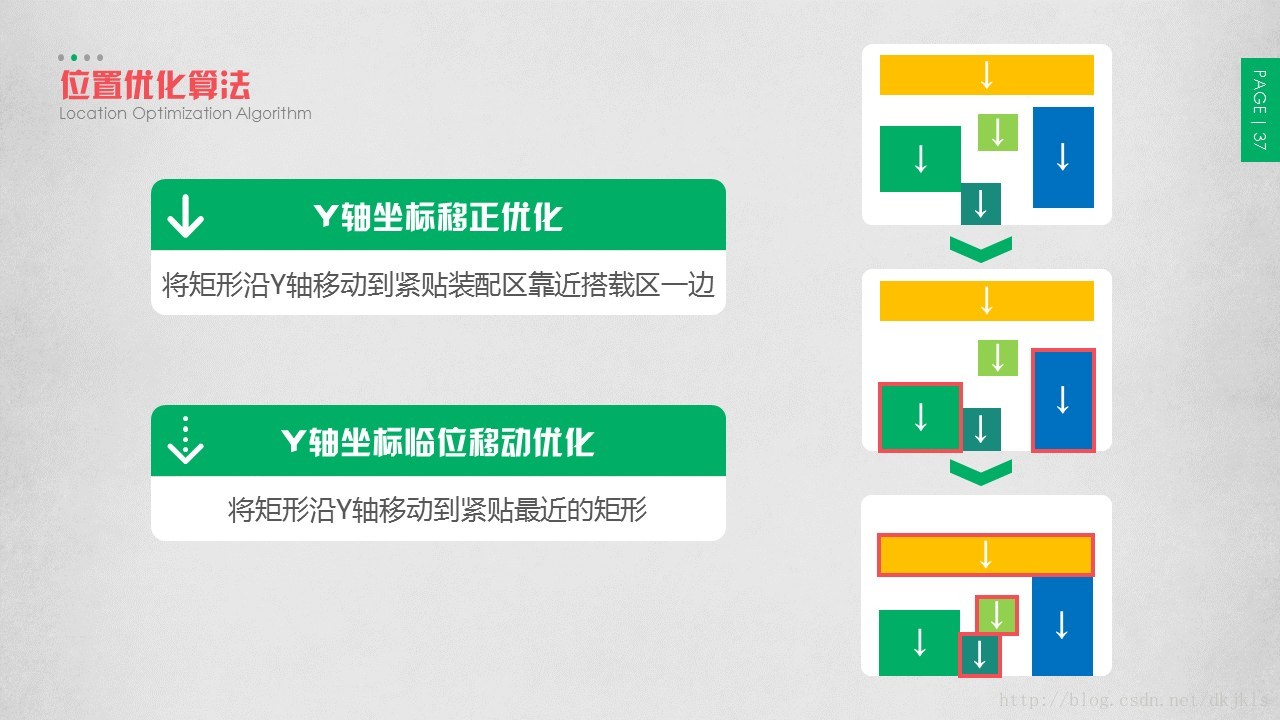
3.3 位置优化算法
由装配区与搭载区布局形式可知,较优的布局方案会紧贴距搭载区较近的一边。因此,为将布局结果与区域布局形式相结合,得到更符合实际的最优结果,加入位置优化算法策略。图中示例取搭载区位于装配区正下方。
图中示例取搭载区位于装配区正下方。
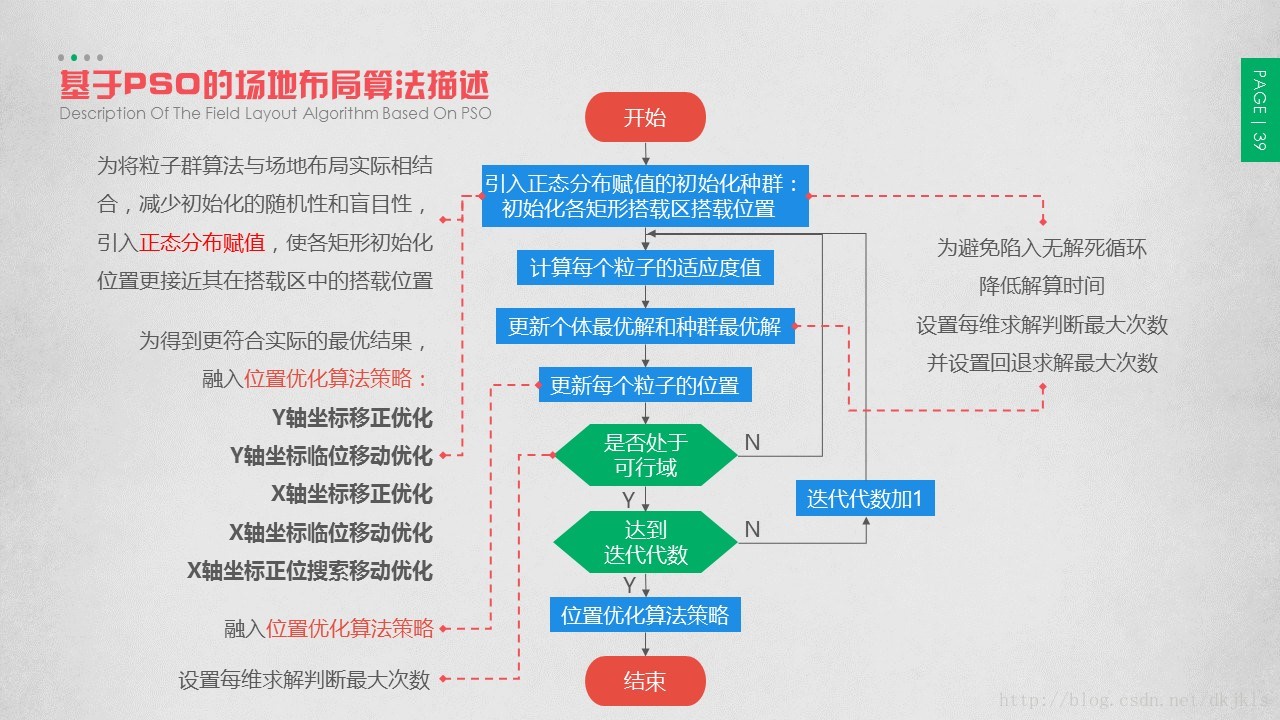
3.4 基于PSO的场地布局算法描述
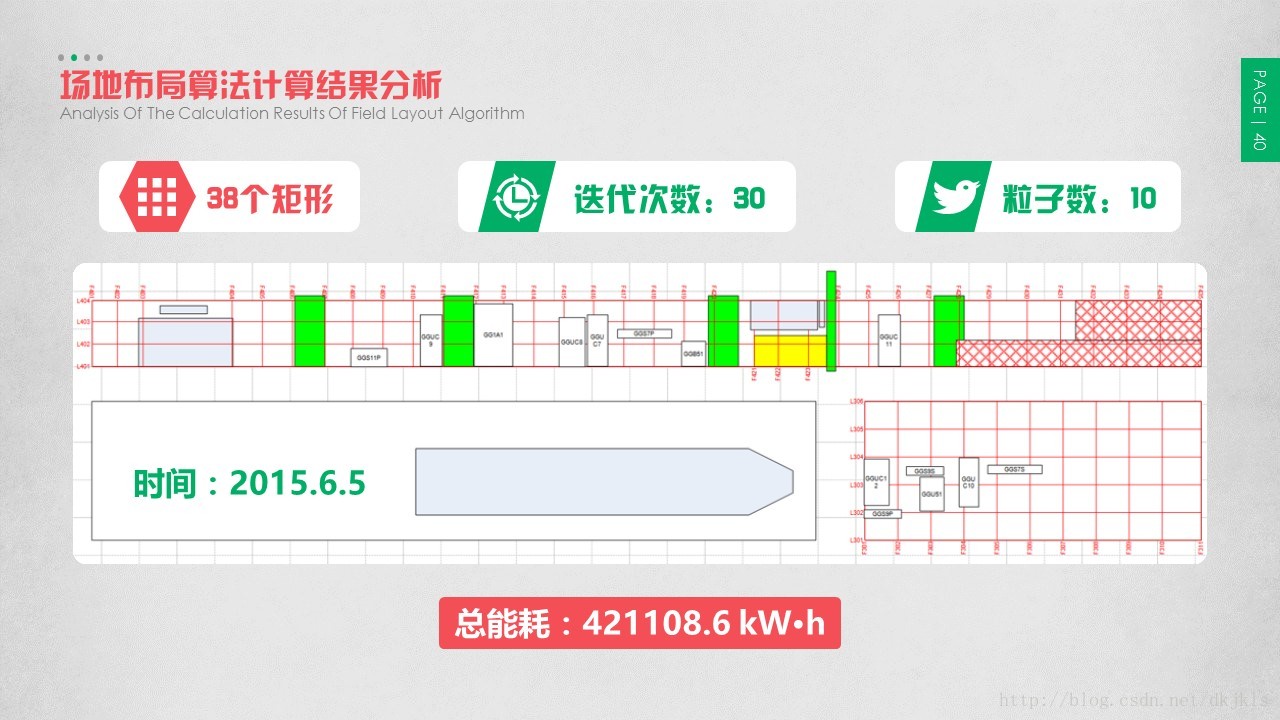
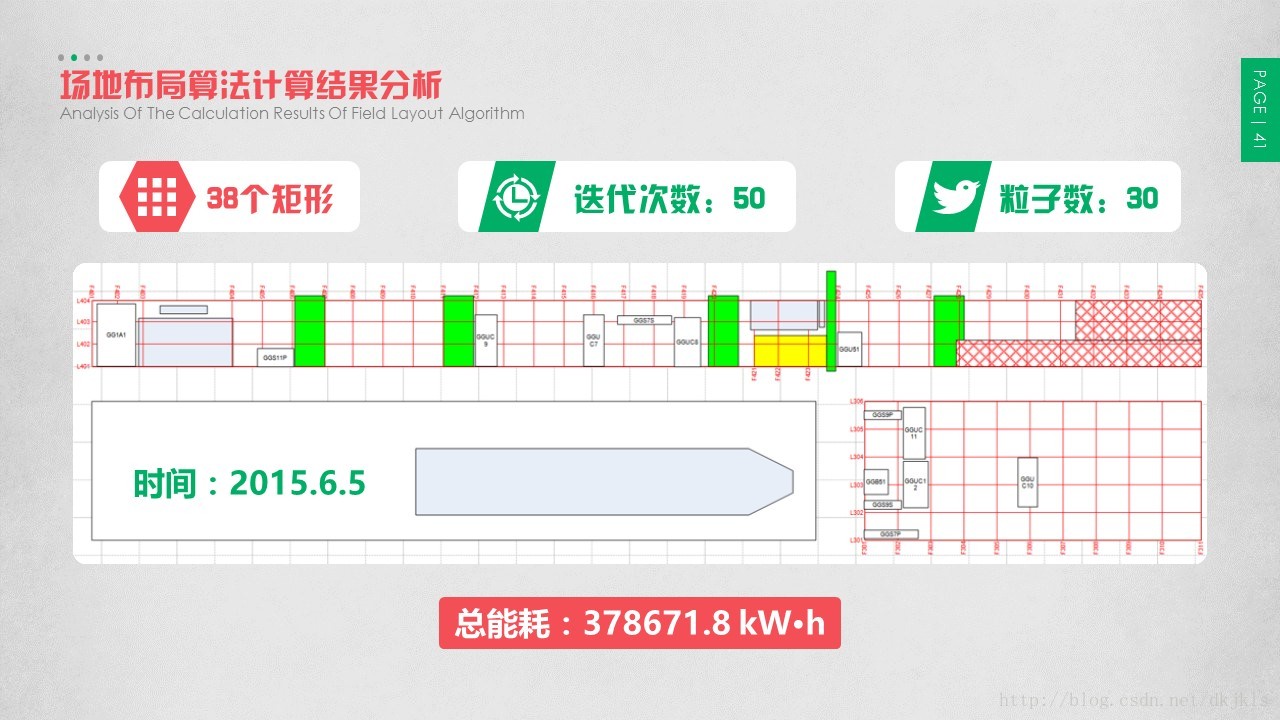
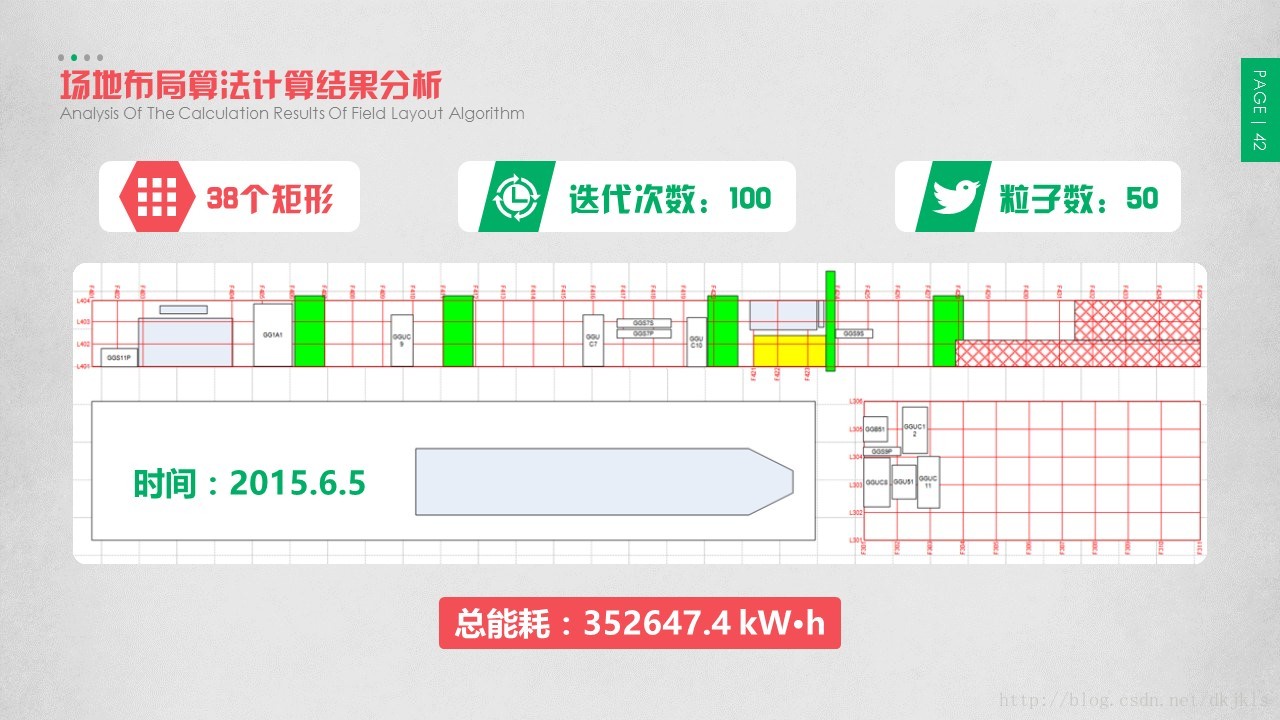
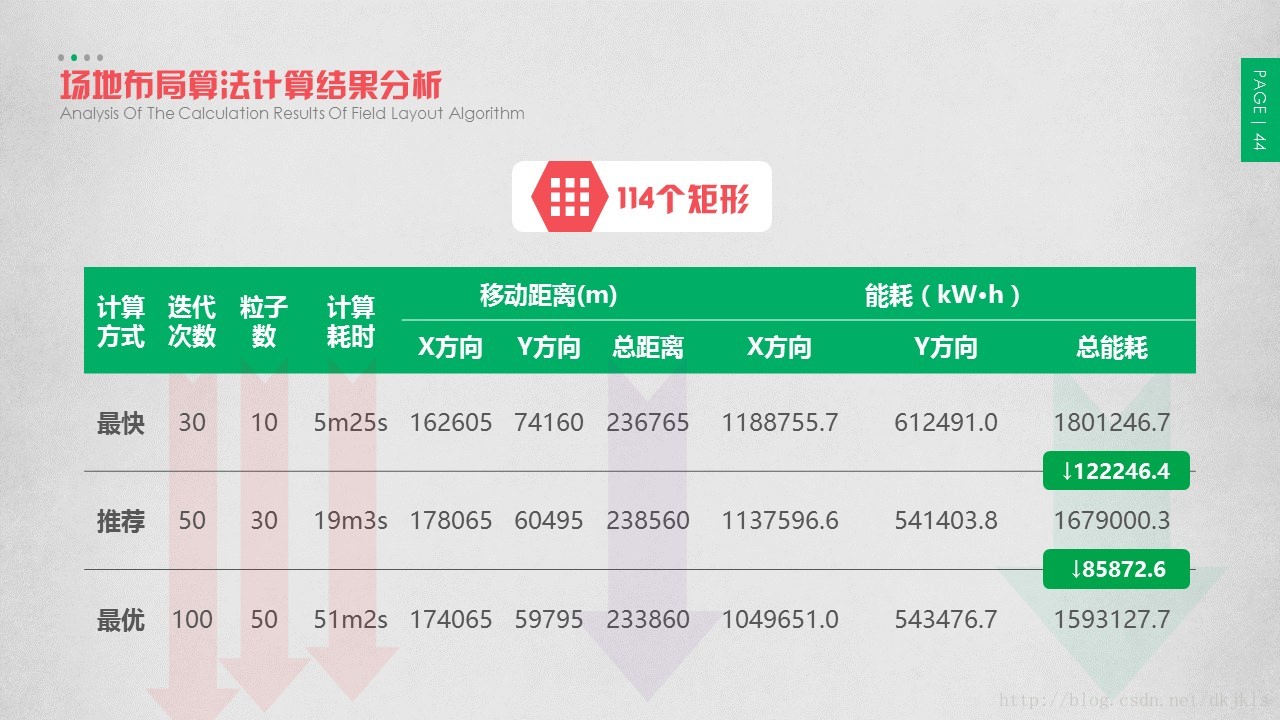
3.5 场地布局算法计算结果分析
采用上述描述的算法对模拟数据进行计算。由于算法原始程序未进行优化,后续实践中发现仅对算法进行代码级别的优化,即可实现计算耗时的大幅缩短,因此计算结果中的计算耗时仅代表相对计算耗时值。
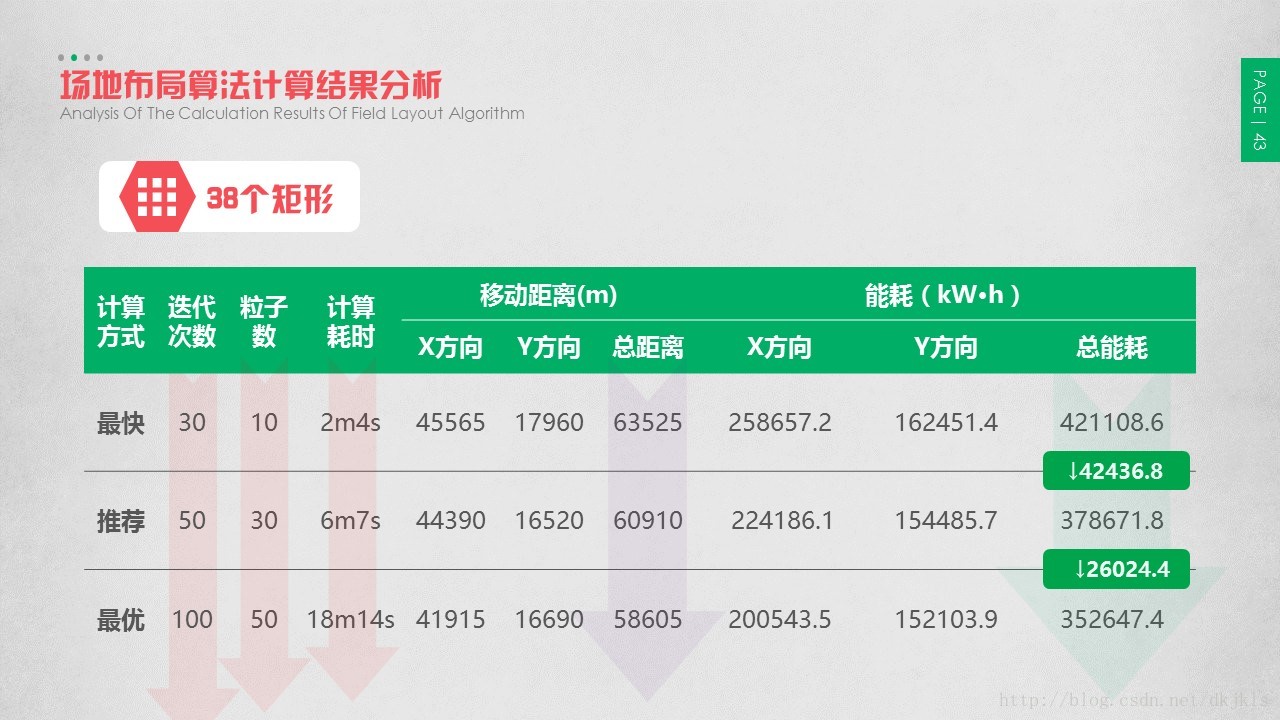
由计算结果可知,随着算法的迭代次数、粒子数不断增加,计算耗时不断增加,而总能耗则不断降低。
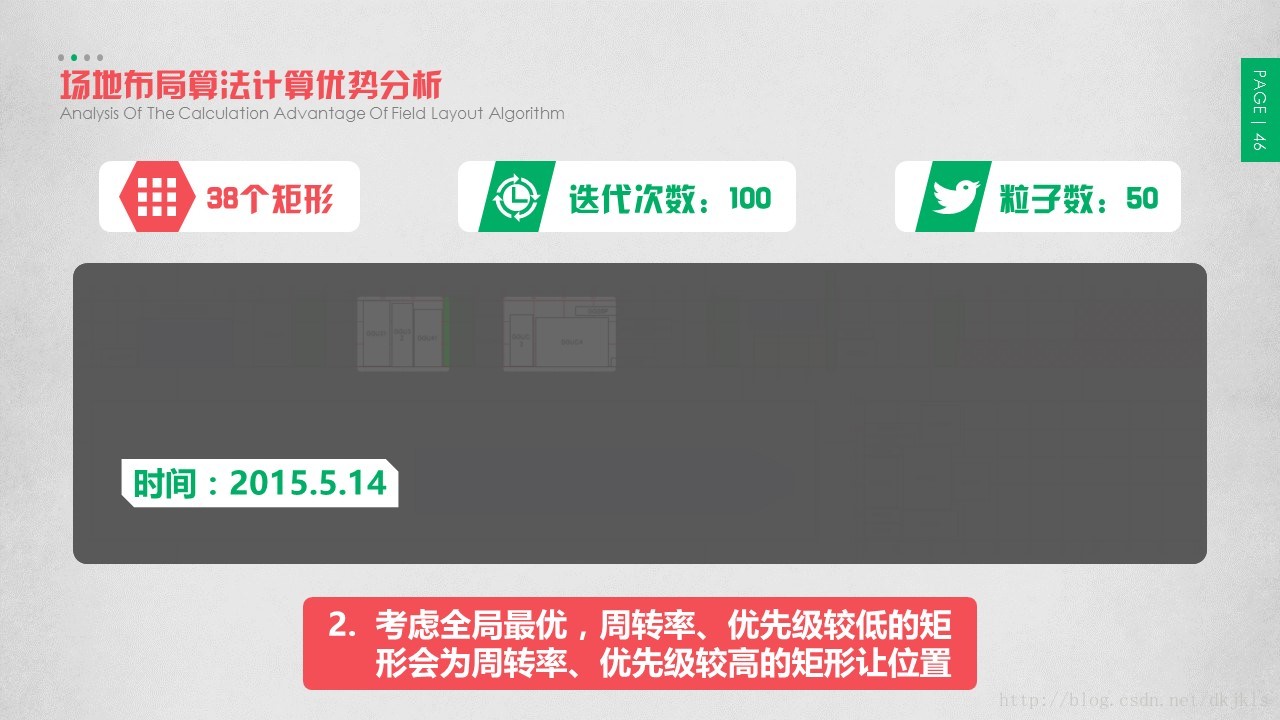
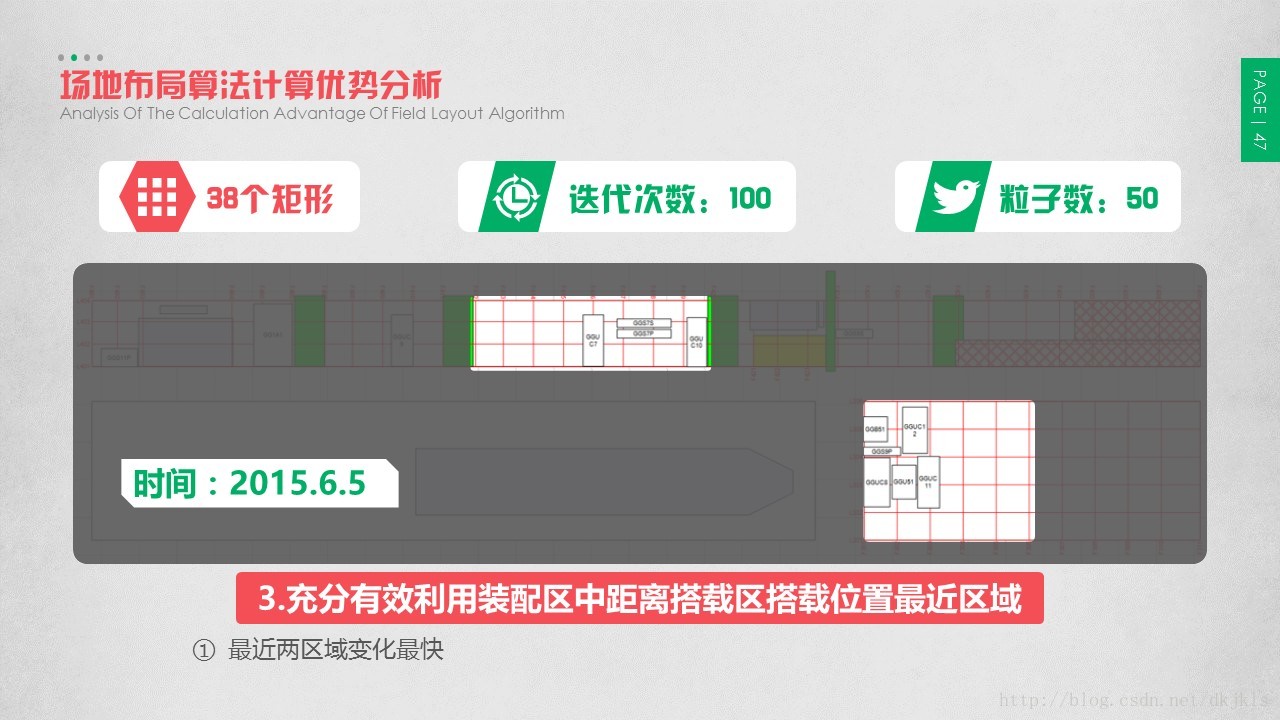
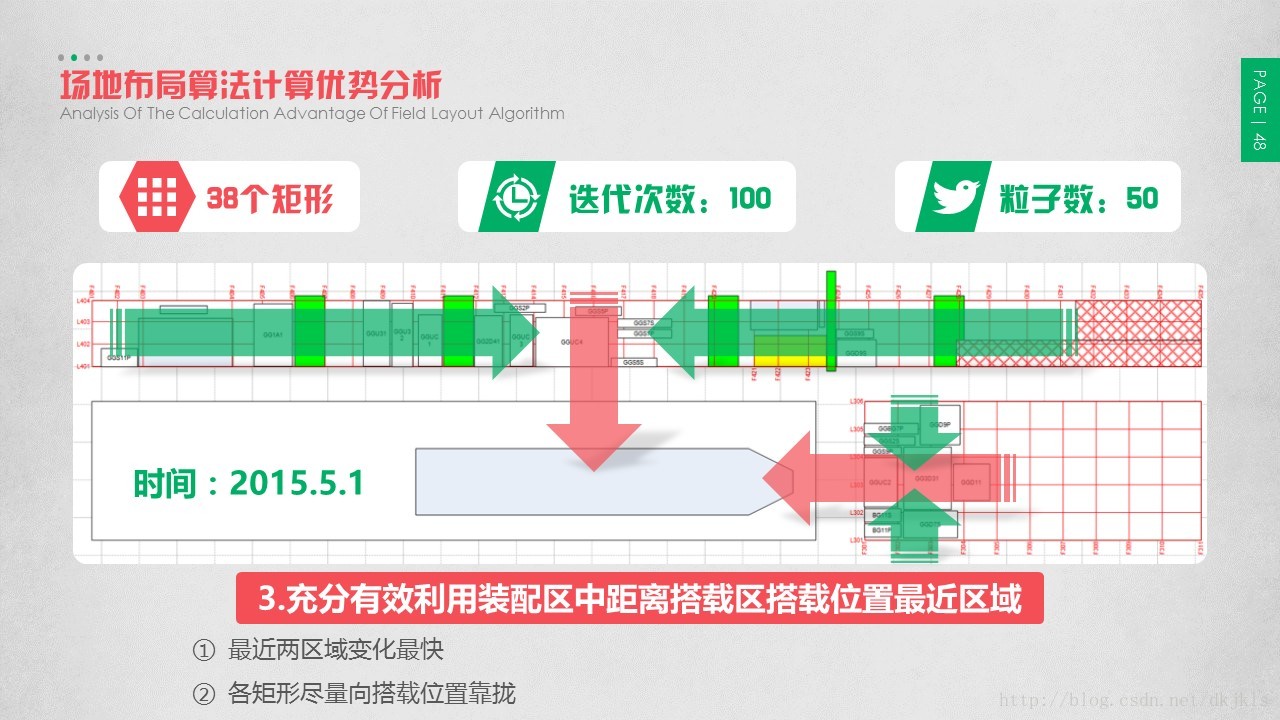
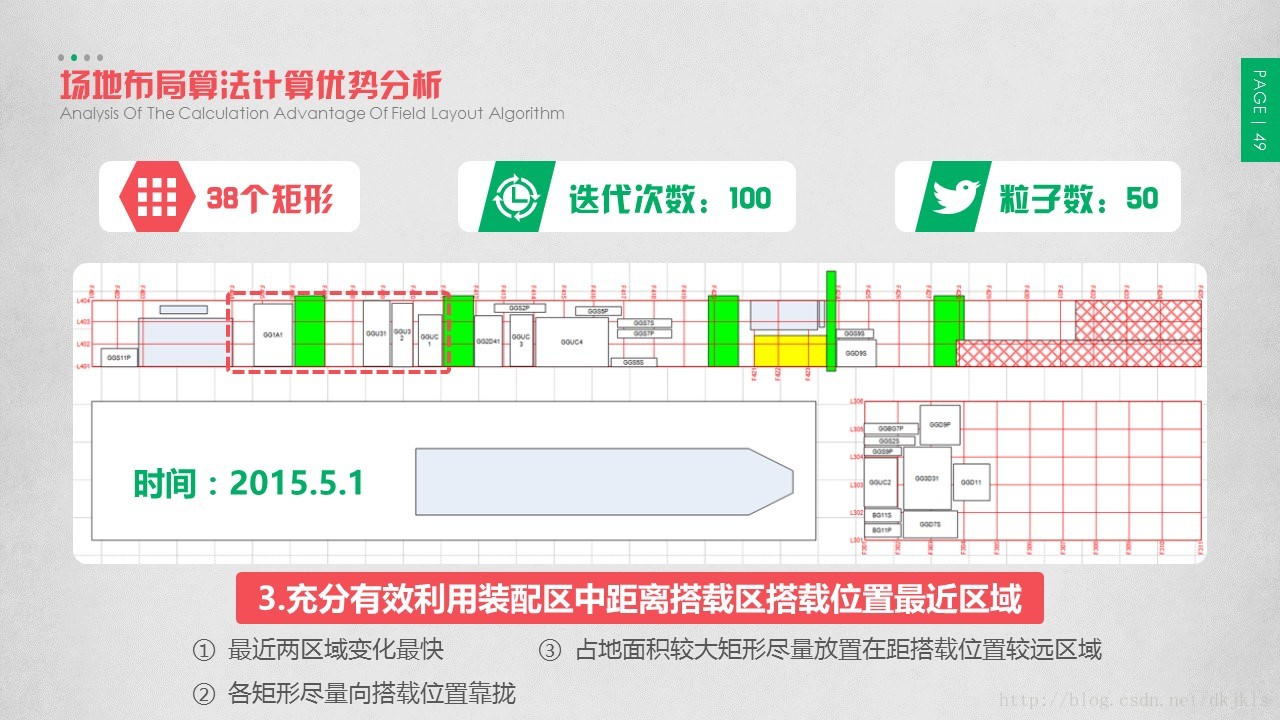
3.6 场地布局算法计算优势分析
3.7 场地布局算法的不足及仍需探讨的问题
通过算法的计算结果,可以初步判定该算法还是可以解决场地资源布局问题的,当然该算法还不是很完善,仍有很多问题需要探讨。
4 算法对比及总结
4.1 三种算法对比
4.2 总结
==============文档信息===============
版权声明:本文为博主原创文章,未经博主允许不得转载
署名(BY) :dkjkls(dkj卡洛斯)
文章出处:http://blog.csdn.net/dkjkls









 本文深入探讨了粒子群优化算法(PSO)在水面无人艇避障与场地布局中的应用。详细介绍了PSO算法原理、二维示例及其迭代公式,并通过实例展示了PSO在静态与动态障碍物规避中的有效性。此外,还介绍了PSO在场地布局问题中的解决方案。
本文深入探讨了粒子群优化算法(PSO)在水面无人艇避障与场地布局中的应用。详细介绍了PSO算法原理、二维示例及其迭代公式,并通过实例展示了PSO在静态与动态障碍物规避中的有效性。此外,还介绍了PSO在场地布局问题中的解决方案。










































 15万+
15万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








