Spark一些常用的数据处理方法-3.MLlib的模型（还没写完）

因为mllib属于基础库，且本系列主要作为普及性文章，所以我不打算更新相关原理及其数学关系，有兴趣自学的童鞋可以去网上翻，基本原理都是一样的。

3.1 什么叫模型

我理解的模型，就是对现实业务的一种数字化抽象。它既可以是一套数学公式的各种参数组合，也可以是一种多维向量的数字化呈现，就是特征与数量的关系。

3.2 MLlib模型转为PMML模型

PMML模型就相当于数据库中的csv文件之类的东西，所有支持标准PMML解析的工具都能够使用。使用方法也非常简单
model.toPMML("PATH")

3.3 线性模型

线性模型即是凸优化的相关问题，对于凸优化方面，推荐大家参考一下《凸优化》，Stephen Boyd, Lieven Vandenberghe著，王书宁、许鋆、黄晓霖译，清华大学出版社的那本书，比较有启发。不过讲的是纯数学的东西，基础稍差的童鞋可以慢慢看。这部分还可以参考一下这位大神的博客http://blog.csdn.net/xiazdong/article/details/7950084，我觉得写的还是非常非常通俗易懂的。
线性模型中最常用的应该是线性回归模型了，也就是所谓的知道x和y，求y=神马x这个公式的过程。由于这个公式是“拟合”出来的，换句话来说就是猜的，所以有一个过拟合的说法。
什么叫过拟合？简单来说，在xy坐标系中，给你2个点，我们很容易的写出y=ax+b这样的公式，也就是说有一条线可以链接两个点；如果给你10个点，让你去做它的公式，那么自然是一个公式涵盖10个点是最准确的，一般可能会是一条曲线，但还是可以写出来的；但是如果给你10000个点，再去做它的公式，想必就非常的困难了。所以我们需要把这个公式“拟合”出来，换句话就是不要求最准确的，而要求近似的用一个公式相对准确的描述所有的点。
这种拟合出来的线如果是直线，那么就叫做线性回归，也算是拟合的一个简单的特例，那种用最小二乘法就可以很方便算出来。但一般都是用曲线，所以更常用的是梯度下降。
既然公式是“拟合”出来的，那么公式所画出来的线上的点与实际的点相差多少是可接受的呢？这便引出了“损失函数”。损失函数是衡量拟合出来线上的点与实际的点差距的函数。这个“损失”自然越低，拟合的效果越好。
这个损失函数与其系数的关系大概是这样的。（从网上搞的）

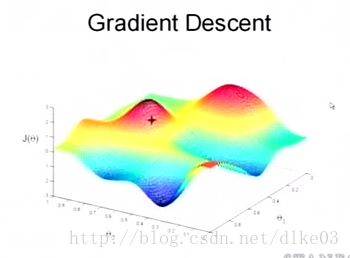
如果习惯看2D那种“地形图”的可以出门左拐百度，这个是个3D的图，我觉得对于基础较弱的童鞋看着更为直观。我们可以发现红色的就是误差较高的函数系数所对应的结果，蓝色部分就是误差较低的，也是我们想要的。这便引出了“梯度下降法”。
梯度下降法简单理解就是我指定一个点，然后按照指定的长度移动，直至移动到最低谷的一种方法（由图可知，这跟切线斜率有关，判断的标准自然是导数的变化）。我觉得从凸优化的角度理解就是相当于在坐标系里面画一个凸多边形，从一个端点不停移动直至找到另一个所需端点的过程。当然，在凸多边形是能够得到唯一的结果，而在这张图里我们可以看到，低谷可能不止一个，所以梯度下降得到的最低点的结果可能不是全局的最低点。所以在使用中需要仔细考虑数据所带来的损失函数的情况，尽量将这个函数变成凸函数。
（代码部分未完待续）