Bezier曲线的de Casteljau算法证明

ezier曲线（又称貝茲曲線或贝塞尔曲线）的定义和性质请看维基百科貝茲曲線。它的定义是：

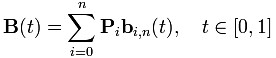
其中，

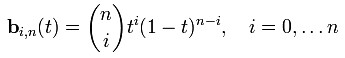，约定0⁰ = 1.

 

e Casteljau算法揭示了Bezier数学上很美的一个性质，我八成相信是先有了这个性质，才有了上面的定义式，当然它们是等价的。首先来看维基百科中的三张图：

二次Bezier曲线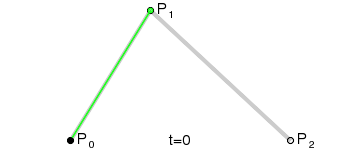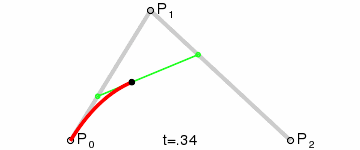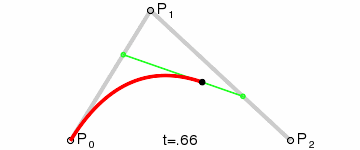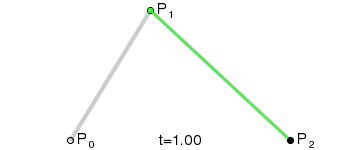

三次Bezier曲线：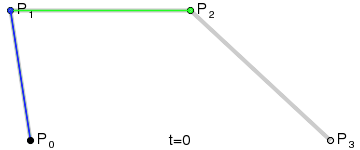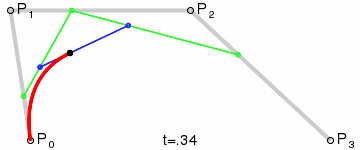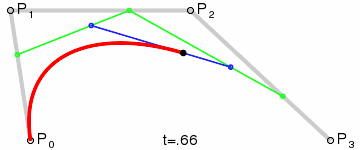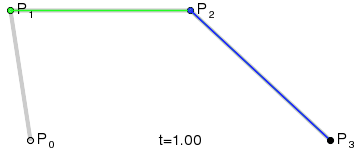

四次Bezier曲线：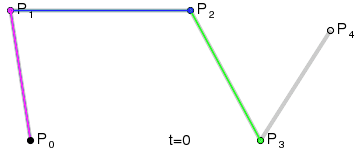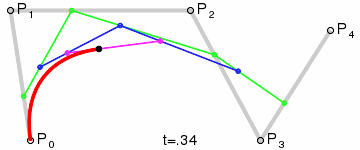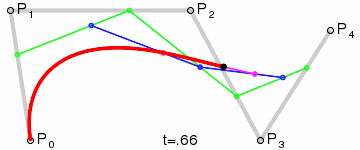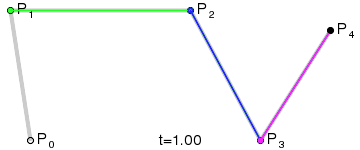

这三张图展现了Bezier曲线漂亮的数学性质。图中的参数变量t的从0增长到1，红色的线就是Bezier曲线，Bezier曲线上的任一个点(t)，都是其它相邻线段的同等比例(t)点处的连线，再取同等比例(t)的点再连线，一直取到最后那条线段的同等比例(t)处，该点就是Beizer曲线上的点(t). 以二次Bezier曲线为例，如该曲线上的1/3点，就是线段P0P1取1/3点，P1P2取1/3点，两点连线，再取其1/3点处即是。这就是de Casteljau算法提出来的，其数学表达式是：

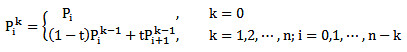
上式中，k表示第k层，以四次Bezier曲线为例，k=0时，就是灰色线段，k=1时，就是绿色线段，k=2就是蓝色线段，一直递推下去就是Bezier上的点(t)了。于是用de Casteljau算法很容易求出Bezier曲线上的任一点(t)的位置。换一种图示的方法表示这种递推关系：

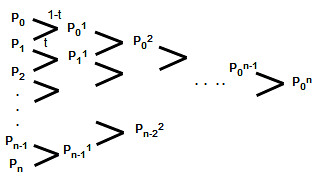
这是用几何画板画的，很难看，解释一下。左边一列是原来(k=0)的控制顶点，第二列是(k=1)的控制顶点，以此类推。每个箭头表示两个点分别乘以1-t和t并加起来，得到右边的点。这样一直做到最后的点就是Bezier上的点(t).

先看P0的系数为什么是，因为每次P0都是乘以(1-t)传到右边的点，这样一直传了n次到达最右端。仔细看一下就可以发现，最左边的点传递到最右边，是靠乘以一系列的t或1-t到达的，那么Pi的系数就是Pi走到最右边左右的"路"的系数之和。比如，P0只能一直走斜下的边，而且只有一条路，记住能不往左走，因此它的系数就是。那么P1的系数就是,因为它到最右边有两条路，且t和1-t的次数是一样的。可以发现每个Pi的每条路的t和1-t的次数都是一样的，而路的条数的系数很熟悉。没错，把上图逆时钟转90°就是杨辉三角了。

杨辉三角有这样的特征：每个数字表示从顶点走下来到该点不同走法的数目，而且无论是哪条路走到该点，向左和向右的次数是一样的，等于该点的二次多项式展开系数。

到了这里，如果看懂了的话，我想已经证明了，剩下就是一些说明性言语了。数学美还没结束，见下图：

 

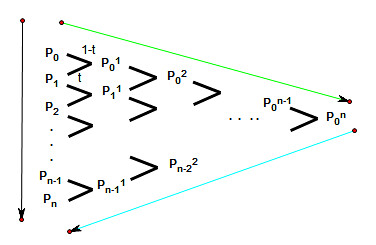
绿色线按顺序排列的点P0到P0n这n个点可以画出一条n次Bezier曲线，记为B1；蓝色的n个点也可以画出一条n次Bezier曲线；这两条曲线直接接起来，就是原来P0到Pn画出的n次Bezier曲线！神奇吧，它们居然有类似向量的性质。实际应用也是用这个性质，一般取t=1/2，将一条Bezier曲线变成两条小的，再继续分下去，当Bezier曲线足够小时就可以用线段代替曲线了。这个性质同样可以证明，但写到网上很麻烦就不写了，大家推荐好一点的数学画图软件，谢谢。数学有时很美。