简单理解红黑树

前言

在计算机领域，数据的处理能力是非常重要的，查找作为一种对数据处理一个很重要的能力，我们就先来看看今天要说的红黑树

查找

说到查找我们很快就能想起来很多常用的查找方式，比如说遍历，二分查找，哈希等，其中我们知道哈希在一定情况下可以达到O（1）的时间复杂度，速度可谓是非常之快，但是他也有他的缺点就是不能范围查找，所以我们就来说说今天要说的红黑树。

二叉查找树

说到红黑树，我们不得不先说一下二叉查找树，因为红黑树是在他的基础上建立的，下图就是一颗二叉查找树

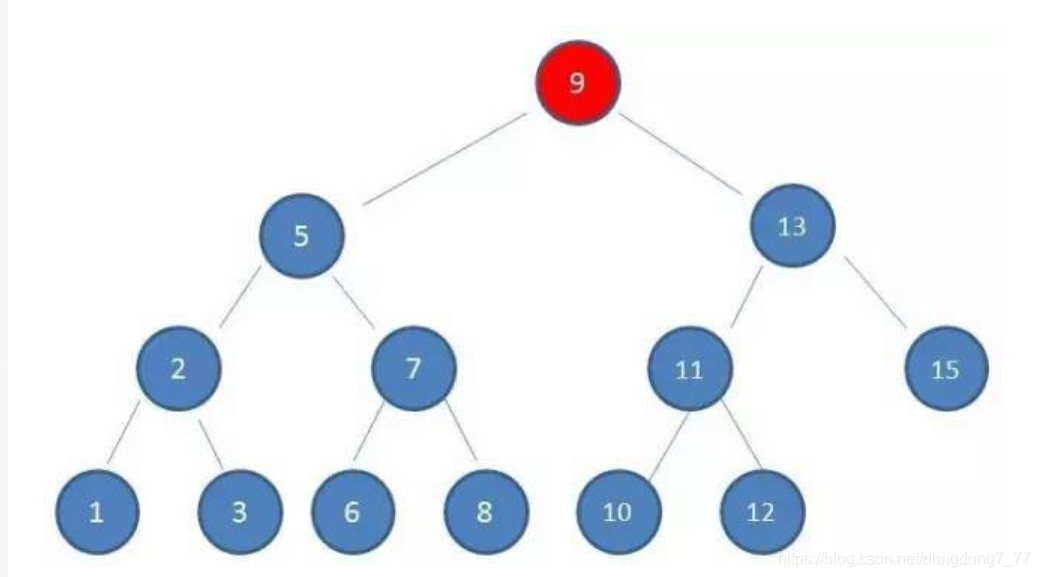
他有着以下特点

1. 左子树的上的值永远小于或等于右子树上的数
2. 右子树上的值永远大于左子树上的值
3. 左右子树同样也是一颗二叉查找树
   但是，问题来的，在一些特殊情况下会出现下图的状况，他的结构接近链表，时间复杂度接近O（n），
   

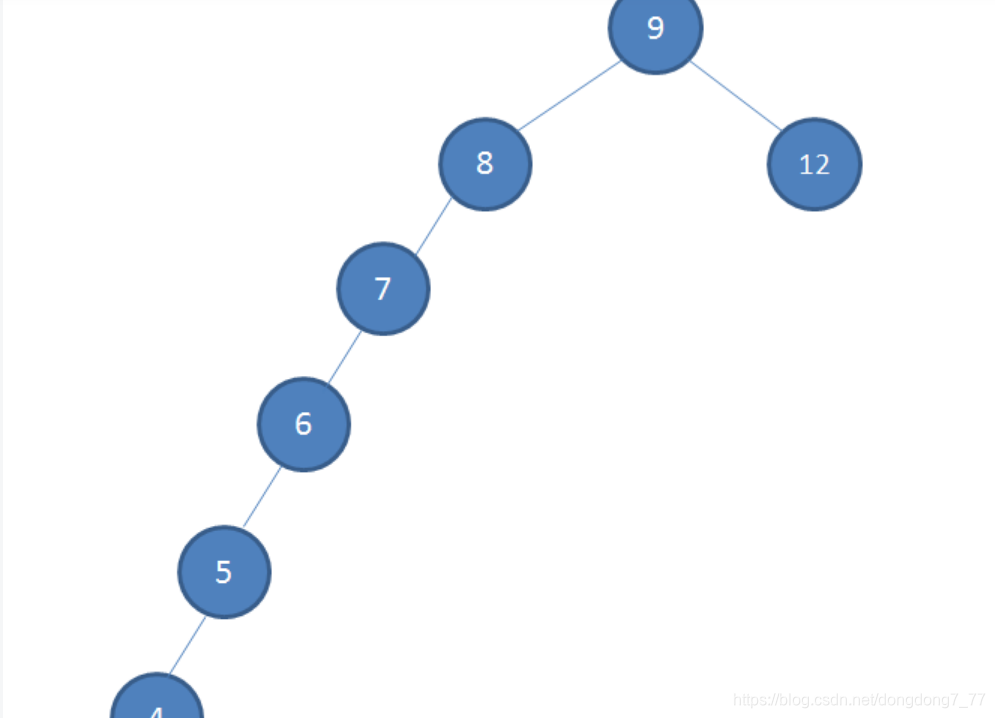
红黑树

怎么样上图的情况不会发生呢，我们引入了红黑树，我们先来看一下红黑树的特点

1. 每个结点不是红色就是黑色
2. 他的根结点是黑色
3. 不可能出现两个红色连接在一块的情况，但是两个黑色节点可以
4. 每个红色结点的两个结点都是黑色
   
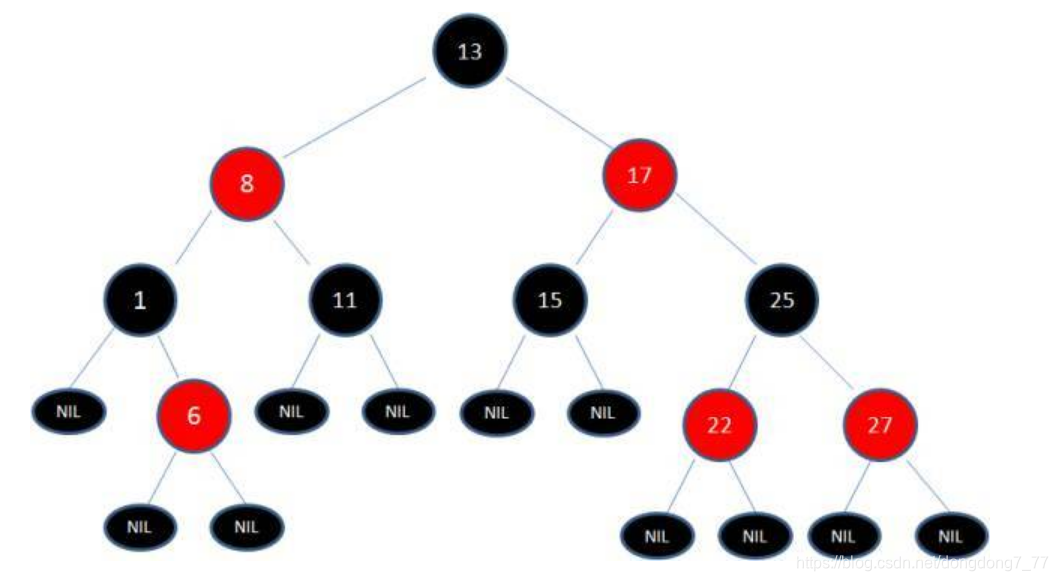
   但是当插入新的结点时，这种平衡就会被打破，所以我们需要一些操作来保证他的平衡——变色和旋转

变色和旋转

变色：就是把红色节点变为黑色，或者把黑色节点变为红色
旋转: 分为左旋和右旋

左旋：逆时针旋转红黑树的两个节点，使得父节点被自己的右孩子取代，而自己成为自己的左孩子

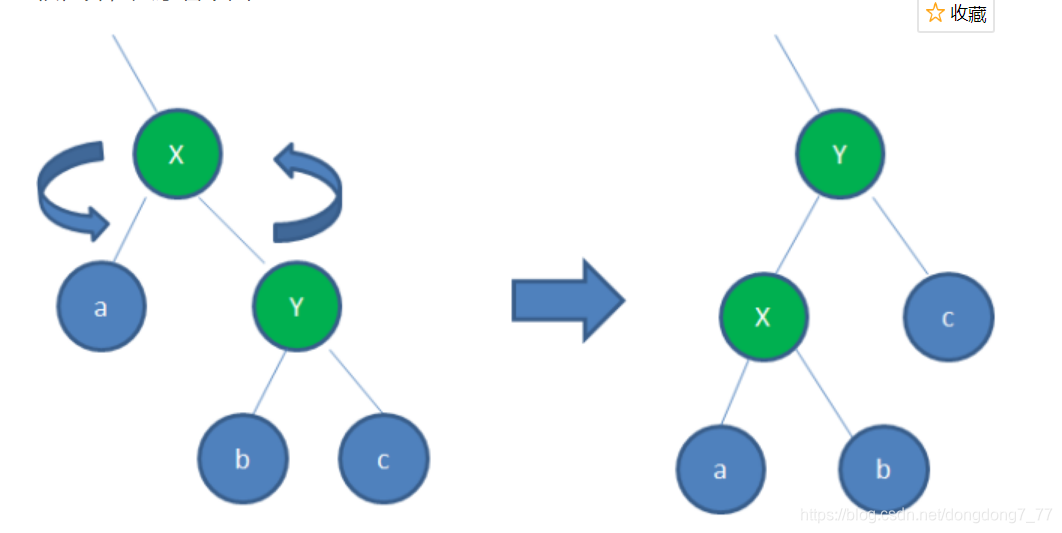
右旋： 顺时针旋转红黑树的两个节点，使得父节点被自己的左孩子取代，而自己成为自己的右孩子

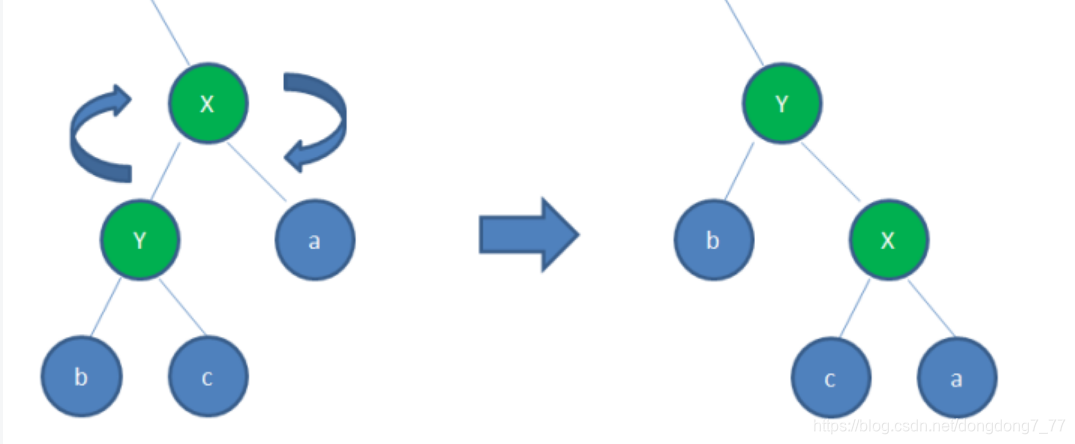
其中，红黑树的变色和旋转作是一个非常复杂的的过程，下来我们就来说一个常见的过程

1. 变色规则时插入的都为红色的结点
2. 变颜色的情况：当前结点的父亲时红色，且他的祖父结点的另一个结点也是红色（叔叔结点）
3. 把父亲结点变为黑色
4. 把父亲的结点的父亲结点变为红色色（爷爷结点）
5. 把指针定义到祖父结点设为当前要操作的变化的点
   左旋
6. 当前父节点时红色，叔叔结点是黑色的时候，且当前的结点是左子树。左旋以父节点作为左旋
   右旋
7. 当前父节点是红色，叔叔是黑色的时候，且当前结点是左子树，右旋
8. 把父节点变为黑色
9. 把祖父结点变为红色
   10.以祖父结点旋转