哈达玛变换及其在图像/视频编码中的应用：计算SATD

沃尔什-哈达玛变换（Walsh-Hadmard Transform,WHT），是一种典型的非正弦函数变换，采用正交直角函数作为基函数，具有与傅里叶函数类似的性质，图像数据越是均匀分布，经过沃尔什-哈达玛变换后的数据越是集中于矩阵的边角上，因此沃尔什变换具有能量集中的性质，把一个矩阵的非零元素压缩到只剩在边角上，可以用于压缩图像信息编码。哈达变换实际是将坐标轴旋转45°的正交变换。

哈达玛变换通常用于计算残差的SATD（Sum of Absolute Transformed Difference），即对残差信号进行哈达玛变换，然后计算变换后系数的绝对值的和。SATD相较于SAD更能反映残差在频域的大小。SATD通常用于率失真优化中，因为在率失真优化时如果对每个候选项都编码一遍然后计算失真则计算复杂度会非常高，所以一般使用残差的SATD估计其失真。

一阶二阶哈达玛矩阵定义为

 高阶哈达玛矩阵可由低阶的递推得到

哈达玛变换WHT就是使用哈达玛矩阵去乘原信号矩阵。

二维的WHT是要对原矩阵左乘一个对应阶的哈达玛矩阵，右边也乘一个，然后除以阶数平方即

 哈达玛变换结果可视化例如下

哈达玛变换优点

• 仅需实数运算 (Real operation) 。
• 不需乘法运算 (No multiplication) ，仅有加减法运算。
• 有部分性质类似于离散傅立叶变换 (Discrete fourier transform) 。
• 顺向转换 (Forward transform) 与反向转换 (Inverse transform ) 型式为相似式。

 

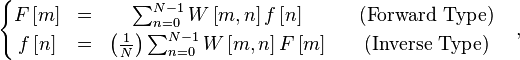
 哈达玛变换缺点

• 其收敛速度较离散余弦变换慢，因此对于频谱分析的效果较差。
• 其加减法量较离散傅立叶变换、离散余弦变换多。

用WHT逼近数字脉冲信号时比FFT有利，且WHT只需进行实数运算，存储量比FFT少的多，运算也快得多。在现在的视频编码标准中，哈达玛变换多被用来计算SATD(一种视频残差信号大小的衡量)。

x264的哈达玛变换(hadamard)的实现和优化

HEVC中哈达玛变换计算SATD的向量指令优化

转：X264中SATD实现分析 - Mr.Rico - 博客园

参考：

1. 数字图像处理 第7章_沃尔什-哈达玛变换 - 道客巴巴
2. 哈达玛变换 - 百度百科
3. 压缩感知——沃尔什-哈达玛(WHT)变换与逆变换的Matlab代码实现
4. Hadamard变换
5. H266VVC电子书开放下载啦_Dillon2015的博客-CSDN博客