数据结构——排序

作者：几冬雪来 

时间：2023年4月4日

内容：数据结构排序内容讲解

目录

前言： 

排序： 

1.插入排序： 

2.希尔排序： 

3.希尔排序gap问题：  

结尾： 

---

前言： 

在前不久我们结束了数据结构中二叉树板块的知识讲解，而今天我们就将开启数据结构新板块——排序的学习。

排序： 

排序作为我们数据结构的一个重要的知识板块，但其实在很久很久之前我们就已经接触过排序的知识了——冒泡排序，冒泡排序作为我们在C语言经常使用的一种将无序数组排列为有序数组的方法，它毫无疑问也是众多排序方法中的一份子，在今日我们将来我们的排序。 

1.插入排序： 

首先这里介绍的是我们的插入排序，插入排序在我们的日常生活中经常被使用到。经典的例子就类似我们的扑克牌，在摸完了第一张排之后，后面我们每摸上一张牌就要找一个合适的位置将它放入进去（没有整理牌习惯的人另当别论），这种就是我们典型的插入排序。 

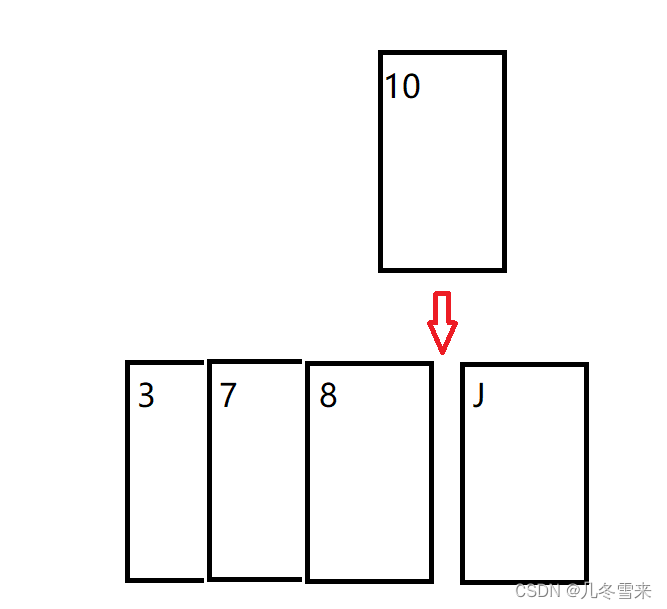
既然了解了插入排序大概的操作方法之后，接下来我们就要书写它的代码了，那么插入排序的代码是怎么写的呢？

这里我们就将它们插入排序的代码书写出来了，那么它是怎么样运行的呢？接下来我们就来对其进行讲解。 

首先我们要排序的是一个数组并非一个数，所以我们要写一个循环。与之前的i初始化为0不同，这里我们循环中的i初始化为1。循环一开始我们就将i-1赋值给end，同时将下标为1的结点的值赋值给tmp。接下来因为end为0满足条件所以进入我们的while循环，如果这里我们下标为1的结点的值小于下标为0的结点的值，这里我们就将下标为0的值赋值给下标为1处，然后end进行--操作，这个时候end为-1，不符合我们的循环条件，这里就不进入循环。最后我们将tmp也赋值给a[end+1]也就是下标为0处。

这里我们将它的图画出来。

同样的，如果我们的a[end]小于tmp的话，这里我们就直接跳出循环，将tmp的值给a[end+1]处即可。这个就是我们的插入排序。

而这里我们的插入排序的时间复杂度是多少呢？最坏的情况如果我们的数组是逆序的，这里我们的时间复杂度为O(N^2)，而最好的情况则是顺序且有序，时间复杂度为O(N)。

2.希尔排序： 

在讲解完了插入排序之后，接下来我们就来讲解的是我们排序板块中一个重要的排序方法——希尔排序。希尔排序也是一种插入排序，它又叫缩小增量插入排序。

在学习完了插入排序之后，我们可以得知，如果我们的数组越接近顺序有序的话，那么插入排序的时间复杂度会很小，如果接近于无序（逆序）的话，那么插入排序的时间复杂度会很大。

而这里希尔排序则对其进行了一步优化。

这里就是我们优化后的操作，在进行插入排序之前我们先对其进行预排序的操作，使数组更快的从无序变为有序。 

而这里我们的预排序则是使用的分组插排的方法。而且这里的分组插排实际上的操作就是将间隔为gap的值分为一组，对每组数据进入插入排序。这里我们画一张图来演示一下，假设我们的gap的值为3：

虽然在进行完了一次分组插排之后，我们的数组依旧是无序的，但是先比较与未进行分组排序的数组，这里的它更加接近于有序。而这种方法的优势在于，如果类似上面这个图，如果我们单纯的进行插入排序的话，作为数组头元素的9如果要到数组的最后边的话，这里要跳n-1次才能到达。但是如果是分组插排的话，这里的9要到最后一个位置的话，我们只需要跳动3次。

这里我们也将它的代码写出来，因为我们说过希尔排序也是一种插入排序，因此希尔排序（单趟）的代码只需要将插入排序的代码稍微修改即可。

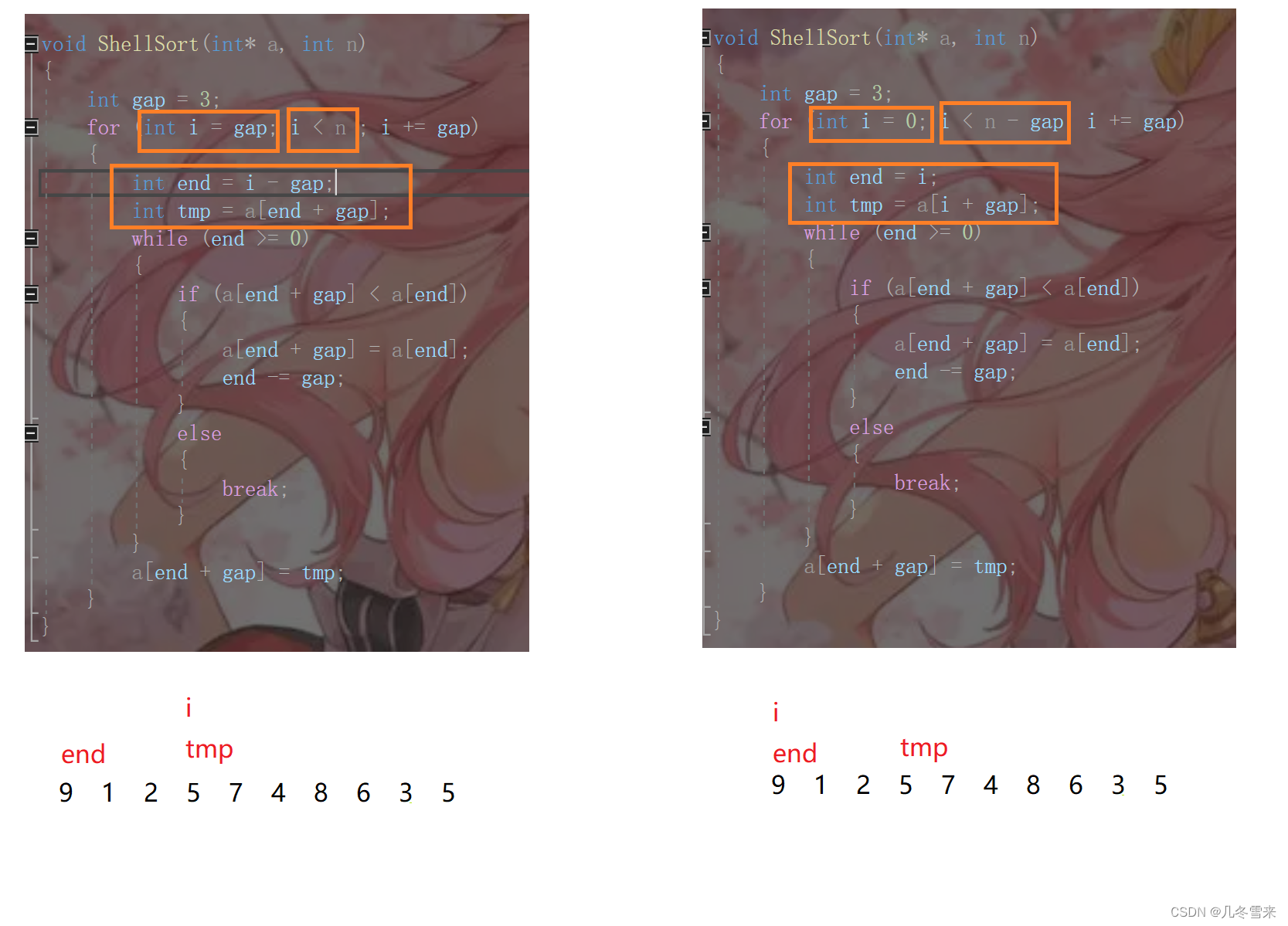
这里就是我们希尔排序单趟排序的代码。这里的实验理论可以直接套用插入排序的理论，我就不再写一遍了，并且它的代码有两种书写形式，一个是i在end处，一个是tmp处，同时我们的循环条件也会有所不同，如果是后面这组代码我们i循环终止的条件是i<n-gap，这个时候tmp刚刚好在数组最后的5处，如果像第一种方法判断条件为i<n的话，这里我们的tmp就会越界。 

这里是我们单趟的代码，因为gap将我们的代码分为了3组，这里我们需要走3次。

这里解决问题的方法就是在我们原先代码的基础上再套一层循环。每次j++之后，它就到我们下一组数组的头元素。

但是这里的解决方法并不止一种，我们也可以不再套一层循环就能实现我们的代码，那么这种方法的代码又应该怎么书写的呢？

在这里我们将i初始化为0，i的调整改为i++就行了。那么这里是怎么实现的呢？我们再画一个图来表达看看。

在这里一开始的时候，是对第一组数组的一个下标为end和下标为i+gap的值进行一个调换，i++后到达下一组数组，再让它的下标为end和下标为i+gap的值进行一个调换，与上面调换结束一组之后在调换另一组的方法不同，这里我们是先调换一次第一组的两个值，接下来再调换第二组的两个值，当3组都走过了一次之后，接下来我们再对第一组进行第二次的调换。

这里我们将代码进行运作。

从结果来看，这里我们的代码虽然相较于原版更接近顺序升序，但是实际上它还并不是有序的，这是为什么呢？这里就要涉及我们gap的问题了。

3.希尔排序gap问题：  

由上面可知，当gap为3这个固定值的时候，我们只是把数组中的间隔为3的值进行了排序。但是也是仅此而已，这里因为gap为固定的值，所以我们的操作仅仅是对代码进行了预排序而已。想要真正的让代码变得有序，理论上我们得再写一个gap为1的代码，但是这样操作的话未免太麻烦了，那么这里我们要怎么设计gap比较合适呢？

 

通过上面这句话，我们可以得出一个结论，在希尔排序之中，gap是变化的。 

而这里的第一种方法就类似我们下图。

一开始gap的值为n，每进行一次循环（条件为gap大于1）gap就除等于2，那么在执行多次循环之后，这里的gap最后会变为1，也就是变成一个单纯的插入排序。 

  

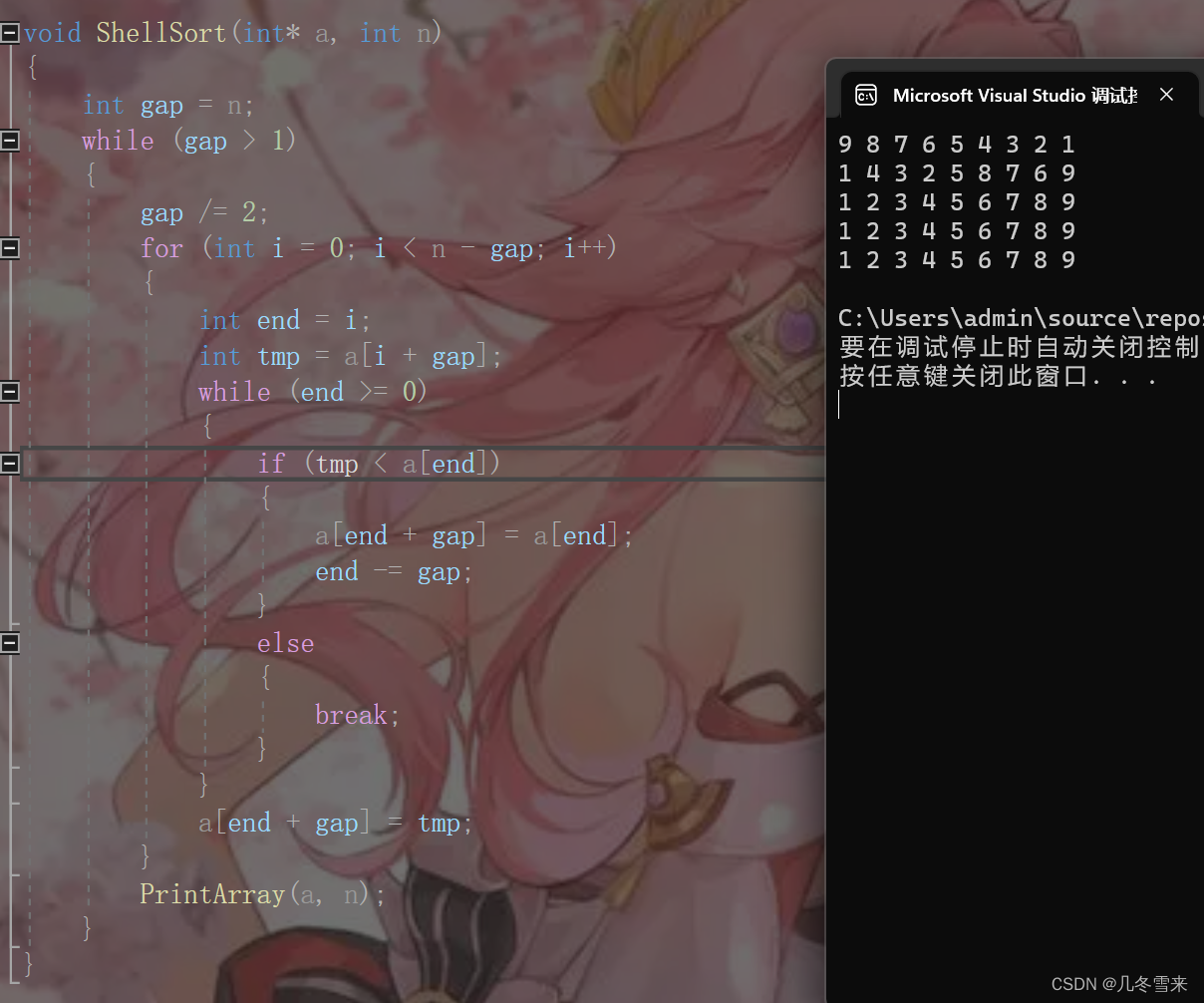
这里就刚刚好完成了我们的排序。又因为在希尔排序中，它并没有规定我们的gap的值，因此在这里我们的gap的值也可以写成。 

 

这里的+1是为了保证最后一次gap的值为1，这两种写法都是可以的。这里我们也总结出来了一个结论。

 

这就是希尔排序的操作。

结尾： 

到这里，我们希尔排序的代码就已经写好了，在后面我们还会讲解一下希尔排序的时间复杂度，并且在更后面的地方还有更难的排序在等着我们去解决。最后这里希望这篇博客可以给大家带来帮助。