前文:很久没有写博客了呢 ,一直没有时间(在浪)
题意不提。
最后要求的式子
我们单独看这坨cegma
我们可以在o(n)的时间筛出phi(d)。
总复杂度o(n)
代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<cctype>
#include<string>
#include<cstring>
const int N = 1e5 + 7;
int n, m, prime[N], p, phi[N];
long long ans;
bool c[N];
int main () {
scanf ("%d%d", &n, &m);
if (n > m) n ^= m ^= n ^= m;
phi[1] = 1;
for (int i = 2; i <= n; ++i) {
if (!c[i]) prime[++p] = i, phi[i] = i - 1;
for (int j = 1; j <= p && (long long) i * prime[j] <= n; ++j) {
c[i * prime[j]] = true;
if (i % prime[j] == 0) {
phi[i * prime[j]] = phi[i] * prime[j];
break;
} else {
phi[i * prime[j]] = phi[i] * (prime[j] - 1);
}
}
}
for (int i = 1; i <= n; ++i) {
ans += (long long) (n / i) * (m / i) * phi[i];
}
printf ("%lld\n", ans * 2 - (long long) n * m);
return 0;
}










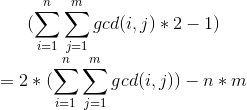















 991
991

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








