数据结构–创建并输出二叉树的c语言实现(超详细注释/实验报告)
知识小回顾
之前我们都是学习的线性结构,这次我们就开始学习非线性结构——树。线性结构中结点间具有唯一前驱、唯一后继关系,而非线性结构中结点的前驱、后继的关系并不具有唯一性。在树结构中,节点间关系是前驱唯一而后继不唯一,即结点之间是一对多的关系。直观地看,树结构是具有分支关系的结构(其分叉、分层的特征类似于自然界中的树)。树结构应用非常广泛,特别是在大量数据处理(如在文件系统、编译系统、目录组织等)方面显得更加突出。
实验题目
创建并输出二叉树
实验目的
- 熟悉二叉树的结点的结构
- 采用链式存储表示
- 以广义表形式输入二叉树
- 使用栈保存尔察使书的根结点
- 输出方式采用凹入表示法
实验要求
- 采用链式存储表示
- 以广义表形式输入二叉树
- 使用栈保存尔察使书的根结点
- 输出方式采用凹入表示法
实验内容和实验步骤
1.需求分析
用户输入二叉树的广义表形式,程序输出二叉树
2. 概要设计
设计创建和输出二叉树的函数,然后再主函数中调用这两个函数来实现操作。
3. 详细设计
导入一些库,并定义结点的最大个数以及树中数据的类型。
- 定义二叉树的链式存储结构,有三个域:数据域,左孩子域,右孩子域
#include<stdio.h>
#include<stdlib.h>
#define MAXSIZE 255
//定义二叉树的链式存储结构,有三个域:数据域,左孩子域,右孩子域
typedef struct BiNode
{
char data;
struct BiNode *lc;
struct BiNode *rc;
}BiTree;
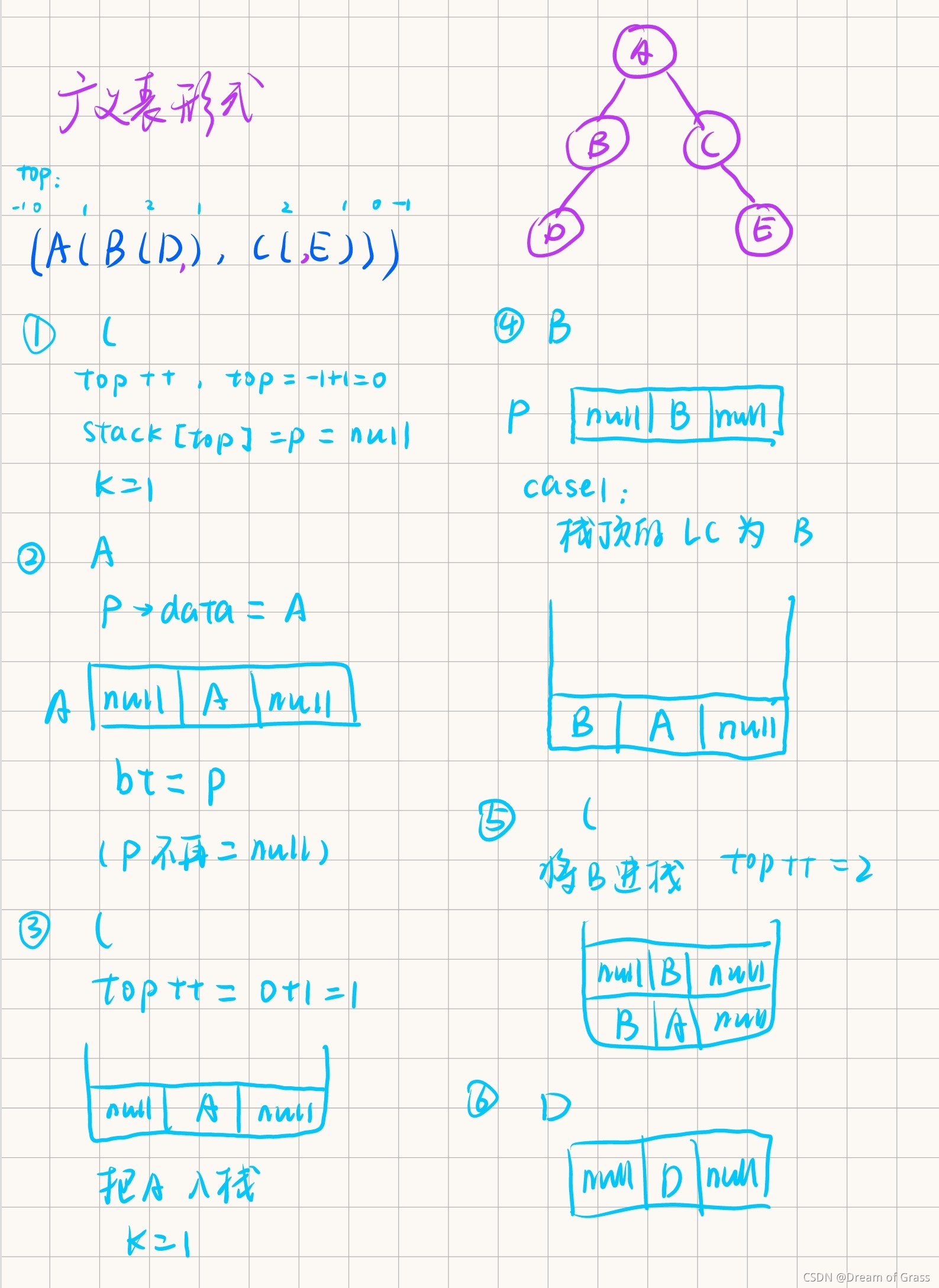
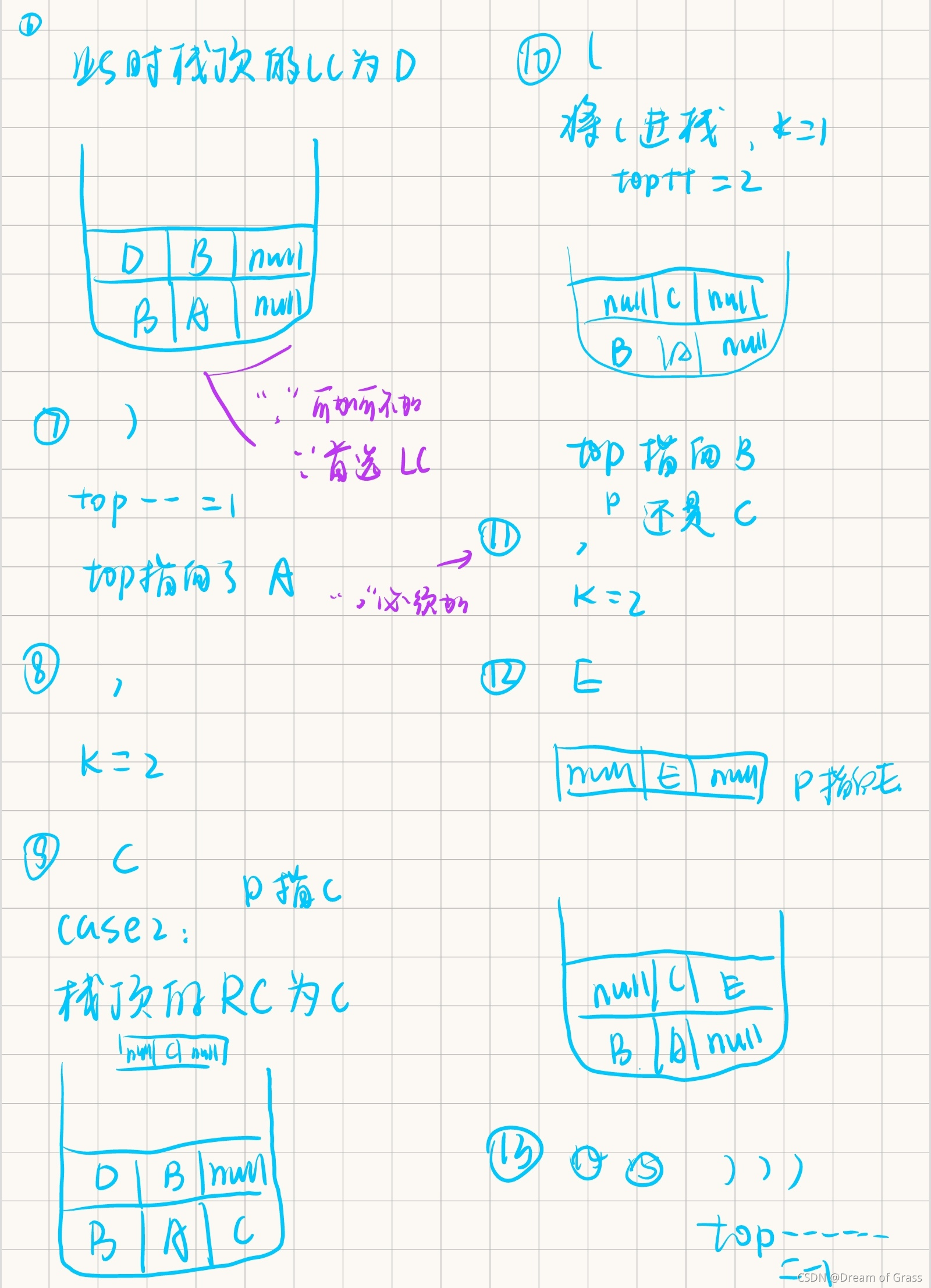
以广义表的形式创建二叉树
- 算法比较复杂,我画了个流程图,跟着这个图可以比较清晰地理解算法。
- 由于是链式存储,最后只用返回一个根节点bt就行了,其他结点直接顺藤摸瓜即可。
//以广义表的形式创建二叉树
BiTree *CreatBiTreepre(char *str)
{
BiTree *bt,*stack[MAXSIZE],*p=NULL;
int top=-1,k,j=0;
char ch;
bt=NULL;
ch=str[j];
while(ch!='\0')
{
switch(ch)
{
case '(':
{
top++;
stack[top]=p;
k=1;
break;
}
case ')':
{
top--;
break;
}
case ',':
{
k=2;
break;
}
default:
{
p=(BiTree *)malloc(sizeof(BiTree));
p->data=ch;
p->lc=p->rc=NULL;
if(bt==NULL)
{
bt=p;
}
else
{
switch(k)
{
case 1:
{
stack[top]->lc=p;
break;
}
case 2:
{
stack[top]->rc=p;
break;
}
}
}
}
}
j++;
ch=str[j];
}
return bt;//链式存储只用知道一个,后面顺藤摸瓜就都知道了
}
采用凹入法输出二叉树
- 算法同样比较复杂,也是跟着流程图来~
//采用凹入法输出二叉树
void OutBiTree(BiTree *bt)
{
BiTree *stack[MAXSIZE],*p;
int feature[MAXSIZE][2],top,n,i,width=4;
char type;
if(bt!=NULL)
{
top=1;
stack[top]=bt;
feature[top][0]=width;
feature[top][1]=2;
while(top>0)
{
p=stack[top];
n=feature[top][0];
switch(feature[top][1])
{
case 0:
{
type='l';
break;
}
case 1:
{
type='R';
break;
}
case 2:
{
type='G';
break;
}
}
for(i=1;i<=n;i++)
printf(" ");
printf("%c(%c)\n",p->data,type);
top--;
if(p->lc!=NULL)
{
top++;
stack[top]=p->lc;
feature[top][0]=n+width;
feature[top][1]=0;
}
if(p->rc!=NULL)
{
top++;
stack[top]=p->rc;
feature[top][0]=n+width;
feature[top][1]=1;
}
}
}
}

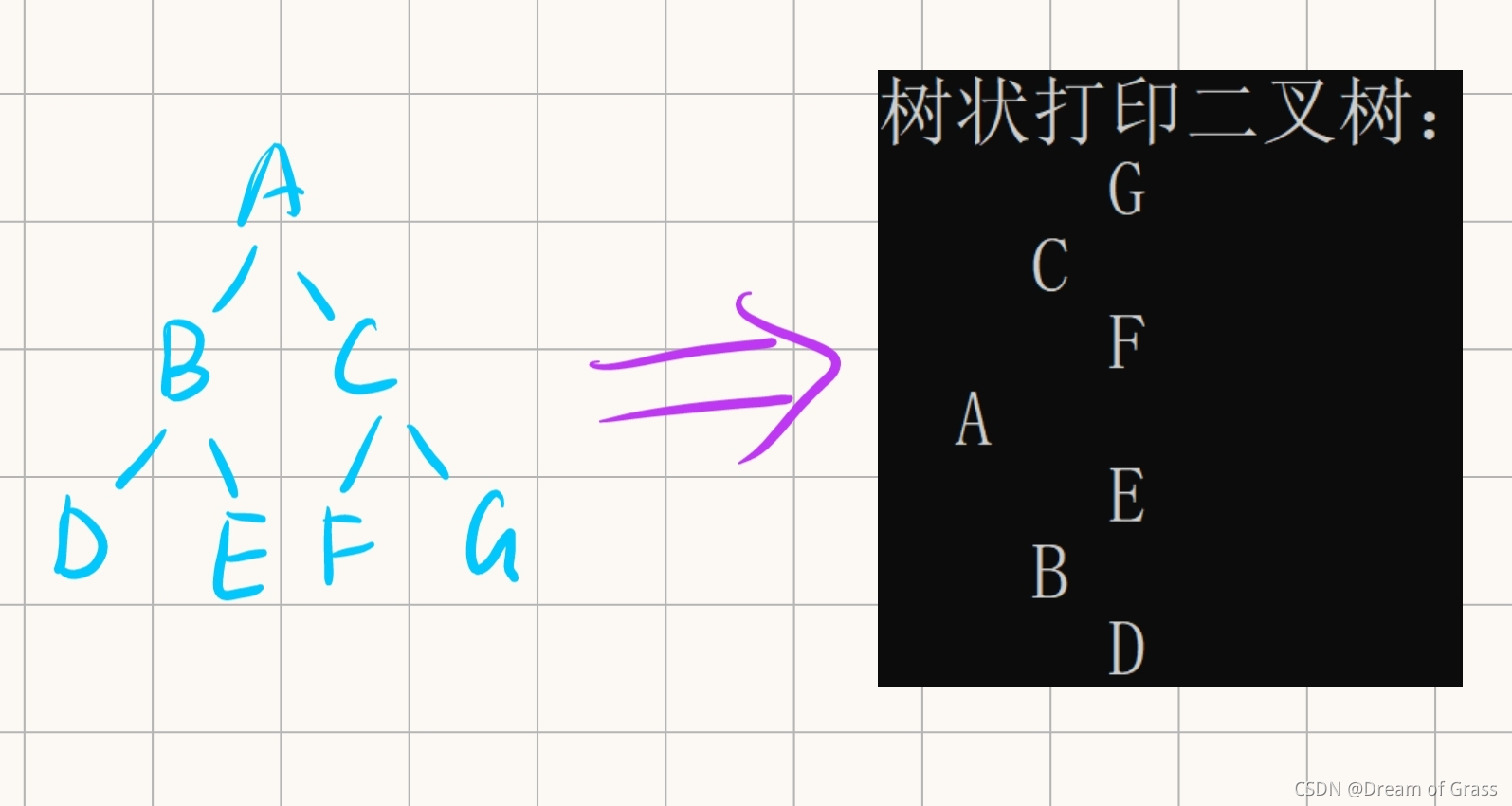
树状打印二叉树
- 二叉树的横向显示是竖向显示逆时针旋转90°。
void PrintTree(BiTree *bt,int nLayer)
{
if(bt==NULL)
return ;
PrintTree(bt->rc,nLayer+1);
for(int i=0;i<nLayer;i++)
printf(" ");
printf("%c\n",bt->data);
PrintTree(bt->lc,nLayer+1);
}
主函数部分,把程序功能打印出来,并对用户做一个引导。

int main()//(A(B(D,),C(,E))) (A(B(D,E),C(F,G))) ((((A),B)),(((),D),(E,F)))这个不是树
{
BiTree *bt;
char *gyb,str[MAXSIZE];
int j=1;
printf("-----------------------------------------------------");
printf("\n 程序功能");
printf("\n 1.将按照输入的二叉广义表表示字符串 ");
printf("\n · 生成对应的二叉树链式结构。");
printf("\n 2.输出二叉树的凹入法表示形式。");
printf("\n · G--根 L--左孩子 R--右孩子");
printf("\n 3.树状打印二叉树");
printf("\n · 逆时针旋转90度显示二叉树");
printf("\n * 输入示例:(A(B(D,),C(,E)))或(A(B(D,E),C(F,G)))");
printf("\n-----------------------------------------------------\n");
printf("请输入二叉树的广义表形式:\n");
gyb=str;
scanf("%s",str);
bt =CreatBiTreepre(gyb);
printf("二叉树建立成功!\n");
printf("此二叉树的凹入法表示为:\n");
OutBiTree(bt);
printf("树状打印二叉树:\n");
PrintTree(bt,1);
return 0;
}
4. 调试分析
遇到的问题及解决方法
- 算法思想比较复杂,通过举例子、一步一步画图拨开了云雾。
算法的时空分析
这里只有分支结构,没有循环结构,所以时间复杂度很低。同时也采取了链式存储,空间复杂度也不大。
实验结果
实验结果很不错,所有操作都能正常执行,并且自己加入了按树状打印二叉树,使得输出效果更加美观。
这是上面分析的例子的程序给出的输出。

下面这个例子大家也可以看看。


实验总结
比较复杂,但只要认真分析就没事,多多重复,百炼成钢!
最后附上完整的代码
#include<stdio.h>
#include<stdlib.h>
#define MAXSIZE 255
//定义二叉树的链式存储结构,有三个域:数据域,左孩子域,右孩子域
typedef struct BiNode
{
char data;
struct BiNode *lc;
struct BiNode *rc;
}BiTree;
//以广义表的形式创建二叉树
BiTree *CreatBiTreepre(char *str)
{
BiTree *bt,*stack[MAXSIZE],*p=NULL;
int top=-1,k,j=0;
char ch;
bt=NULL;
ch=str[j];
while(ch!='\0')
{
switch(ch)
{
case '(':
{
top++;
stack[top]=p;
k=1;
break;
}
case ')':
{
top--;
break;
}
case ',':
{
k=2;
break;
}
default:
{
p=(BiTree *)malloc(sizeof(BiTree));
p->data=ch;
p->lc=p->rc=NULL;
if(bt==NULL)
{
bt=p;
}
else
{
switch(k)
{
case 1:
{
stack[top]->lc=p;
break;
}
case 2:
{
stack[top]->rc=p;
break;
}
}
}
}
}
j++;
ch=str[j];
}
return bt;//链式存储只用知道一个,后面顺藤摸瓜就都知道了
}
//采用凹入法输出二叉树
void OutBiTree(BiTree *bt)
{
BiTree *stack[MAXSIZE],*p;
int feature[MAXSIZE][2],top,n,i,width=4;
char type;
if(bt!=NULL)
{
top=1;
stack[top]=bt;
feature[top][0]=width;
feature[top][1]=2;
while(top>0)
{
p=stack[top];
n=feature[top][0];
switch(feature[top][1])
{
case 0:
{
type='l';
break;
}
case 1:
{
type='R';
break;
}
case 2:
{
type='G';
break;
}
}
for(i=1;i<=n;i++)
printf(" ");
printf("%c(%c)\n",p->data,type);
top--;
if(p->lc!=NULL)
{
top++;
stack[top]=p->lc;
feature[top][0]=n+width;
feature[top][1]=0;
}
if(p->rc!=NULL)
{
top++;
stack[top]=p->rc;
feature[top][0]=n+width;
feature[top][1]=1;
}
}
}
}
void PrintTree(BiTree *bt,int nLayer)
{
if(bt==NULL)
return ;
PrintTree(bt->rc,nLayer+1);
for(int i=0;i<nLayer;i++)
printf(" ");
printf("%c\n",bt->data);
PrintTree(bt->lc,nLayer+1);
}
int main()//(A(B(D,),C(,E))) (A(B(D,E),C(F,G))) ((((A),B)),(((),D),(E,F)))这个不是树
{
BiTree *bt;
char *gyb,str[MAXSIZE];
int j=1;
printf("-----------------------------------------------------");
printf("\n 程序功能");
printf("\n 1.将按照输入的二叉广义表表示字符串 ");
printf("\n · 生成对应的二叉树链式结构。");
printf("\n 2.输出二叉树的凹入法表示形式。");
printf("\n · G--根 L--左孩子 R--右孩子");
printf("\n 3.树状打印二叉树");
printf("\n · 逆时针旋转90度显示二叉树");
printf("\n * 输入示例:(A(B(D,),C(,E)))或(A(B(D,E),C(F,G)))");
printf("\n-----------------------------------------------------\n");
printf("请输入二叉树的广义表形式:\n");
gyb=str;
scanf("%s",str);
bt =CreatBiTreepre(gyb);
printf("二叉树建立成功!\n");
printf("此二叉树的凹入法表示为:\n");
OutBiTree(bt);
printf("树状打印二叉树:\n");
PrintTree(bt,1);
return 0;
}
























 1215
1215

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








