主成分分析（Principle Component Analysis）

主成分分析（Principle Component Analysis, PCA）是一种特征提取的方法，设 { X i } ， i = 1 ∼ p \{X_i\}，i=1\sim p {Xi​}，i=1∼p 是一组样本的输入，其中$X_i=(x_{i1},x_{i2},\cdots ,x_{in}{)}^T$，PCA的目的是构造一个线性变换 $Y=AX+b$ 把 $n$ 维特征 $X$ 转成 $m$ 维特征 $Y$，实现数据的降维（$n>m$），每个量的维度为：

parameter	shape
$Y$	$(m,1)$
$A$	$(m,n)$
$X$	$(n,1)$
$b$	$(m,1)$

PCA可以看成是只一层的有$m$个神经元的神经网络：

自编码器（Auto-encoder）的思想也是对标PCA的：

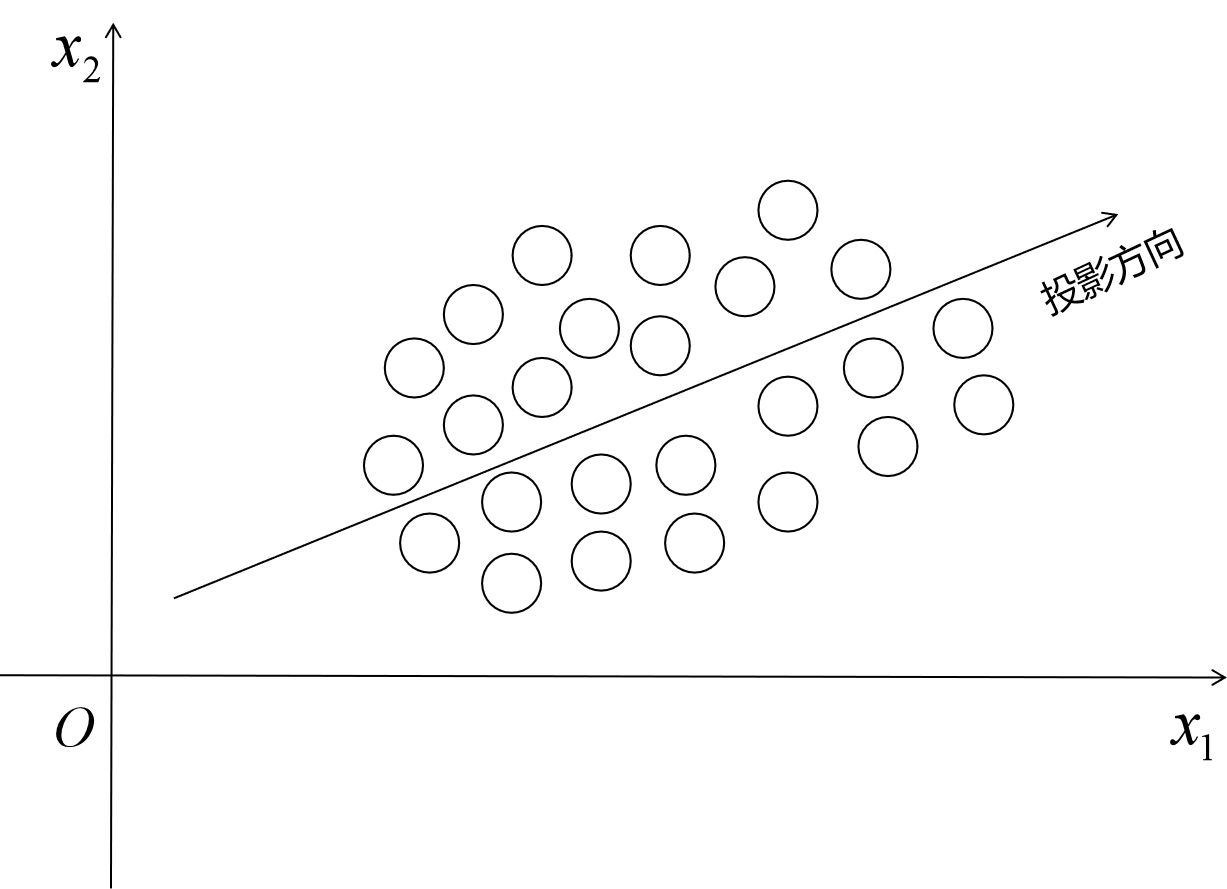
直观来说，PCA的目标是寻找方差最大方向，并在该方向投影，例如取$n=2,m=1$，则每个数据有2个维度的特征 $x=(x_1,x_2{)}^T$，将其投影到一个维度上，使数据在该维度上方差最大，这个方向就是 $y=y_1$ 如下图所示：

---

下面对PCA进行推导

设数据集为 { X i } , i = 1 ∼ p \{X_i\},i=1\sim p {Xi​},i=1∼p，我们采用如下线性变换来进行PCA：$$\begin{array}{r}\{\begin{array}{l}Y=A(X-\overline{X})\\ \\ \overline{X}=E(X)=\frac{1}{p}\sum _{i=1}^p{X}_i\end{array}\end{array}$$为了方便计算，设$A=\left(\begin{array}{c}{a}_1\\ a_2\\ ⋮\\ a_m\end{array}\right)$，其中$a_i=(a_{i1},a_{i2},\cdots ,a_{in})，i=1\sim m$，代入线性变换可得：$$Y_i=\left(\begin{array}{c}{a}_1(X_i-\overline{X})\\ a_2(X_i-\overline{X})\\ ⋮\\ a_m(X_i-\overline{X})\end{array}\right)=\left(\begin{array}{c}{y}_{i1}\\ y_{i2}\\ ⋮\\ y_{im}\end{array}\right),i=1\sim p(y_{ij}是1\times 1的矩阵也就是数)$$我们已经说过，PCA是为了找到数据方差最大的$m$个方向进行投影，所以我们的目标函数就是最大化 $Y_i$ 每个维度上数据的方差，即最大化数据序列 { y i j } \{y_{ij}\} {yij​}的方差，其中$i=1\sim p,j=1\sim m$，以 { y i 1 } \{y_{i1}\} {yi1​}为例,最大化的目标函数是：
$$\begin{array}{rl}& \sum _{i=1}^p(y_{i1}-\overline{y_{i1}}{)}^2\\ =& \sum _{i=1}^p{y}_{i1}^2\\ =& \sum _{i=1}^p[a_1(X_i-\overline{X}){]}^2\\ =& \sum _{i=1}^p{a}_1(X_i-\overline{X})(X_i-\overline{X}{)}^T{a}_1^T\\ =& a_1[\sum _{i=1}^p(X_i-\overline{X})(X_i-\overline{X}{)}^T]a_1^T\\ =& a_i\sum a_1^T\end{array}$$其中$\sum =\sum _{i=1}^p(X_i-\overline{X})(X_i-\overline{X}{)}^T$称为协方差矩阵（covariance matrix），显然$\sum ={\sum }^T$是对称矩阵，其维度为 $n\times n$

为什么 $\overline{y_{i1}}=0$？
$$\begin{array}{rl}\overline{y_{i1}}=& \frac{1}{p}\sum _{i=1}^p{y}_{i1}=\frac{1}{p}\sum _{i=1}^p{a}_1(X_i-\overline{X})\\ =& \frac{a_1}{p}\sum _{i=1}^p(X_i-\overline{X})=\frac{a_1}{p}(\sum _{i=1}^p{X}_i-\sum _{i=1}^p\overline{X})\\ =& \frac{a_1}{p}(\sum _{i=1}^p{X}_i-p\overline{X})=\frac{a_1}{p}\times \mathbf{O}\\ =& 0\end{array}$$这里要记得 $\overline{X}=\frac{1}{p}\sum _{i=1}^p{X}_i$

此时还有个问题，$a_1$ 虽然确定了方向，但是 $a_1$ 的模的大小未定，如果 $||a_1||$ 越大，则投影越大，所以要对 $||a_1||$ 进行限制，至此，我们的问题就变成了这样：
$$\begin{array}{rl}& \max a_1\sum a_1^T\\ & s.t.a_1{a}_1^T=||a_1|{|}^2=1\end{array}$$我们可以用拉格朗日乘数法求解：
$$\begin{array}{rl}目标函数为& L(a_1,\alpha )=a_1\sum a_1^T-\alpha (a_1{a}_1^T-1)\\ & \\ & \frac{\partial L}{\partial a_1}=2a_1\sum -2\alpha a_1=0⟹{\sum }^T{a}_1^T=\sum a_1^T=\alpha a_1^T\\ & \\ 所以& \alpha 是\sum 的特征值，对应特征向量为a_1^T\\ & \\ ⟹& a_1\sum a_1^T=a_1\alpha a_1^T=\alpha \\ & \\ 由于要& 最大化方差，所以\alpha 应该是\sum 的最大的特征值，记为{\lambda }_1，则a_1^T就是对应于{\lambda }_1的单位特征向量\end{array}$$

拉格朗日乘数法计算过程
设$a_1=(a_{11},a_{12},\cdots ,a_{1n})$, $a_1^T=\left(\begin{array}{c}{a}_{11}\\ a_{12}\\ ⋮\\ a_{1n}\end{array}\right)$，$\sum =\left(\begin{array}{cccc}{\sigma }_{11}& {\sigma }_{12}& \cdots & {\sigma }_{1n}\\ {\sigma }_{21}& {\sigma }_{22}& \cdots & {\sigma }_{2n}\\ ⋮& ⋮& & ⋮\\ {\sigma }_{n1}& {\sigma }_{n2}& \cdots & {\sigma }_{nn}\end{array}\right)$，则：
$$\begin{array}{rl}& \{\begin{array}{l}{a}_1\sum =(\sum _{i=1}^n{a}_{1i}{\sigma }_{i1},\sum _{i=1}^n{a}_{2i}{\sigma }_{i2},\cdots ,\sum _{i=1}^n{a}_{ni}{\sigma }_{in})\\ a_1\sum a_1^T=a_{11}\sum _{i=1}^n{a}_{1i}{\sigma }_{i1}+a_{12}\sum _{i=1}^n{a}_{2i}{\sigma }_{i2}+\cdots +a_{1n}\sum _{i=1}^n{a}_{ni}{\sigma }_{in}\end{array}\\ ⟹& \frac{\partial (a_1\sum a_1^T)}{\partial a_{1k}}=\sum _{i=1}^n{a}_{1i}{\sigma }_{ki}+\sum _{i=1}^n{a}_{1i}{\sigma }_{ik}，又\sum ={\sum }^T⟹{\sigma }_{ij}=\sigma ji\\ ⟹& \frac{\partial (a_1\sum a_1^T)}{\partial a_{1k}}=2\sum _{i=1}^n{a}_{1i}{\sigma }_{ik}=2a_1\left(\begin{array}{c}{\sigma }_{1k}\\ {\sigma }_{2k}\\ ⋮\\ {\sigma }_{nk}\end{array}\right)(k=1\sim n)\\ ⟹& \frac{\partial (a_1\sum a_1^T)}{\partial a_1}=(\frac{\partial (a_1\sum a_1^T)}{\partial a_{11}},\frac{\partial (a_1\sum a_1^T)}{\partial a_{12}},\cdots ,\frac{\partial (a_1\sum a_1^T)}{\partial a_{1n}})=2a_1\sum \\ & \\ & a_1{a}_1^T=\sum _{i=1}^n{a}_{1i}^2\\ ⟹& \frac{\partial a_1{a}_1^T}{\partial a_{1k}}=2a_{1k}(k=1\sim n)\\ ⟹& \frac{\partial a_1{a}_1^T}{\partial a_1}=2a_1\end{array}$$

下面再来看看如何寻找第二个维度的最大方差，此时要把 { y i 1 } \{y_{i1}\} {yi1​}换成 { y i 2 } \{y_{i2}\} {yi2​}，和上面推导类似，就简化写了：

这里注意，限制条件多了一个正交条件，因为已经确定了最大方差的一个方向，现在要找一个除了它以外最大方差的方向，故要保证正交，找第三、第四等方向类似，都要与已经找到的方向正交.

$$\begin{array}{rl}max& \sum _{i=1}^p(y_{i2}-\overline{y_{i2}}{)}^2=a_2\sum a_2^T\\ & \\ s.t.& a_2{a}_2^T=||a_2|{|}^2=1\\ & \\ & a_1{a}_2^T=a_2{a}_1^T=0\\ & \\ 目标函数& L(a_2,\alpha ,\beta )=a_2\sum a_2^T-\alpha (a_2{a}_2^T-1)-\beta a_1{a}_2^T\\ & \\ & \frac{\partial L}{\partial a_2}=2a_2\sum -2\alpha a_2-\beta a_1=0\\ & \\ ⟹& 2a_2\sum a_1^T-2\alpha a_2{a}_1^T-\beta a_1{a}_1^T=0\\ & \\ ⟹& 2a_2{\lambda }_1{a}_1^T-\beta =0\\ & \\ ⟹& \beta =0\\ & \\ ⟹& \frac{\partial L}{\partial a_2}=2a_2\sum -2\alpha a_2=0\\ & \\ ⟹& \sum a_2^T=\alpha a_2^T\\ & \\ 所以\alpha 应该& 是\sum 的除{\lambda }_1以外最大的特征值，记为{\lambda }_2，则a_2^T就是对应于{\lambda }_2的单位特征向量\end{array}$$

---

PCA算法

1. 求$\sum =\sum _{i=1}^p(X_i-\overline{X})(X_i-\overline{X}{)}^T$
2. 求$\sum$的特征值 ${\lambda }_i$ 及其对应的单位特征向量 $a_i^T$ ，其中${\lambda }_{i-1}\ge {\lambda }_i$
3. 写出矩阵 $A=\left(\begin{array}{c}{a}_1\\ a_2\\ ⋮\\ a_m\end{array}\right)$
4. 降维：$Y_i=A(X_i-\overline{X}),i=1\sim p$

【注】
        实际使用中，由于$X$的每个维度数据的量纲可能不同，直接拿来用PCA可能会导致结果错误，故最好先Normalization，使均值为 $0$，方差为 $1$

如何选择 $k$ 个主成分

第 $k$ 个主成分 $y_k$ 的方差贡献率定义为 $y_k$ 的方差与所有方差之和的比，记作 ${\eta }_k$：$${\eta }_k=\frac{{\lambda }_k}{\sum _{i=1}^m{\lambda }_i}$$$k$个主成分$y_1,y_2,\cdots ,y_k$的累计方差贡献率定义为 $k$ 个方差之和与所有方差之和的比：$$\sum _{i=1}^k{\eta }_i=\frac{\sum _{i=1}^k{\lambda }_i}{\sum _{i=1}^m{\lambda }_i}$$
通常取 $k$ 使得累计方差贡献率达到规定的百分比以上，例如达到 $90\%$ 以上。