目录
在多核系统中，衡量程序性能的一个重要指标就是加速比，加速比定义如下：
S(n) ＝ 单处理器上最优串行化算法计算时间 / 使用n个处理器并行计算时间
众所周知，关于加速比有一个阿姆达尔定律，说的是加速比方面的事情，即加速比S(n)
和串行部分所占比例f
有关，而与CPU
核数n
无关，也就是说
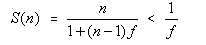
当处理器个数n
趋近于无穷大时，有以下等式。
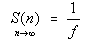
阿姆达尔定律的提出让整个软件界灰心了许多年，因为只要串行比例为5
％，那么不论增加多少处理器，加速比最多也只能达到20
。
若干年后一个叫Gustafson
的人提出了和阿姆达尔定律不同的意见，得到了一个新的加速比公式如下：
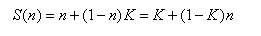
其中的K
是一个常数，表示串行执行时间所占的比例。
按照Gustafson
定律，加速比显然和CPU
核数n
是成正比的，CPU
核数越大，加速比也越大。
Gustafson
定律的前提条件假设串行化代码的规模是固定的，计算规模是随CPU
核数增加而增加的。实际情况中，共享资源访问的计算量和程序的计算规模是成正比的，如果共享资源通过锁保护操作而变成串行化执行的话，那么串行化代码的规模将随程序规模的增加而线性增加，这样将导致不符合Gustafson
定律的前提条件，而是符合阿姆达尔定律的前提条件。最终得出的加速比将是按照阿姆达尔定律计算出结果。
因此如何消除锁竞争造成的串行化执行就成了程序员需要解决的问题，下面就来先看一下几种不同类型的锁竞争形式对加速比指标的具体影响，在锁竞争的情况中，任务粒度因子和锁粒度因子是影响加速比的重要因素之一，因此需要先看一下任务粒度因子和锁粒度因子的概念。
在一个有锁保护操作的程序中，每个任务中的计算可以分为如下图所示的几部分：
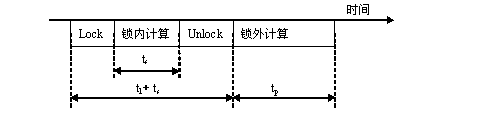
图1
：任务内的计算分类
其中
t
s － 表示锁内计算时间，大小由共享资源的操作时间决定，与共享资源类型有关，并且与程序员的程序设计有关。
t
l － 表示 Lock操作和Unlock操作耗费的时间，如果CPU核的速度固定，那么它为一常量。
t
p － 表示锁外可并行计算部分耗费的时间，大小与具体的应用类型及程序员的分解有关
为了形象地表示出各段计算间的比例关系，引入两个概念：任务粒度因子和锁粒度因子。
1. 任务粒度因子
任务粒度因子主要是用来反映一个任务的计算量大小，由t
l是常量，因此把任务内的有效计算和t
l的比值叫做任务粒度因子，记为：
2. 锁粒度因子
锁粒度因子反映了一个任务内锁操作的粒度关系，用锁内计算和t
l的比值来表示锁粒度因子，记为：
在一个固定式锁竞争情况中，是由若干个同时创建的对等任务竞争同一把锁，在这种固定式竞争环境中，假设每个任务都执行一次锁内操作，锁竞争一定会发生并因锁竞争而导致任务排队串行执行锁操作及锁内计算。固定式锁竞争属于实际情况中的常见现象，比如使用前面提到过的OpenMP来创建任务，如果在任务中使用了锁操作的话，那么它就是一种固定式锁竞争。
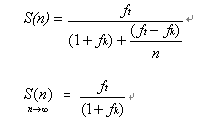
在随机锁竞争中，各个对等任务运行锁计算的时间是随机的。比如在服务器软件中，各个任务创建后，每个任务都在循环地做同样的计算，而各个任务的运行时间受网络客户端的影响，其处理时间不是固定的，而是随机的，这样将导致各个任务在竞争同一把锁时出现随机竞争现象。
随机锁竞争情况下的加速比期望值如下：
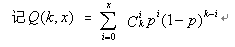
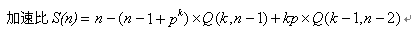
n 随机锁竞争最坏情况下的加速比
上面计算出的加速比是期望值，在最坏情况下，实际上有
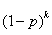的概率所有的任务都处于锁内计算状态，在这种最坏情况下，只有一个任务在运行，因此加速比为1，如果考虑锁计算开销，那么加速比为
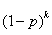的概率所有的任务都处于锁内计算状态，在这种最坏情况下，只有一个任务在运行，因此加速比为1，如果考虑锁计算开销，那么加速比为
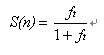
在最坏的情况下，加速比将小于1。
在一个分布式锁竞争环境中，有多个任务竞争多把不同的锁，不妨设有m个任务竞争r把不同的锁。
如果任务数量m足够大的话，那么运行锁外计算的任务数量将会大于CPU核数，导致每个CPU核上都有任务在运行，此时的多CPU效率为
，
，
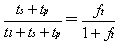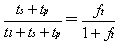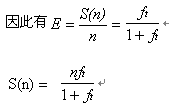
可以看出这种情况下的加速比和CPU核数成正比，并和任务粒度因子有关，任务粒度因子越大，那么加速比也越大。此时加速比和锁粒度没有任何关系。这是分布式锁竞争和普通锁竞争的最大区别。
如果任务数量m不够大，运行锁外计算的任务数量小于CPU核数的话，那么需要计算在有多少个进行锁竞争的任务在运行。
为方便起见 ，令k为运行锁内计算的任务数量，那么这k个任务在竞争r把锁，假设有 1把锁上有任务在竞争，可以求出q的期望值为：
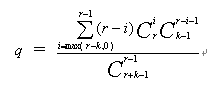
实际上q表示了这些锁竞争的任务中，最多可能有q个任务在运行，最大运行锁内计算的任务数为没有运行锁外计算的CPU核数。
如果q小于n-m+k，那么有m-k个任务在运行锁外计算，有q个任务在运行q把锁上的锁内计算，此时多CPU效率为
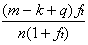，求出加速比的期望值为：
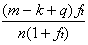，求出加速比的期望值为：
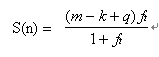
加速比的大小完全取决于q的大小，而q的大小与任务数k和锁的数量r有关，r保持不变情况下，任务数愈大，则q愈大；任务数k保持不变情况下，r愈大则q愈大。
如果q大于等于n-m+k，那么将至少有n个任务在运行，所有的CPU核都处于运行状态，考虑加锁解锁增加的开销后，多CPU效率期望值为
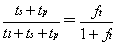，可以求出此时的加速比期望值为：
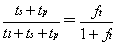，可以求出此时的加速比期望值为：
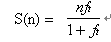
所以在随机分布式锁竞争的情况下，加速比只和四个因素有关，CPU核数、任务粒度因子、任务数量、锁的数量。
只要选取合适的任务数量、锁的数量，那么就可以使加速比和CPU核数成正比关系。
n 分布式锁竞争在最坏情况下的概率计算
分布式锁竞争情况下，考虑一种最坏的情况，所有的任务都在运行锁内计算，此时可以
只要选择合适的任务数m，锁数量r，那么可以将概率P控制在一个比较大的值，这样在最坏情况下也不会出现问题。
以上三种锁竞争形式中，固定式锁竞争所得到的加速比是很糟糕的，和阿姆达尔定律相当，随机式锁竞争所得到的加速比比固定式好了许多，但最坏情况下仍然不容乐观。分布式锁竞争所得到的加速比是最好的，加速比和CPU核数成正比，和Gustafson定律描述的相当。因此在多核系统中使用分布式锁竞争的话，可以取得和单核系统中多任务编程差不多的性能。分布式锁竞争形式将是多核编程的发展方向。
【1】
G.M. Amdahl, Validity of the single-processor approach to achieving large scale computing capabilities. In AFIPS Conference Proceedings vol. 30 (Atlantic City, N.J., Apr. 18-20). AFIPS Press, Reston, Va., 1967, pp. 483-485.
【2】
J.L. Gustafson, , Reevaluating Amdahl's Law, CACM, 31(5), 1988. pp. 532-533.
【3】J. L. Gustafson, G.R. Montry, and R.E. Brenner,
Development of parallel methods for a 1024-processor hypercube. SIAM Journal on Scientific and Statistical Computing vol.9, No.4, July 1988.
【4】
S. Krishnaprasad, Uses and Abuses of Amdahl’s Law
【5】
C. S. Chang and R. Nelson, Bounds on the Speedup and Efficiency of Partial Synchronization in Parallel Processing Systems Journal of the Assocation for Computmg Machinery Vol 42, No 1. January 1995. pp. 204–231
【6】
Julia Lipman and Quentin F. Stout, A Performance Analysis of Local Synchronization
【7】Yuan Shi，
Reevaluating Amdahl's Law and Gustafson's Law. 1996.
扫一扫
645
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
