CF1764D Doremy‘s Pegging Game

题目描述

Doremy has $n+1$ pegs. There are $n$ red pegs arranged as vertices of a regular $n$ -sided polygon, numbered from $1$ to $n$ in anti-clockwise order. There is also a blue peg of slightly smaller diameter in the middle of the polygon. A rubber band is stretched around the red pegs.

Doremy is very bored today and has decided to play a game. Initially, she has an empty array $a$ . While the rubber band does not touch the blue peg, she will:

1. choose $i$ ( $1\le i\le n$ ) such that the red peg $i$ has not been removed;
2. remove the red peg $i$ ;
3. append $i$ to the back of $a$ .

Doremy wonders how many possible different arrays $a$ can be produced by the following process. Since the answer can be big, you are only required to output it modulo $p$ . $p$ is guaranteed to be a prime number.
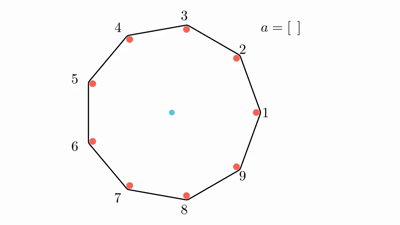game with $n=9$ and $a=[7,5,2,8,3,9,4]$ and another game with $n=8$ and $a=[3,4,7,1,8,5,2]$

题意简述

在墙上有 $n$ 个红色的大钉子，编号为 $1\dots n$。有一根橡皮筋围在钉子上，形成了一个
正 $n$ 边形。在正 $n$ 边形的中心处有一个蓝色的小钉子，蓝色钉子的直径比红色钉子小。现
在你拔掉若干红色钉子，当橡皮筋最终碰到了蓝色钉子，游戏结束。问你有多少种有序的拔
掉红色钉子的方案。答案模一个质数 $p$.

题解

由于蓝色钉子的直径比红色钉子小，所以如果 $n$ 为偶数，红钉子只剩一条直径的两个时，不会碰到蓝钉子。

所以若 $n$ 为偶数，考虑最后剩下一条直径的钉子，其他 $(n-2)$ 个钉子随便拔，最后两个钉子二选一拔，有 $\frac{n}{2}$ 条直径，故方案数为 $n\cdot (n-2)!$。

现在考虑一般情况。设 $t=\lfloor \frac{n}{2}\rfloor$

观察最后结束钉子的位置，发现最少有长度为 $t$ 的区间钉子被拔光，且这样的区间只有一个。

我们枚举被拔掉的区间长度 $i$ 从 $t$ 到 $n-2$ 。
为什么枚举到 $n-2$ 呢？因为区间外的两个钉子不能拔掉，否则长度会增加。
下面放个图方便理解
上图为 $n=9$ 的情况。
如图，黑圈为被拔掉的区间，橙色三角形部分即为可能被拔的钉子的位置。在橙色三角形外的区间内的钉子，容易看到橡皮筋会碰到蓝钉子，是不合法的。

下图为 $n=10$ 的情况
有三个钉子可作为最后一个被拔掉的钉子。

通过上两个图可发现，最后一个被拔掉的钉子的可能位置的数量为 $2t-i$。

接下来枚举区间外的钉子中拔去 $j$ 个钉子，从 $0$ 到 $n-i-2$。区间外两旁的钉子是不能拔的，上面已经说过了。

从可拔的 $(n-i-2)$ 个钉子选 $j$ 个钉子拔，然后区间内 $i$ 个钉子全拔完，区间外要拔 $j$ 个钉子，并且有一个钉子是要最后拔的，由于要考虑顺序，所以方案再乘上 $(i+j-1)!$

这样的长度为 $i$ 的区间有 $n$ 个。

所以对于长度为 $i$ 的区间，方案即为 $n\cdot (2t-1)\sum _{j=0}^{n-i-2}\left(\genfrac{}{}{0ex}{}{n-i-2}{j}\right)\left(j+i-1\right)!$

时间复杂度 $O(n^2)$

代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll mod,f[5001],inv[5001],ans;
int n;
ll ksm(ll a,ll b)
{
    ll ans=1;
    while(b){
        if(b&1) ans=ans*a%mod;
        b>>=1;
        a=a*a%mod;
    }
    return ans;
}
ll c(ll n,ll m)
{
    if(n<m) return 0;
    return f[n]*inv[m]%mod*inv[n-m]%mod;
}
int main()
{
    scanf("%d%lld",&n,&mod);
    f[0]=1;
    for(int i=1;i<=n;i++) f[i]=f[i-1]*i%mod;
    inv[n]=ksm(f[n],mod-2);
    for(int i=n-1;i>=0;i--) inv[i]=inv[i+1]*(i+1)%mod;
    int t=n/2;
    for(int i=t;i<n-1;i++){
        ll sum=0;
        for(int j=0;j<=n-i-2;j++) sum=(sum+c(n-i-2,j)*f[j+i-1])%mod;
        ans=(ans+sum*n%mod*(2*t-i))%mod;
    }
    if(n%2==0) ans=(ans+n*f[n-2])%mod;
    cout<<ans;
}