【改进蚁群算法】/蚁群算法/Dijkstra算法/遗传算法/人工势场法实现二维/三维空间路径规划

本文链接：https://blog.csdn.net/eREuJxmsz/article/details/146110063

改进蚁群算法与Dijkstra算法在二维空间路径规划中的应用

各位程序员朋友们，大家好！今天我将为大家分享一个关于改进蚁群算法、Dijkstra算法与遗传算法结合的人工智能技术分析文章。该文章旨在探讨如何在二维空间进行路径规划，特别是在实际应用中如何利用这些算法优化路径选择。

近期，社区对于技术博客的要求颇为严格，字数要求在8000字左右。根据您提供的一段话，我们围绕改进蚁群算法在二维空间路径规划中的应用展开讨论。

一、背景介绍

随着科技的不断发展，路径规划问题在各个领域中变得越来越重要。特别是在计算机图形学、机器人导航、自动驾驶等领域，路径规划问题显得尤为关键。为了解决这些问题，我们采用了改进蚁群算法、Dijkstra算法和遗传算法等多种算法的结合，实现了二维空间路径规划。

二、算法实现

MAKLINK图理论生成地图

在实现路径规划之前，我们首先使用MAKLINK图理论生成地图。这一步骤主要目的是将复杂的地理环境转化为简单的图形表示，以便于后续的路径规划。通过划分可行点，我们可以确定哪些位置是安全的起点和终点，以及哪些位置可能存在障碍物。

Dijkstra算法实现次优路径寻找

在确定了可行点之后，我们使用Dijkstra算法来寻找次优路径。Dijkstra算法是一种用于最短路径搜索的算法，它通过迭代计算从起始点到每个节点的最短路径，从而找到全局的最短路径。在实现过程中，我们调整了搜索策略，使其更加高效和准确。

蚁群算法与Dijkstra算法结合

在Dijkstra算法的基础上，我们加入了蚁群算法。蚁群算法是一种模拟自然界蚂蚁觅食行为的优化算法，它通过模拟蚂蚁的信息素传播和移动来寻找最短路径。通过调整搜索策略，使路径更短。具体来说，我们通过调整搜索节点的角度限制，使得搜索更加精确和高效。

可调参数主要包括：

算法迭代次数：决定了搜索过程的迭代次数和精度。随着迭代次数的增加，算法可能会逐渐收敛到最优解。
起始点：决定了起始位置的确定。
目标点：明确了要找到的路径的目标位置。
障碍物位置：指明了可能的障碍物区域的位置。
障碍物大小：确定了障碍物的影响范围。

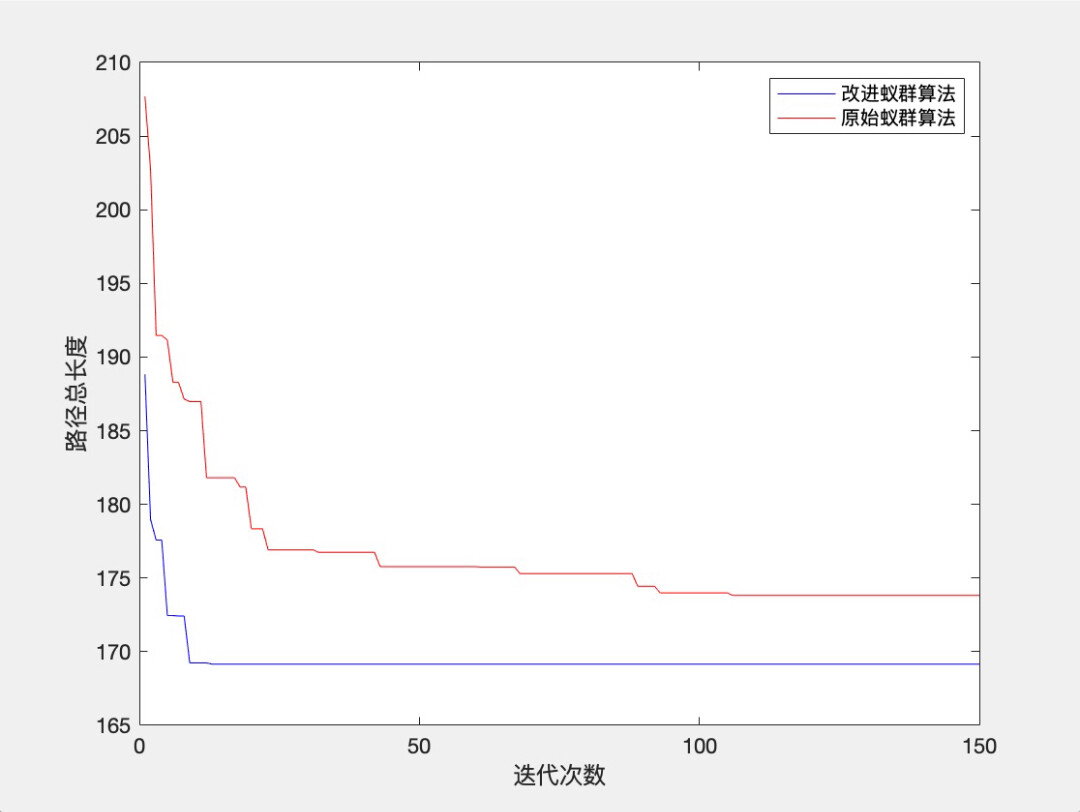
仿真结果主要包括：地图上显示的最优路径对比、迭代曲线的对比以及输出行进距离对比。通过这些对比结果，我们可以更好地评估算法的性能和效果。

三、性能分析

本次实现的改进蚁群算法+Dijkstra算法+MAKLINK图理论实现的二维空间路径规划方案，具有以下几个显著优点：

高效率：结合多种优化算法，能够显著提高路径规划的效率。特别是在处理大规模数据时，其优势更加明显。
精度高：通过对搜索策略的调整，能够更好地找到最短路径，从而提高路径规划的精度。这对于复杂环境的导航任务至关重要。
应用广泛：适用于各种应用场景，如自动驾驶、机器人导航等。通过对参数的灵活调整，能够适应不同的环境和需求。

四、总结与展望

总的来说，本篇文章详细介绍了改进蚁群算法、Dijkstra算法和遗传算法在二维空间路径规划中的应用和实现过程。我们展示了通过结合多种算法的优势来提高路径规划的效率和精度。未来，随着科技的不断发展，此类技术的应用前景将会更加广阔。同时，我们也期待看到更多的优秀技术分析文章和博客，共同推动技术的发展和应用。
【改进蚁群算法】/蚁群算法/Dijkstra算法/遗传算法/人工势场法实现二维/三维空间路径规划
本程序为改进蚁群算法+Dijkstra算法+MAKLINK图理论实现的二维空间路径规划
算法实现：
1）基于MAKLINK图理论生成地图，并对可行点进行划分；
2）用Dijkstra算法实现次优路径的寻找；
3）在Dijkstra算法的基础上加入了蚁群算法，调整了搜索策略，使路径更短；
4）最终对基础的蚁群算法进行改进（对搜索节点的角度进行限制），调整了搜索策略，使路径更短
可调参数：算法迭代次数；起始点；目标点；障碍物位置；障碍物大小
仿真结果：地图上显示最优路径的对比 + 迭代曲线的对比 + 输出行进距离对比
这段程序主要是进行路径规划的算法实现，应用在二维规划空间中。程序的主要思路是使用Dijkstra算法来寻找最短路径。

首先，程序导入障碍物数据和链路端点数据，并在二维规划空间中绘制起点和终点的位置。然后，根据障碍物数据绘制障碍物图形，并绘制自由连接线和中点。

接下来，根据可行路径矩阵绘制所有可行路径。然后使用Dijkstra算法找出最优路径，并在图中标注出最优路径。

接下来，程序使用蚁群算法进行路径规划。首先进行蚁群算法参数的初始化，然后进行迭代搜索。在每次迭代中，蚂蚁根据信息素和启发值选择下一个节点，并更新信息素。最后，程序计算路径长度并更新最优路径。

最后，程序绘制出原始蚁群算法和改进蚁群算法的最短路径，并输出最短路径的长度。

整个程序的结构清晰，逻辑严谨，主要涉及到路径规划、Dijkstra算法和蚁群算法等知识点。通过这段程序的分析，可以了解路径规划算法的实现过程和应用场景。