二叉树的12大问题

转载自：http://blog.csdn.net/randyjiawenjie/article/details/6772145 觉得很好，收藏了

二叉树的常见问题有如下几个，如果解决好了，就跟链表一样轻松：唯一不一样的是，二叉树是非线性结构。常见的问题如下

1. 1.二叉树三种周游（traversal）方式：  
2. 2.怎样从顶部开始逐层打印二叉树结点数据  
3. 3.如何判断一棵二叉树是否是平衡二叉树  
4. 4.设计一个算法，找出二叉树上任意两个节点的最近共同父结点，复杂度如果是O(n2)则不得  
5.   
6. 分。  
7. 5.如何不用递归实现二叉树的前序/后序/中序遍历？  
8. 6.在二叉树中找出和为某一值的所有路径  
9. 7.怎样编写一个程序，把一个有序整数数组放到二叉树中？  
10. 8.判断整数序列是不是二叉搜索树的后序遍历结果  
11. 9.求二叉树的镜像  
12. 10.一棵排序二叉树（即二叉搜索树BST），令 f=(最大值+最小值)/2，设计一个算法，找出距  
13.   
14. 离f值最近、大于f值的结点。复杂度如果是O(n2)则不得分。  
15. 11.把二叉搜索树转变成排序的双向链表  
16. 12.打印二叉树中的所有路径（与题目5很相似）

解决思路：

1.二叉树三种周游（traversal）方式：任何一本数据结构的书都有描述，略过；

2.怎样从顶部开始逐层打印二叉树结点数据？

设置一个队列，然后只要队列不为空，将对首元素的左右孩子加入队列（如果左右孩子不为空），然后将队列的首元素出对即可，如下图所示：

二叉树如下图所示：

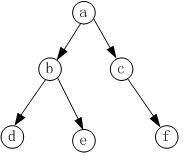
那么，整个过程如下：

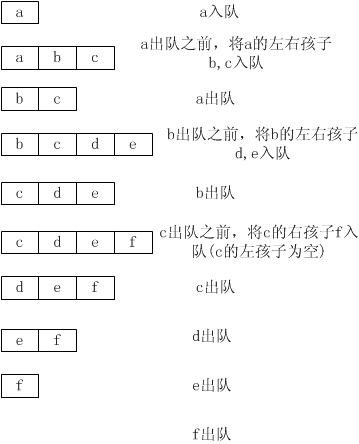
自然，就输出了a,b,c,d,e,f

3.如何判断一个二叉树是否是平衡的？

太简单了，利用递归就可以了：判断根节点的左右子树深度之差是否小于等于1(这里需要用到求深度的方法)，如果是，根节点就是平衡的；然后，在判断根节点的左孩子和右孩子是否是平衡的。如此继续下去，直到遇见叶子节点。一旦不是，立刻返回false;

计一个算法，找出二叉树上任意两个节点的最近共同父结点，复杂度如果是O(n2)则不得分

首先找到这两个点key1和key2，并且记录下找到这两个点的路径Path1和Path2。然后，找到第一个点k满足，key1<k<key2就可以了。

如图：

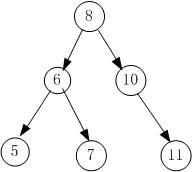
假设key1 = 5，key2 = 7，那么显然，Path1{8,6,5}, Path2{8,6,7}。满足第一个key1<k<key2的k为6。故k = 6。

至于怎么求出Path1和Path2，可以看问题12。

5.如何不用递归实现二叉树的前序/后序/中序遍历？（网易面试就问到了，悲剧了，当时一下子卡住了）

看看书，基本任何一本数据结构的书都有，主要利用栈。

6.在二叉树中找出和为某一值的所有路径？

还是先解决12题目，访问二叉树到叶子节点的任意路径。这个问题解决了，自然求和看是否满足条件就可以了。

7.怎样编写一个程序，把一个有序整数数组放到二叉树中？

递归，还是利用递归：

设有int array[begin,end]，首先将array[(begin + end)/2]加入二叉树，然后递归去做array[begin,(begin + end)/2 - 1]和array[(begin + end)/2 + 1, end]。注意写好函数的形式就可以了。一切都很自然。

8.判断整数序列是不是二叉搜索树的后序遍历结果？

看看吧，后续遍历是这样做的：左右根，所以访问的最有一个节点实际上就是整棵二叉树的根节点root：然后，找到第一个大于该节点值的根节点b，b就是root右子树最左边的节点（大于根节点的最小节点）。那么b前面的就是root的左子树。既然是二叉搜索树的遍历结果，那么在b和root之间的遍历结果，都应该大于b。去拿这个作为判断的条件。

9.求二叉树的镜像？

还是利用递归：只要节点不为空，交换左右子树的指针，然后在分别求左子树的镜像，再求右子树的镜像，直到节点为NULL。

10.一棵排序二叉树（即二叉搜索树BST），令 f=(最大值+最小值)/2，设计一个算法，找出距离f值最近、大于f值的结点。复杂度如果是O(n2)则不得分。

首先，在BST中，最小值就是最左边的节点，最大值就是最右边的节点。
在分别求出min和max后，求出f。然后利用查找，找出一个大于f的节点就可以了。
复杂度为logN。

11.把二叉搜索树转变成排序的双向链表

12..打印二叉树中的所有路径

路径的定义就是从根节点到叶子节点的点的集合。

还是利用递归：用一个list来保存经过的节点，如果已经是叶子节点了，那么打印list的所有内容；如果不是，那么将节点加入list，然后继续递归调用该函数，只不过，入口的参数变成了该节点的左子树和右子树。

程序如下

1. 解答1：自己看书了  
2. 解答2：  
3. //问题2：怎样从顶部开始逐层打印二叉树结点数据  
4. void PrintAtLevel(BiTNode* root){  
5.     vector<BiTNode*> vector;  
6.     vector.push_back(root);  
7.     while(!vector.empty()){  
8.         BiTNode* tmp = vector.front();  
9.         if(tmp->lchild != NULL)  
10.             vector.push_back(tmp->lchild);  
11.         if (tmp->rchild != NULL)  
12.             vector.push_back(tmp->rchild);  
13.         cout << tmp->data << endl;  
14.         vector.pop_back();  
15.     }  
16. }  
17. //问题3：如何判断一棵二叉树是否是平衡二叉树  
18. int isBalencedTree(treeNode* root){  
19.     if (root == NULL)  
20.         return 0;  
21.     int depth1 = getDepth(root->lchild);  
22.     int depth2 = getDepth(root->rchild);  
23.     if (depth1 == depth2 || depth1 == depth2 + 1 || depth1 == depth2 - 1)  
24.         return 1;  
25.     else  
26.         return 0;  
27.     int flag1 = isBalencedTree(root->lchild);  
28.     int flag2 = isBalencedTree(root->rchild);  
29.     if (flag1 && flag2)  
30.         return 1;  
31.     else