解锁动态规划的奥秘：从零到精通的创新思维解析（10）

前言：

        前几天，我写了一篇关于动态规划的文章，今天继续为大家带来一些动态规划相关的习题解析。本次分享的两道题依然围绕“股票”问题展开，不过相比之前的题目，难度有所提升。希望能为大家的学习提供帮助！

1.买卖股票的最佳时机

1.1.题目来源

        本题目来源于力扣，下面小编给出它的链接：121. 买卖股票的最佳时机 - 力扣（LeetCode）

1.2.题目解析

        本题是小编之前讲解的股票问题的升级版。它实际上是一个经典的股票问题，因为在这一版本中，既没有交易手续费，也没有冷却期。问题的状态很直观：分为买入和卖出两种状态。不过，与之前的版本不同的是，本题对交易次数有限制——我们只能进行一次交易。也就是说，我们需要找到最佳的两天进行买入和卖出操作，从而获得最大的利润。

        本题的难点在于如何高效地找到理论上的最大利润。接下来，小编将详细讲解本题的解题思路。

1.3.思路解析

1.状态表示

        对于动态规划类型的题目，我们通常都需要设置好dp表来帮助我们进行状态的分析，本题小编将会使用两个二维的dp表来表示出本题的两个状态，首先这两个状态方程分别表示买入状态和卖出状态，行号代表着第几天，列号代表着第几次；这样我们通过一个二维的数组就可以表示出本题目的状态，其状态的详细表示如下所示。

f[i][j]; //到达第i天的时候，完成了j次交易，进入了买入状态，此时的最大利润。
g[i][j]; //到达第i天的时候，完成了j次交易，进入了卖出状态，此时的最大利润

2.状态转换方程

        此时我们就可以根据状态进行状态方程的书写了，对于买卖股票的题目，小编认为通过书写状态机来表示出状态转换方程是比较不错的方法，状态机的介绍我在之前的文章写过，想要了解的读者可以直接跳到那篇文章：解锁动态规划的奥秘：从零到精通的创新思维解析（9）-CSDN博客，下面我就带领各位一步一步的书写状态机。

首先我们先表示出两种状态：

之后我们知道前一天是买入状态的话，第二天可以仍然手里攥着股票，或者是把股票卖出去（此时就是代表着交易的次数-1）：

如果前一天是卖出状态的话，那么第二天仍然可以不买股票，或者是选择买入股票：

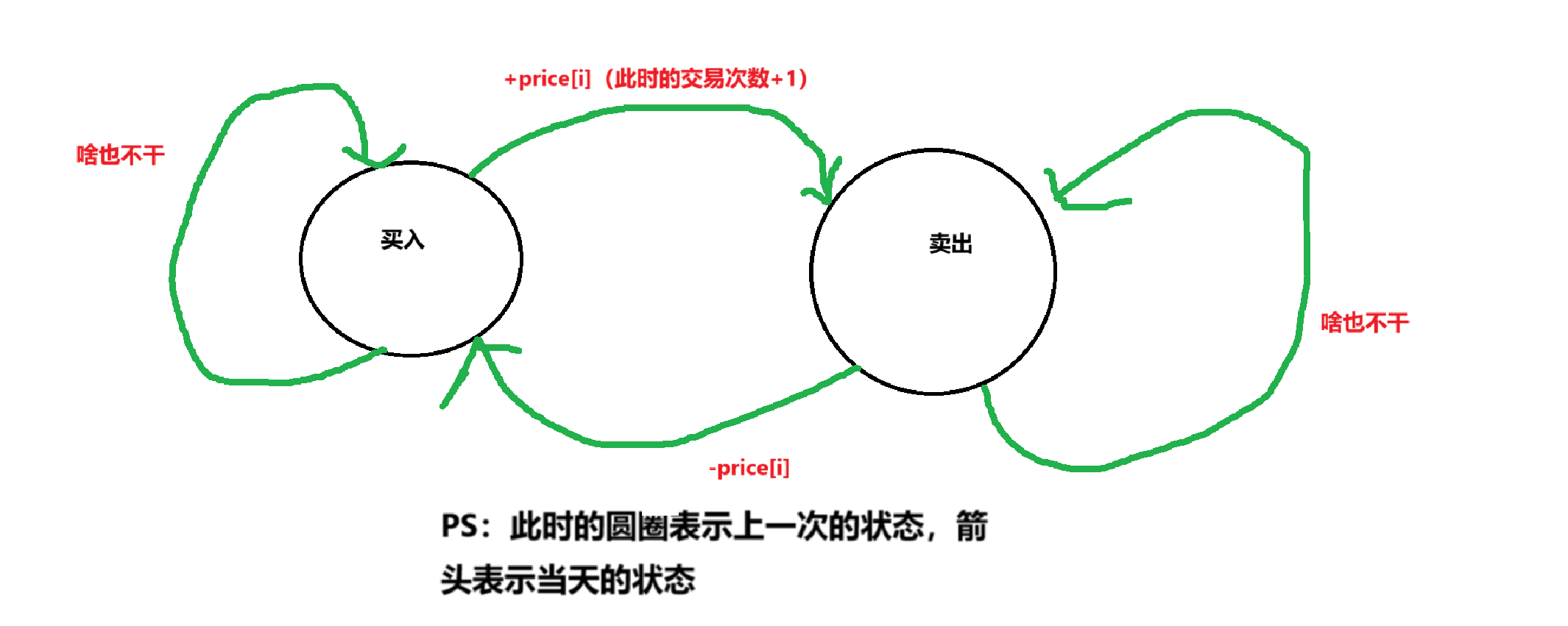
        以上就是状态机的表示方法，可能很多读者朋友会奇怪，为什么我会选择在卖出的时候才让交易次数+1，因为我的理解是：一次完整的交易应当是包含买入和卖出，仅仅有其中一个是不够的，可以选择在买入的时候就让交易次数的+1，也可以和我一样，在卖出的时候选择让交易次数+1，这个全凭个人的喜好。通过上面的状态机，我们完全可以写出状态转换方程，此时需要借助最大值函数：

f[i][j] = max(f[i-1][j],g[i-1][j]-price[i]);
g[i][j] = max(g[i-1][j],f[i-1][j-1] + price[i]);  //这个写法其实有错误，具体的可以看下面的代码部分，埋下一个小小的伏笔

3.初始化

        对于第一行的数据，我们需要进行一次初始化（这里我就不使用虚拟节点了），对于f [0] [0]，肯定是-price[0]，因为第一天是买入状态的话，只能买当天的股票；g[0] [0]只有可能是0,；而f[0] [1]和g[0] [1]，为了不让他影响结果，统一让它为-0x3f3f3f3f（比最小值大一点，如果用最小值的话过不了），具体如下所示：

f[0][0] = -price[0];
g[0][0] = 0;
f[0][1] = g[0][1] = -0x3f3f3f3f;

4.填表顺序

        肯定还是从左到右，从上到下【这里很好判断，如果需要有用到之前的数据，那就是从左到右/从上到下，如果用到之后的数据，那自然就是反着来了】。

5.返回值

        返回g[n - 1] [j]中的最大项（n表示一共有多少天），这里肯定有读者朋友问了，那么我的f去哪了？这里只要各位捋清楚一件事：这股票是你攥在手上利润大，还是在最佳时机卖掉利润大？

1.4.代码书写

        此时，我们需要先把状态转换方程设置好（两个表），并且根据我上面所说进行初始化操作：

int n = prices.size();  //一共多少天
vector<vector<int>> f(n,vector<int>(2));//买入状态
vector<vector<int>> g(n,vector<int>(2));//卖出状态
f[0][0] = -prices[0],f[0][1] = g[0][1] = -0x3f3f3f3f;

        之后，我们就要进入状态转换方程的书写了，这里我要收回一个伏笔，上面我在状态转换方程的时候曾经说过，g表的书写是错误的，这是因为这里牵扯到了j，因为当j等于0的时候（就比如g[1] [0]），如果此时要卖出股票了，但是此时根据状态方程，我们就要取到g[0] [-1]，这个就是经典的错误，标准的零分，此时我们就需要处理这种情况，废话不多说，我的解决方案是：我们每次填g表的时候，先让其为之前是啥也不干的状态，此时判断g-1是否大于等于0，如果符合这个情况，我们在和买入状态进行最大值的取舍，具体写法如下所示：

for(int i = 1 ; i < n ; i++)
{
    for(int j = 0 ; j < 2 ; j++)
    {
        f[i][j] = max(f[i - 1][j],g[i - 1][j] - prices[i]);
        g[i][j] = g[i - 1][j];
        if(j - 1 >= 0 ) g[i][j] = max(g[i][j],f[i - 1][j - 1] + prices[i]);
    }
}

        这里我不得不感慨一下，算法题真的是坑多，一不小心就会掉入一个坑里，有时候掉到坑里可能我们都不自知，所以这就告诫我们，做任何的习题，我们都要细心细心再细心！

        之后我们直接通过循环（此题不需要）找到最大值即可：

return max(g[n - 1][0],g[n - 1][1]);

1.5.总代码展示

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        vector<vector<int>> f(n,vector<int>(2));//买入状态
        vector<vector<int>> g(n,vector<int>(2));//卖出状态
        f[0][0] = -prices[0],f[0][1] = g[0][1] = -0x3f3f3f3f;
        for(int i = 1 ; i < n ; i++)
        {
            for(int j = 0 ; j < 2 ; j++)
            {
                f[i][j] = max(f[i - 1][j],g[i - 1][j] - prices[i]);
                g[i][j] = g[i - 1][j];
                if(j - 1 >= 0 ) g[i][j] = max(g[i][j],f[i - 1][j - 1] + prices[i]);
            }
        }
        return max(g[n - 1][0],g[n - 1][1]);
    }
};

2.买卖股票的最佳时机III

2.1.题目来源

        老规矩，我先把题目的链接发一下：123. 买卖股票的最佳时机 III - 力扣（LeetCode）

        本题其实和上题比较类似，但还是有一些区别的，就比如上面的这个题目，告诉我们最多可以完成两笔交易，而第一个题目我们仅仅就可以完成一次交易，所以其实仔细一看这俩题目简直就是同根生（这里我继续留下一个伏笔，下个题目就会揭晓为什么他俩这么像~）。

2.3.思路解析

1.状态表示

        和上个题一样，这个题目我们也是需要用到两个表来进行状态表示，分别表示“买入”状态和“卖出”状态。同样的，它们也均是一个二维数组，行号代表着第几天；列号代表着完成了几次交易，合起来就是：在第i天完成了j次交易后的最大利润。

f[i][j]; //到达第i天的时候，完成了j次交易，进入了买入状态，此时的最大利润。
g[i][j]; //到达第i天的时候，完成了j次交易，进入了卖出状态，此时的最大利润

2.状态转换方程

        对于求解状态转换方程，对于买卖股票的问题，我推荐还是使用状态机来完成方程的构建，对于什么是状态机，在我之前的博客亦有记载：解锁动态规划的奥秘：从零到精通的创新思维解析（9）-CSDN博客，感兴趣的读者可以点击来看一下，里面描述的还是比较详细的，下面废话不多说，开始进入状态机的书写。

首先我们先表示出两种状态：

之后我们知道前一天是买入状态的话，第二天可以仍然手里攥着股票，或者是把股票卖出去（此时就是代表着交易的次数-1）：

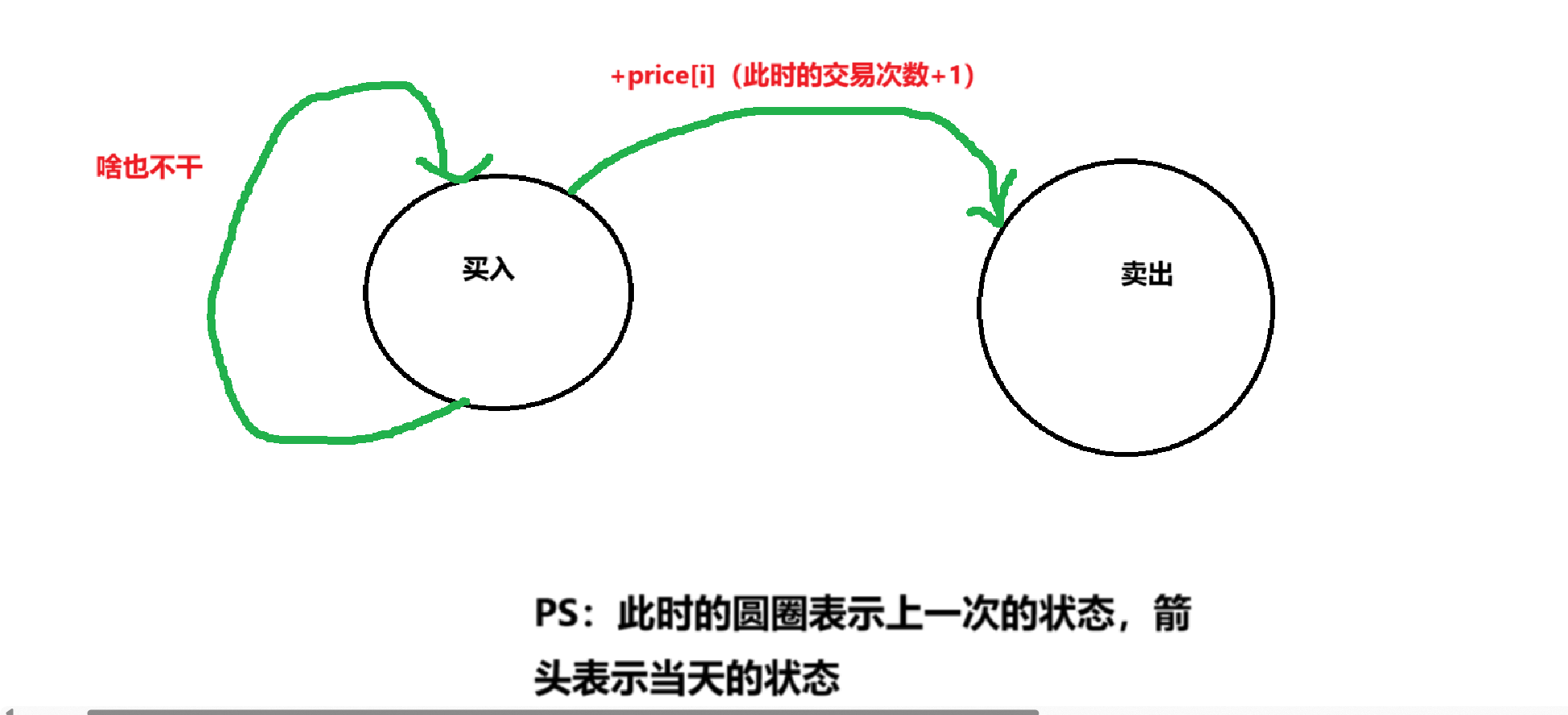
如果前一天是卖出状态的话，那么第二天仍然可以不买股票，或者是选择买入股票：

        可能很多完整读完了本篇文章的读者会很奇怪：主包主包，上面的状态机不是在第一个题目就写了吗？这里我统一回复下，是这样滴，因为考虑到可能有的朋友点开我的文章是为了本题目，本来我想偷懒简写的，想了想，不如把相同的直接复制，这样直接节省了时间。方便了读者，也方便了小编（绝对不是因为懒[○･｀Д´･ ○]）

        表示完状态机以后，我们就可以进行状态转换方程的书写了：可以直接根据上面的图片直接进行方程的填入，我相信聪明的你会直接写出来滴：

f[i][j] = max(f[i-1][j],g[i-1][j]-price[i]);
g[i][j] = max(g[i-1][j],f[i-1][j-1] + price[i]);  //这个写法其实有错误，具体的可以看下面的代码部分，埋下一个小小的伏笔

3.初始化

        对于本题的初始化其实还是比较容易的，不过此时我们需要借助循环的知识，因为按照之前的买卖股票题，我们仅需填充f[0] [0]以及g[0] [0]即可，本题不太一样，此时我们需要把当我们处于第一天（对应着的是数组的0下表位置），此时我们肯定是不需要进行多次交易的，所以此时我们需要把j为1,2的位置填充上一个比较小的数，这里为了不会在运行的时候实例出错，我的建议就是使用：-0x3f3f3f3f来进行初始化即可。

4.填表顺序

        肯定还是从左到右，从上到下【这里很好判断，如果需要有用到之前的数据，那就是从左到右/从上到下，如果用到之后的数据，那自然就是反着来了】。

5.返回值

        返回g[n - 1] [j]中的最大项（n表示一共有多少天），这里肯定有读者朋友问了，那么我的f去哪了？这里只要各位捋清楚一件事：这股票是你攥在手上利润大，还是在最佳时机卖掉利润大？

2.4.代码书写

        此时我们需要创建好两个表，并且根据我给定的初始化条件，对这两个表进行初始化处理。

int n = prices.size();
vector<vector<int>> f(n,vector<int>(3)); //表示的是买入状态第二个表示此时的次数
vector<vector<int>> g(n,vector<int>(3)); //表示的是卖出状态第二个表示此时的次数
f[0][0] = -prices[0],g[0][0] = 0;

        之后我们就要循环进行往表里填充数据了，不过此时填表的时候，可能会出现一个大坑：当我们处于“卖出”状态的第一天的时候，我们需要选取当前的利润的最大值，此时当我们假设前一天为买入状态的时候，此时我们的j为-1，这样的话就会出现经典的错误，标准的零分，此时我们仅需做一个判断就可以解决这个问题了：此时我们在卖出的状态的时候，假设前一天依旧为卖出状态，我们判断j是否大于0，如果大于0的话，那么就和前一天的买入状态进行比较最大值，这样的话我们就把这个坑解决了。之后我们通过两次循环即可。

for(int j = 1 ; j < 3 ; j++)
{
    f[0][j] = -0x3f3f3f3f;
    g[0][j] = -0x3f3f3f3f;  //减少数太小导致负极必反的情况
}
for(int i = 1 ; i  < n ; i++)
{
    for(int j = 0 ;  j < 3 ; j++)
    {
        f[i][j] = max(f[i-1][j],g[i-1][j] - prices[i]);
        g[i][j] = g[i-1][j];
        if(j - 1 >= 0) g[i][j] = max(g[i-1][j],f[i-1][j-1] + prices[i]);
    }
}

        之后直接返回最终的最大值即可。

return max(g[n-1][0],max(g[n-1][1],g[n-1][2]));

2.5.总代码展示

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int n = prices.size();
        vector<vector<int>> f(n,vector<int>(3)); //表示的是买入状态第二个表示此时的次数
        vector<vector<int>> g(n,vector<int>(3)); //表示的是卖出状态第二个表示此时的次数
        f[0][0] = -prices[0],g[0][0] = 0;
        for(int j = 1 ; j < 3 ; j++)
        {
            f[0][j] = -0x3f3f3f3f;
            g[0][j] = -0x3f3f3f3f;  //减少数太小导致负极必反的情况
        }
        for(int i = 1 ; i  < n ; i++)
        {
            for(int j = 0 ;  j < 3 ; j++)
            {
                f[i][j] = max(f[i-1][j],g[i-1][j] - prices[i]);
                g[i][j] = g[i-1][j];
                if(j - 1 >= 0) g[i][j] = max(g[i-1][j],f[i-1][j-1] + prices[i]);
            }
        }
        return max(g[n-1][0],max(g[n-1][1],g[n-1][2]));
    }
};

3.总结

        在股市的江湖里，如何用两次交易抓住财富密码？这篇动态规划攻略堪称《韭菜的自我修养》plus pro max版！我们用f数组表示"此刻必须装深沉"的持股市态，用g数组演绎"落袋为安后假装淡定"的卖出入圣。状态转移就像在贪婪与恐惧之间反复横跳，交易次数限制仿佛在说："年轻人，耗子尾汁"。

        最后在三种交易次数的结局中选最大收益时，像极了成年人表示："我全都要！"。从此炒股代码写得比大妈广场舞还丝滑，收益算得比算命先生还精准。各位代码修仙的大佬们，我们下期在算法的世界里继续御剑飞行，保不准哪天就能用动态规划算出桃花运呢！（手动狗头）。

        五一劳动节到啦，祝各位代码打工人键盘敲出火花，摸鱼摸出境界，搬砖搬成架构师！愿你们的程序无bug，需求不改稿，调休不调休都开心（反正AI不过节，但人类得快乐啊）～ 咱们下篇文章继续用算法征服世界，毕竟——劳动（coding）最光荣！（狗头保命撤退）