AVL的c++详解——删除

前面介绍了平衡二叉树的插入操作：平衡二叉树的插入，这里来介绍平衡二叉树的删除，平衡二叉树是一棵带有平衡条件的二叉查找树，其删除操作是在二叉查找树的基础上添加平衡调整算法。

二叉查找树的删除操作参见博文：二叉查找树的删除（第七点）

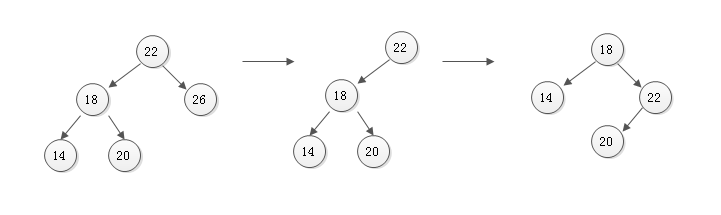
先看一下示意图（）

[cpp]  view plain  copy

 print ?

1. /*二叉查找树的性质让我们可以很方便的查找最小最大键值*/  
2. /*查找最小键值节点：直接递归遍历左子树叶子节点*/  
3. AvlNode* AvlTree::findMin(AvlNode *node)  
4. {  
5.     if (NULL == node)  
6.         return NULL;  
7.   
8.     else if (NULL == node->leftchild)  
9.         return node;  
10.   
11.     else  
12.         return findMin(node->leftchild);  
13. }  
14.   
15. /*非递归实现查找最大键值节点*/  
16. AvlNode* AvlTree::findMax(AvlNode *node)  
17. {  
18.     if (node != NULL)  
19.     {  
20.         while (node->rightchild)  
21.             node = node->rightchild;  
22.     }  
23.   
24.     return node;  
25. }  
26.   
27. void AvlTree::Delete(int val)  
28. {  
29.     if(NULL == Root)  
30.         return;  
31.     else  
32.         Delete(Root, val);  
33. }  
34.   
35. //节点的删除就是不断的交换数据，更改删除节点，最后定位到叶子节点  
36. //  
37. void AvlTree::Delete(AvlNode *&node, int val)  
38. {  
39.     AvlNode *tempnode = NULL;  
40.     if(NULL == node)  
41.         return;  
42.   
43.     else if(val < node->data)  
44.         Delete(node->leftchild, val);  
45.     else if(val > node->data)  
46.         Delete(node->rightchild, val);  
47.   
48.     //find the val  
49.     else if(node->leftchild && node->rightchild)  
50.     {  
51.         tempnode = findMin(node->rightchild);  
52.         node->data = tempnode->data;  
53.         Delete(node->rightchild, node->data);   //理解！待删除节点键值变换  
54.     }                                           //此后要删除的键值节点不是val  
55.     else  
56.     {  
57.         if(node->leftchild && (NULL == node->rightchild))  
58.         {  
59.             tempnode = findMax(node->leftchild);  
60.             node->data = tempnode->data;  
61.             Delete(node->leftchild, node->data);  
62.         }  
63.         else if (node->rightchild && (NULL == node->leftchild))  
64.         {  
65.             tempnode = findMin(node->rightchild);  
66.             node->data = tempnode->data;  
67.             Delete(node->rightchild, node->data);  
68.         }  
69.         else  
70.         {  
71.             delete(node);  
72.             node = NULL;  
73.         }  
74.     }  
75.   
76.     if (node)   //必须添加这个条件，利用递归的力量，调整平衡  
77.     {    
78.         //平衡判断  
79.         if (2 == Height(node->leftchild) - Height(node->rightchild))  
80.         {  
81.             //情况判断  
82.             if (Height(node->leftchild->leftchild) >= Height(node->leftchild->rightchild))  
83.                 RotationLeftOnce(node);  
84.             else  
85.             {  
86.                 RotationRightOnce(node->leftchild);  
87.                 RotationLeftOnce(node);  
88.             }  
89.         }  
90.   
91.         if (2 == Height(node->rightchild) - Height(node->leftchild))  
92.         {  
93.             if (Height(node->rightchild->rightchild) >= Height(node->rightchild->leftchild))  
94.                 RotationRightOnce(node);  
95.             else  
96.             {  
97.                 RotationLeftOnce(node->rightchild);  
98.                 RotationRightOnce(node);  
99.             }  
100.         }  
101.     }  
102. }  

上面的删除操作具体参见：二叉查找树的删除，另外平衡二叉树的查找，遍历与二叉查找树一样。

二、清空二叉树（析构函数）

[cpp]  view plain  copy

 print ?

1. void AvlTree::MakeEmpty(AvlNode *&node)  
2. {  
3.     if (node)  
4.     {  
5.         MakeEmpty(node->leftchild);  
6.         MakeEmpty(node->rightchild);  
7.         delete node;  
8.     }  
9.     node = NULL;  
10. }  

三、平衡二叉树时间复杂度分析

平衡二叉树在二叉查找树的基础上添加了旋转算法，但是旋转操作仅仅改变少数指针的指向，耗费常数时间，平衡二叉树加入了平衡机制，所以其深度为logN，查找、插入和删除在平均和最坏情况下都是O(logN)。对比二叉查找树，时间上稳定了很多