推荐系统是目前非常受欢迎的一个机器学习应用。下面将以电影推荐为例子简单介绍实现推荐系统的方法。
前提
假设我们运营一个电影网站,每个用户可以对电影评分:0-5分。
n(u) 代表用户数量
n(m) 代表电影数量
r(i,j) 代表用户j是否对电影i进行评分。1 已评。0 未评
y(i,j) 代表用户j对电影i的评分。
目的
推荐系统的目的是运行算法,预测用户对他们没打过分的电影的分数,然后进行推荐。
步骤
假设,如下图:
1.我们已经提取出了每个电影的两个特征:属于爱情电影、动作电影的程度。即为X向量。n=2。
2.我们已经收集了部分用户对电影的评分。
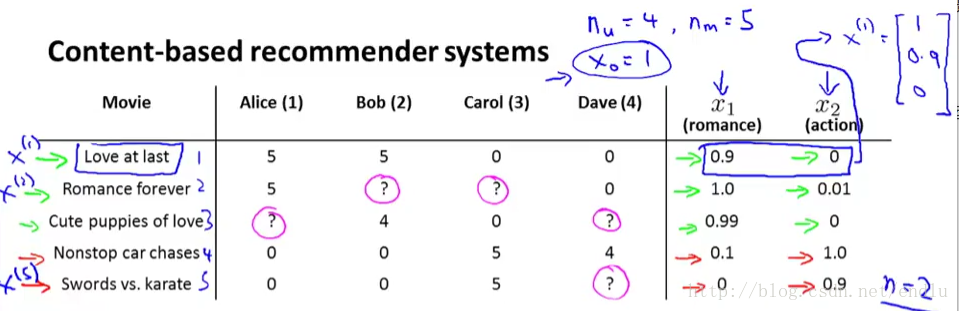
我们的目的就是训练θ参数,得到预测模型y=θ’X,可以对某用户对应电影的评分进行预测。
损失函数、梯度下降,如下:

损失函数:对所有用户已经评分过的电影,均方误差,加上正则项。(这里前后两项消除了分母常数m,对结果θ没有影响)。
梯度下降:括号内部分是损失函数对θ(j)的偏微分。
与线性回归的区别就是约掉了分母常数m。
当然,我们也可以使用更高级的优化算法。
协同过滤
上面我们假设已经提取了电影的特征,但实际情况中,我们可能并不能、或者很难得到这些特征。协同过滤算法能自行的学习索要使用的特征。
首先,假设我们得到部分用于对电影的评分,和用户对不同类型电影的喜好程度,如图:
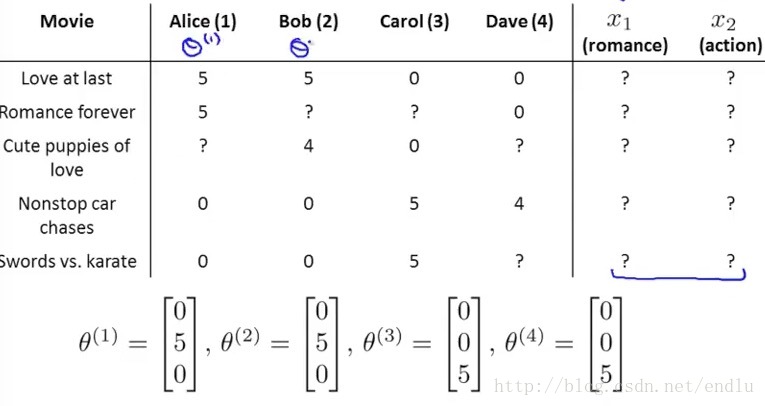
θ为用户对不同电影类型的喜好程度。如上面的问题相反,每个电影属于各类型的程度是未知的。那么通过θ和用户的评分可以学习出电影属于各类型的程度X:
那么,X和θ就变成了鸡生蛋蛋生鸡的问题。
协同过滤的做法是,先随机θ,利用θ学习出X,再利用X学习θ,如此反复,最终收敛到一个较好的结果。
又有优化的公式:
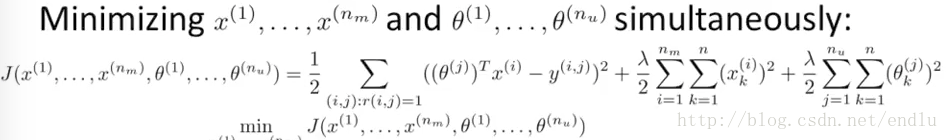
该公式将两个代价函数合并为一个,前半部分与两个代价函数的前半部分是相同的,再加上x和θ的正则化项。该公式的好处是不需要再利用θ学习出X,再利用X学习θ。而是直接计算出结果。























 1051
1051

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








