Scala偏函数、异常、Lazy值编码之编程进阶（5）

本篇文章主要讲述Scala函数式编程之偏函数，异常，及Lazy。

一：偏函数（Partial）定义

  偏函数：当函数有多个参数，而在使用该函数时不想提供所有参数（比如函数有3个参数），只提供0~2个参数，此时得到的函数便是偏函数。

object HelloPartialFunction {
  def main(args: Array[String]): Unit = {
    val sample = 1 to 10
   /* val isEven: PartialFunction[Integer, Unit] ={
      case x if x % 2 ==0 => println(x+ " is even")
      case _ => println("other")
    }*/
     val isEven: PartialFunction[Int, String] ={
      case x if x % 2 ==0 => x+ " is even"

    }
    isEven(4)
    val enevNumbers = sample.collect(isEven)
//    enevNumbers.foreach (println)

    val isOdd: PartialFunction[Int,String]={
      case x if x % 2 == 1 => x + "is odd"
    }
    val numbers = sample.map (isEven orElse isOdd)
    numbers.foreach{println}
  }
}

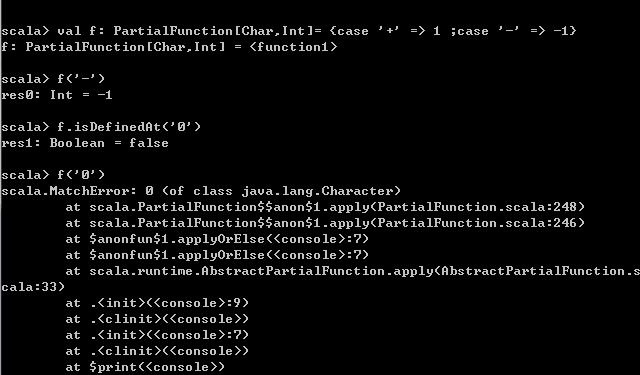
被包在花括号的一组case语句是一个偏函数_一个并非对所有输入值都有定义的函数。他是PartialFunction[A,B]类的一个实例。（A是参数类型，B是返回类型）该类有两个方法：apply方法从匹配到模式计算函数值，而isDefinedAt方法在输入至少匹配其中一个模式时返回true。

说明：偏函数表达式必须位于编译器可以推断出返回类型的上下文中，当你把它赋值给一个带有类型声明的变量，或者将它作为参数传递时，都符合这个要求。

二：异常、Lazy值编码：

object HelloExceptionAndLazyValue {
  def main(args: Array[String]): Unit = {
    try{
        1/0
    }catch {
      case ioException:IOException => println("IOException:" + ioException.toString())
      case illegalArgs:IllegalArgumentException => println("IllegalArgumentException:" + illegalArgs.toString())
      case arithmeticInstruction:ArithmeticInstruction =>("ArithmeticException"+arithmeticInstruction.toString())
    }  finally{

    }
//    val score = 100
    lazy val score = 100
    println("......"+score)
    println("......")
  }
}

被lazy修饰的只有在被调用的时候才会实例化