引导滤波Guided Filter

概念

一句话概括：通过对引导图像对线变换，结合局部线性模型，对原始图像进行滤波处理的算法。

局部线性模型

该模型认为，某函数上一点与其邻近部分的点成线性关系，一个复杂的函数就可以用很多局部的线性函数来表示，当需要求该函数上某一点的值时，只需计算该点线性函数的值并做平均即可。

应用于图像

假设在一个局部窗口内，满足一个线性关系
I 引导图像
q 滤波后的图像
p 原始图像
引导图像做线性变换之后，要与原始图像尽量接近，且模型尽量简单。
1. 假设图像是一个二维函数，且输入输出在一个二维窗口内满足线性关系：

$$q_i=a_kI_i+b_k,\forall i \in {\omega _k}$$
其中q是输出像素的值，I是输入图像的值，i和k是像素索引，a和b是当窗口中心位于k时该线性函数的系数。输入图像不一定是待滤波图像，也可是是其他图像即引导图像，这也是称为引导滤波的原因。对上式两边取梯度，得：
$$\nabla q = a\nabla I$$
即当输入图像I有==梯度==时，输出q也有类似的梯度，因此引导滤波有==边缘保持特性==。
2. 求线性函数的系统，即线性回归。目标函数让拟合函数的输出值和真实值p之前差距最小，即\
// 建立模型的一般套路：==min（经验风险+正则项）==
$$E({a_k},{b_k})=\sum\limits_{i \in {\omega _k}} {({{({a_k}{I_i} + {b_k} - {p_i})}^2} + \varepsilon a_k^2)}$$
其中p待滤波的图像， $\varepsilon$防止系数a过大。
最小二乘(平方)法求解：

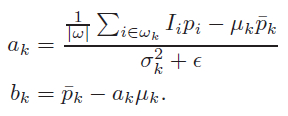
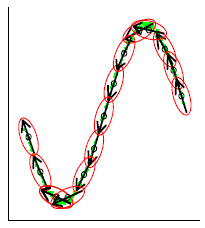
一个像素会被多个窗口包含，即==每个像素由多个线性函数描述==。因此，某一点的输出值时，主需要将所有包含该点的线性函数平均即可，如下：

$${q_i} = \frac{1}{{\left| \omega \right|}}\sum\limits_{k:i \in {\omega _k}} {({a_k}{I_i} + {b_k})} = {{\bar a}_i}{I_i} + {{\bar b}_i}$$
其中w_k是所有包含像素i的窗口，k是这些窗口的中心位置。

功能

• 平滑
• 去噪
• 图像去霾
• 图像增强

参考论文：Guided Image Filtering
拓展阅读：最小二乘法