并查集学习笔记

        本篇是笔者《C++算法学习笔记》专栏的第一篇进阶数据结构——并查集的学习笔记，由于数据结构的特殊性，本篇不再以某道具体的题目详细展开，而是并举多个并查集的使用场景和方法，从而整理这种数据结构的特色与核心思想。

并查集

最基础结构-单链表

        最基础的并查集结构单位是p[x] = y，其中x是当前节点的序号，y是x的父节点的序号。当y=x时，表明当前结点的父节点是自身，或者说没有父节点，这样的节点是根结点。最简单的并查集结构应用便类似一个单链表。与传统的单链表最大区别在于：并查集的实现依靠数组，以此可以实现对单独结点p[x]的直接操作。也正是如此，并查集的“链式结构”并不是并查集的全部，并查集更像是一个优化了节点联系的集合，因此它是并查集，而不是并查链表。

        下图这个并查集是最基础却也是最基本的并查集结构，是所有并查集结构的核心所在，后面的所有进阶拓展都建立在此基础之上。

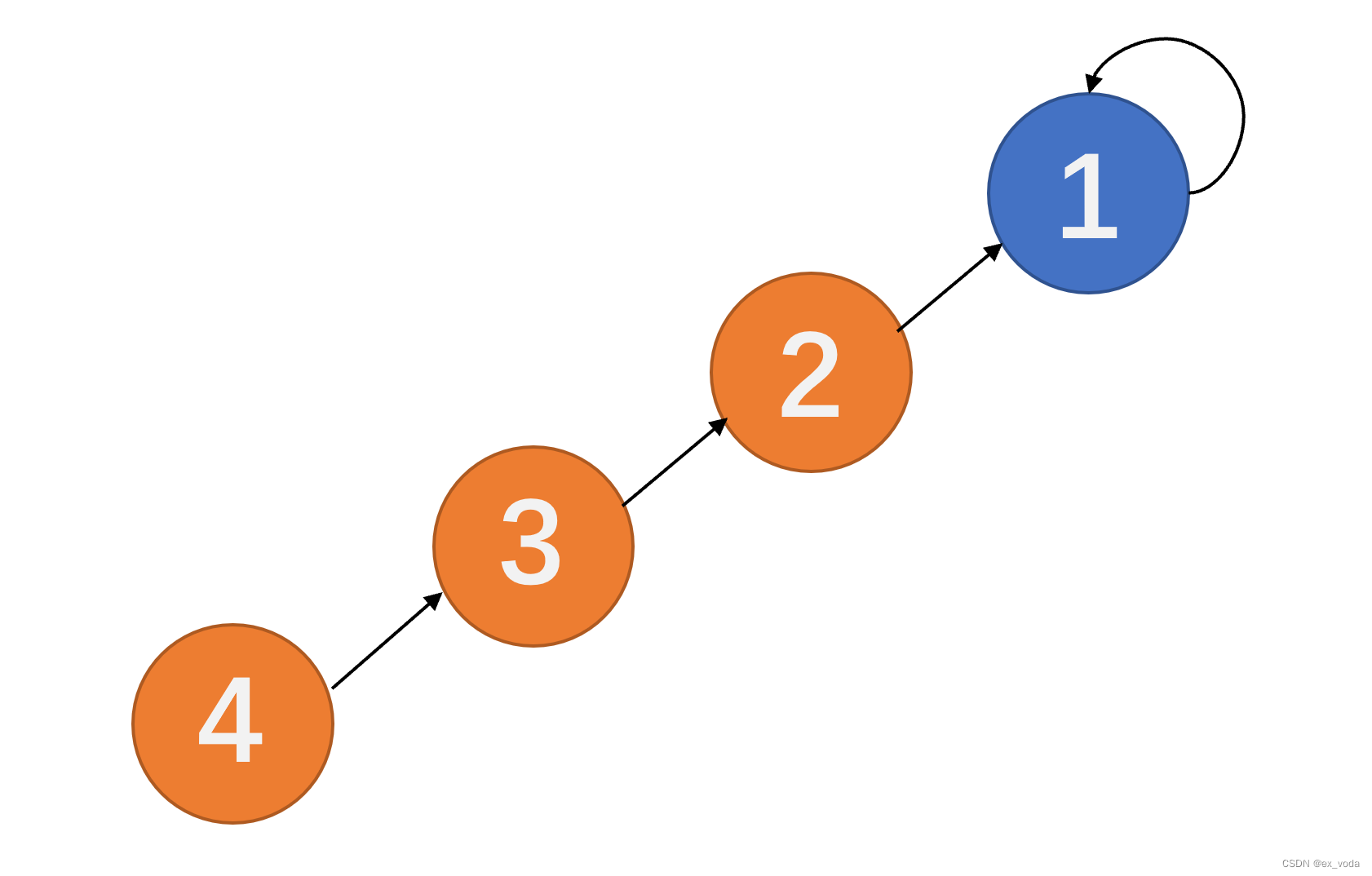
基础操作-初始化函数Init

        并查集的初始化是将每个节点的父节点赋值为其自身，保证在一切开始之前，它们之间没有任何关系。

void Init(int n){
    for(int i=1;i<=n;i++)
        p[i] = i;
}

 基础操作-查询根节点函数Find

        并查集的“查”，表示并查集的最重要操作——查询，并查集的根节点p[x]=x往往具有特殊意义，Find函数能够帮助我们根据任意节点x找到它的根节点的具体标号，有三种写法：

（1）循环型

int Find(int x){
    while(p[x]!=x){
        x = p[x];
    }
    return x;
}

（2）递归型

int Find(int x){
    if(p[x] == x)    return x;
    else    return Find(p[x]);
}

 (3)耍帅型

int Find(int x){
    return x == p[x] ? x : Find(p[x]);
}

基础操作-合并函数Merge

        并查集的“并”，表示并查集另一个最重要的操作——合并，我们希望能过把两个并查集合并为一个，或者把某个游离的节点接到某个并查集上去，无论如何，Merge函数允许我们这么做。

void Merge(int x, int y)
{
    p[Find(y)] = Find(x);
}

进阶操作-边查找边合并函数（路径压缩）MergeFind

        很多时候，我们不希望整个并查集像链一样冗长，这不利于查找和修改的进行，最好整个并查集的高度是很低的，所有的节点的父节点都指向唯一的根节点。

         MergeFind函数帮助我们做出这种优化，其也有三种写法：

（1）循环型

int MergeFind(int x){
    int t=x;
    while(p[t]!=t) t=p[t];
    while(x!=t)
    {
        int temp=p[x];
        p[x]=t;
        x=temp;
    }
    return t;
}

（2）递归型

int MergeFind(int x){
    if(p != p[x])    p[x] = MergeFind(p[x]);
    return p[x];
}

（3）耍帅型

int MergeFind(int x)
{
    return x == p[x] ? x : (p[x] = MergeFind(p[x]));
}

进阶操作-按秩合并

        在进入这个模块之前，我们先需要了解什么是秩，事实上可以把它称为树的高度。额外地记录秩的差异会帮助我们避免并查集在合并的时候往更复杂的方向（秩更高的方向）发展。比如在下图中，右边的树的高度更小，整体复杂性就更低一些。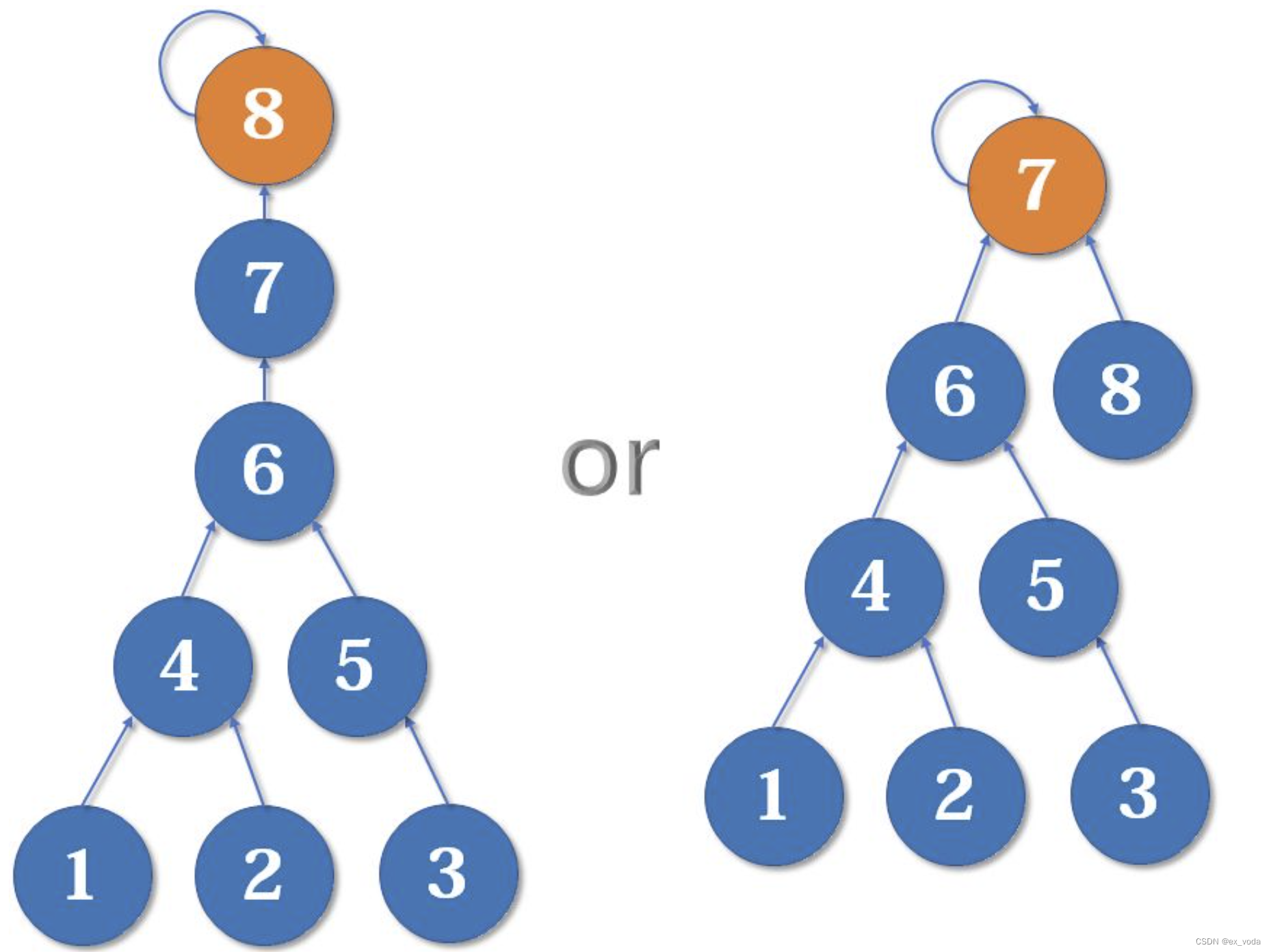

        为了实现这一目的，往往用一个额外的rank[]数组来储存每一个节点的秩，当然，你也可以把它们和节点本身融合成一个结构体节点，不过这部分的内容会在后序介绍，在这里，我们先使用rank[]。

        采用了秩的思想后，我们需要在初始化的同时将秩的信息也初始化，RankInit函数。

void RankInit(int n){
    for (int i = 1; i <= n; i++){
        p[i] = i;
        rank[i] = 1;
    }
}

        查询函数的没有变化的，因为我们只是想找到根节点的位置，与秩无关，它仍是Find。

        需要注意的是，在考虑了秩的时候，请时刻记得关注它的变化：当你为某一个节点赋予父节点的时候，它本身以及它后面的每一个子节点的秩都会一起变化，这不再像普通并查集的合并那么简单，只需要考虑节点的赋值就行，我们不得不需要一个完整的函数RankMerge来处理这种合并操作，最后给出RankMerge函数的实现，它能够更具两棵树的秩的大小选择合并的方向。

void RankMerge(int x, int y)
{
    int x_i = Find(x), y_i = Find(y);    //先找到两个根节点
    if (rank[x_i] <= rank[y_i])
        p[x_i] = y_i;
    else
        p[y_i] = x_i;
    if (rank[x_i] == rank[y_i] && x_i != y_i){
        p[y_i] = x_i;
        rank[x_i]++;                   //如果深度相同且根节点不同，则新的根节点的深度+1
    }
}

---

         到此为止，你已经知晓了所有针对并查集这种数据结构本身的一些操作和优化，但这些始终只停留在理论或者说工具层面，在实际问题中，并查集往往会结合其他数据结构或是一些算法一起使用，接下来笔者会整理一些常见的实际应用模式以供参考，每个应用都会有一道算法题目作为例子，如果可能的话，它会在遇到新用法后被更新。

        注：后面部分所有出现的代码均为伪代码，只是展示程序思路，并不包括完整的功能实现或是题解，所有不包含实现的函数都已在前文给出。

        同时你会注意到后文是按难度排序的，当你在解决问题翻阅它试图找到合适方案时，尽可能选择靠前的方法。

---

并查集应用

同集搜索问题（并查集）

        题目示例：HUD1213 How Many Tables

                          POJ2524 Ubiquitous Religions

        仍然让我们从最简单最基础的部分开始，尽管也许你觉得这已经so easy了，但相信我，最基础的永远是核心。当你最开始接触并查集，解决的第一个问题就应该是它——同集搜索！即单纯地告诉你成对的相等关系，最终让你找到一共有多少组集合，或者搜索两个成员是否在同一个集合当中。比如输入A=B , B=C，你就应该得到A=C，这是一个简单并查集就能做到的事情，甚至不需要额外的操作，但仍然让我们严肃对待它。使用下面的模板，可以解决这个问题。

int maxn;
int a[maxn];
int main(){
    int n;
    cin>>n;
    Init(n);
    while(n--){
        cin>>x>>y;
        Merge(x,y);
    }
    find();
}    

异集搜索问题（并查集）

        题目示例：POJ1703 Find them,Catch them

                          POJ2492 A Bug's Life

        当题目中只有两个集合，且只提供不相等关系时，不相等的跳跃传递性使得简单并查集不可以直接判断。例如A≠B，B≠C，则A=C，不难发现由≠链接起来的关系链，每一项和它的后第二项是相等的，想明白这个逻辑，这种“要么A，要么B”的问题变得简单了，用秩来解决这个问题：

bool RankFind(int x, int y){
    if(abs(rank[x] - rank[y]) % 2 == 0)    return 1;//同
    if(abs(rank[x] - rank[y]) % 2 != 0)    return 0;//异
}
int main(){
    int n;
    cin>>n;
    RankInit(n);
    while(n--){
        int x, y;
        cin>>x>>y;
        RankMerge(x,y);
    }
    bool f = RankFind();
}

多接口（并查集+struct）

        题目示例：HDU3635 Dragon Balls

        并查集并不是只能储存一个简单的数字来标记父节点的位置，事实上往往不止如此。我们可以用结构体（这很常见）赋予并查集更多的接口，来储存更多的信息。这很简单，但是不得不提一下以免被遗忘，同时这有助于我们开启下面的部分。

无向图（并查集+vector）

        题目示例：HDU2586 How far away

        在传统的并查集中，节点之间的连接是隐含方向性的（从子到父），但在无向图问题中，点之间是可以互相到达的，如果把它们放到树里面，它们在树中的秩将是混乱矛盾的，所以不再是树状结构，而是一张图。图中的节点没有父子关系，我们可以以一个节点为主，将其余连接它的节点称为“兄弟节点”。

        用并查集维护无向图的逻辑是：对于节点p[x]，x是当前节点的标号，p[x]储存了x的所有兄弟节点的标号，由于这些兄弟节点的数量往往是不可知的，所以用vector来实现它，因此p实际上是vector的数组。

int maxn = 10;
vector b[maxn];
void Init(int n){
	for(int i=1;i<=n;i++){
		b[i].clear();	
	}
}
int main(){
	int n；
	cin>>n;
	Init(n);
	while(n--){
		int x, y;
		cin>>p>>q>>d;
		b[x].push_back(y);	
		b[y].push_back(x);
    }
}

        需要注意的是，对于无向图并查集进行“并”和”查“操作时，不能忘了需要将整个节点的vector内容进行遍历，不然也是非法的。

        如果因为一些原因不使用vector，也可以使用二维数组，动态数组甚至是链表来模拟vector。

最近公共祖先LCA-Tarjan算法（并查集）

        题目示例：HDU2586 How far away

        Tarjan算法是基于并查集实现求解LCA问题的算法，其具体的理解和逻辑会在另一篇LCA笔记最近公共祖先LCA学习笔记-朴素、倍增和Tarjan_ex_voda的博客-CSDN博客中专门讲解，此处只放代码实现模板。

#include<bits/stdc++.h>
using namespace std; 

const int maxn = 1000;
struct node{
    int parent;        //父节点
    vector<int> son;    //子节点
    vector<int> question;	//查询关系节点 
}p[maxn];   	//树 
int a[maxn];     //并查集，用于合并节点 
bool vis[maxn] = {false};
map<string,int> ans;	//储存查询结果 
queue<string> que;	//储存查询条目
string Com(int x, int y){
	string strx, stry;
	stringstream sx, sy;
	sx<<x;	sy<<y;
	sx>>strx;	sy>>stry;
	return strx+","+stry;
}
void Init(int n){        //初始化
    for(int i=1;i<=n;i++){
    	a[i] = i;
        p[i].parent = i;
        p[i].son.clear();
    }
}
int Find(int x){		//这个Find找的是并查集的根节点 
	if(x==a[x])	return x;
	else return Find(a[x]);
} 
void Tarjan(int x){
	for(int i=0;i<p[x].son.size();i++){
		Tarjan(p[x].son[i]);		//找到最深的子节点 
		a[p[x].son[i]] = x;			//回溯，将子节点合并到当前节点 
		vis[p[x].son[i]] = true;	//记录合并过了 
	}	//离开循环，说明没有子节点或子节点已经遍历完了，开始处理当前节点的查询
	for(int i=0;i<p[x].question.size();i++){	//循环开始，说明有查询内容 
		if(vis[p[x].question[i]]){	//如果合并过了
			ans[Com(p[x].question[i],x)] = Find(p[x].question[i]);
			ans[Com(x,p[x].question[i])] = Find(p[x].question[i]);
			//1,2和2,1的LCA是一回事，都存一下 
		}
	} 
}
int main(){
    int n, m;
    cin>>n>>m;
	Init(n);
    int x, y;
    while(m--){        //输入树
        cin>>x>>y;        //这里不特别讨论x=y的情况了，看具体题目
        p[y].parent = x;
        p[x].son.push_back(y);
    }
    int q;
    cin>>q;
    while(q--){       //查询
    	cin>>x>>y;
		p[y].question.push_back(x);
		p[x].question.push_back(y);
		que.push(Com(x,y));
	}
	int x_i = x;
	while(x_i!=p[x_i].parent)	x_i = p[x_i].parent;	//找到树根节点 
	Tarjan(x_i);
	while(!que.empty()){
		cout<<ans[que.front()]<<endl;		//按查询条目输出查询结果 
		que.pop();
	}
}

复杂关系链（并查集）

        题目示例：POJ1182 食物链

        所谓的复杂关系链，指的是关系传递长度＞2，即不再是等或不等的简单问题，而是A->B,B->C,C->D,的链式传递，甚至可以是环式的。当节点甚至是集合之间的关系变得复杂、冗长，我们不得不需要重新审视并强调并查集的核心思想（尽管在此之前我们都可以在一定程度上忽略）——维护节点和集合之间的关系。并查集所储存的内容本质上是一种关系，就像我们之前提到的父子关系和兄弟关系一样，当它们变得复杂，不再局限于两个节点和两个集合之间，就不得不铭记这一点。

        当然，如何具体地去实现关系的储存和操作，并使得整个过程变得简单，是一门应题而异的学问，但我们可以做一些总结。

（1）平铺错位法

        如果关系的数量是已知且少量的，可以采用平铺错位法，这个思想参考了Jerry233对poj1128的解题方法，具体可见POJ - 1182： 食物链 （并查集）_Jerry233的博客-CSDN博客_poj1182

        这是一种相对简单的方法，将难度隐藏在逻辑假设而不是程序算法上，简单来说便是赋予一个节点多个接口作为定位点，而两个节点之间定位点的错位情况作为关系的辨别方法，我很喜欢这种类似信号的处理手法。这在时间上几乎都是最优的，它充分利用了并查集单独操作节点的特性，而不需要任何的遍历或者递归。但是我不确定它是否具有普适性，另外如果关系链较复杂，在空间上会占据（关系数*节点数）的量。

int main(){
    if(){
        MergeFind(x,y)
        MergeFInd(x+n,y+n)
        MergeFInd(x+2*n,y+2*n)
        .
        .
        .
        MergeFind(x+(T-1)*n,y+(T-1)*n)        //T是关系数
    }
    if(){
        MergeFind(x,y+n)
        MergeFInd(x+n,y+2*n)
        MergeFInd(x+2*n,y+3*n)
        .
        .
        .
        MergeFind(x+(T-1)*n,y)        //T是关系数
    }
    .
    .
    .
}

（2）LCA法

        我们仍然可以用树来储存关系链，这实际上是对异集搜索问题中所用的方法的一个衍生：对于已知关系数量的链，我们可以根据当前两个节点到它们最近公共祖先节点的高度的差的余数来判断它们的关系(abs（deep[x] - deep[y]）%n)，LCA法的核心在于：找到祖先节点，同时记录高度的差异。这事实上是一种过度方法，简单来说我们把平铺错位法的一维链拉开了变成了一棵树，但是它不对路径进行压缩，这意味着你需要遍历这个树，这个方法在空间和时间上都不聪明，但是它十分简单并且便于理解。

        注：求LCA的方法已经在前文给出，如果你还想查阅更多的内容，请看另一篇LCA笔记最近公共祖先LCA学习笔记-朴素、倍增和Tarjan_ex_voda的博客-CSDN博客

int main(){
    int lca;
    if(p[x].deep>p[y].deep)    swap(x,y);
    lca = LCA(y,x);
    int del = p[y].deep + p[x].deep - 2*p[lca];
    del /= T        //T是周期数
    //判断del
}

（3）向量法

        更自然地，我们可以直接把代表关系的域建立在并查集节点内，这使得程序的创建思路更可读，但关系链在路径压缩的过程中需要被同步更新，我们需要一个统一的逻辑来处理所有的类似的问题。向量法参考了

​​​​​​飘过的小牛对poj1128的解题方法，具体可见POJ-1182 食物链_飘过的小牛的博客-CSDN博客。

        这个方法的建立更自然，更朴实，但实现更困难，我们来结构性地总结一下：事实上所谓的向量体现在节点关系的传递方式特点上——假设x_i是x的根节点，y_i是y的根节点，输入x和y的关系，试图找到x_i和y_i的关系，可以扩展为：x_i->y_i = x_i->x + x->y + y->y_i。

        因此向量法是对秩法的一个优化，维护关系的核心逻辑是一样的，只是完成了路径压缩使得算法效率更优，为了方便查阅，我们给出向量法的函数模板。

int maxn;
struct node
{
	int pre;
	int relation;
};
node p[maxn];
void VInit(int n){        //初始化
    for(int i = 1; i <= n; ++i) 
	{
		p[i].pre = i;
		p[i].relation = 0;
	}
}
int VFind(int x) //查找根结点
{
	int temp;
	if(x == p[x].pre)
		return x;
	temp = p[x].pre; //路径压缩
	p[x].pre = find(temp);
	p[x].relation = (p[x].relation + p[temp].relation) % T; //关系域更新 ,T代表关系周期数，  
	return p[x].pre; //根结点
}
void VMerge(int x, int y){
    int x_i = VFind(x);
    int y_i = VFind(y);
    if(x_i != y_i) // 合并
		{
			p[y_i].pre = x_i;
			p[y_i].relation = (3 + (rel - 1) +p[x].relation - p[y].relation) % T;
		}        //rel代表关系标号,T代表关系周期数 , 如果没有周期，则不%

}