51Nod－1050－循环数组最大子段和

ACM模版

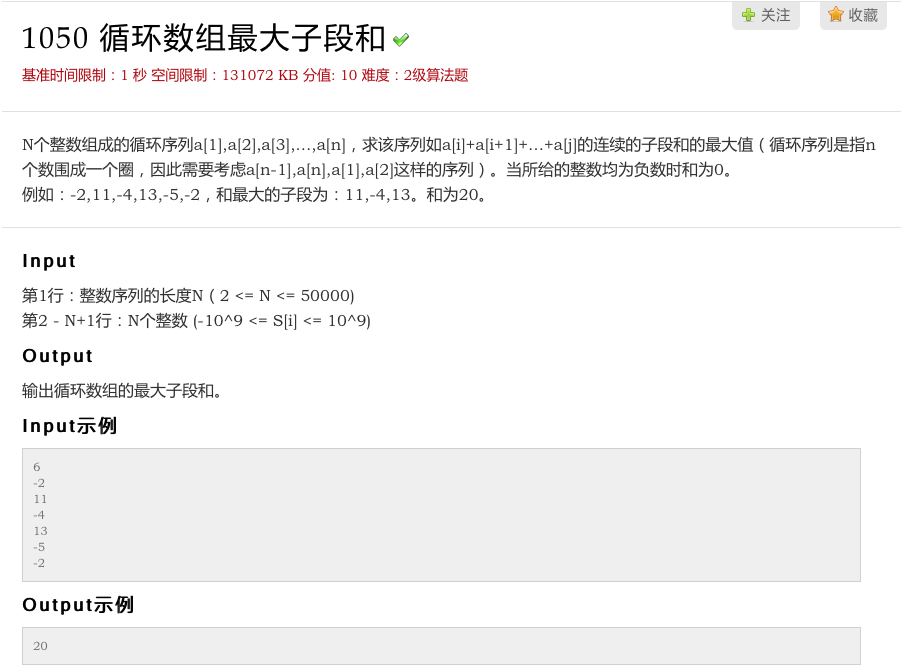
描述

题解

这里分为两种情况：
其一：从[1, n]的正常顺序的最大子段和；
其二：从开头取一部分，结尾取一部分，中间舍去，那么中间的一定是最小子段和，然后所有数据的和减去最小子段和即可。
最后从两种情况中选取相对较大的情况。

代码

#include <iostream>
#include <cstdio>

using namespace std;

typedef long long ll;

const int MAXN = 5e4 + 10;

ll A[MAXN];
ll All[MAXN], Start[MAXN];

ll MaxSubStringOne(ll *A, int n)
{
    int i;
    Start[n - 1] = A[n - 1];
    All[n - 1] = A[n - 1];
    for(i = n - 2; i >= 0; i--)         //  根据题意，从后向前遍历，反之亦可。
    {
        Start[i] = max(A[i], (A[i] + Start[i + 1]));
        All[i] = max(Start[i], All[i + 1]);
    }
    return All[0];                      //  All[0] 中存放结果
}

ll MaxSubStringTwo(ll *A, int n, ll sum)
{
    int i;
    Start[n - 1] = A[n - 1];
    All[n - 1] = A[n - 1];
    for(i = n - 2; i >= 0; i--)         //  根据题意，从后向前遍历，反之亦可。
    {
        Start[i] = min(A[i], (A[i] + Start[i + 1]));
        All[i] = min(Start[i], All[i + 1]);
    }
    return sum - All[0];                //  All[0] 中存放结果
}

int main(int argc, const char * argv[])
{
    int N;
    cin >> N;
    ll sum = 0;
    for (int i = 0; i < N; i++)
    {
        scanf("%lld", A + i);
        sum += A[i];
    }
    ll ans_1 = MaxSubStringOne(A, N);
    ll ans_2 = MaxSubStringTwo(A, N, sum);
    cout << (ans_1 > ans_2 ? ans_1 : ans_2) << '\n';
    return 0;
}

参考

51Nod－1049－最大子段和