根据buffon的针的概率算法,只要在地板上大约落下150万根针,每100次中就有95次可以将pi的值估计到0.01内,落下的针的长度是地板上的木板宽度的一半。以n/k作为对pi的估计。其中n 是落下的针数,k 是与木板之间的缝隙相交的针数。请说明可以通过落下两倍长的针来改进这个算法,并且以n/2k作为对pi的估计。如果有至少95%的概率得到pi的估计值误差在0.01内,需要多少根针?
解:
1、每根针有两个要素:针的中点的位置,以及针的偏角,一旦这两个因素确定了,则针的位置也就确定了。
2、设木地板宽度为a,针的长度就是l=a/2,则针的中点到其下方的最近一个缝隙的距离x在(0, a/2]上均匀分布,而角度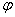 在(0, π]上均匀分布。
在(0, π]上均匀分布。
样本空间为
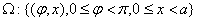
针与平行线相交的充要条件是
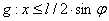
(见图1).
所求概率是
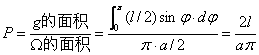
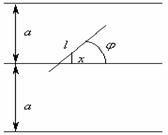
图1
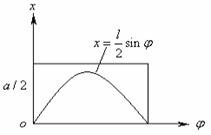
图2
3、多次抛针,而每次抛针时的条件都是相同的,则每次抛针时与地板缝隙相交的概率都是p,则这就是一个典型的伯努利实验,得到的结果就满足二项分布
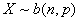 ,即设总共抛针n次,出现k次相交的概率为
,即设总共抛针n次,出现k次相交的概率为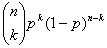 。根据De Moivre-Laplace中心极限定理,可得随机变量
。根据De Moivre-Laplace中心极限定理,可得随机变量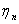 服从参数为n,p的二项分布,则对于任意的x有:
服从参数为n,p的二项分布,则对于任意的x有:
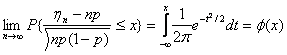 ,
,
其中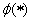 为标准高斯分布的累积函数。
为标准高斯分布的累积函数。
并且将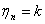 带入到上式中去,可以得到:
带入到上式中去,可以得到:

在n/k 作为pi的估计不超过0.01的情况下,可以得到
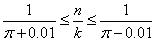
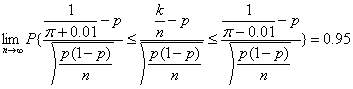
通过查阅标准高斯分布累积函数表可得
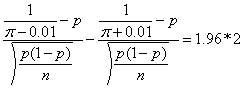
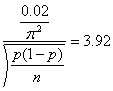
当针的长度为木板长度的一半时,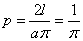 ,并将其代入上式,可得
,并将其代入上式,可得
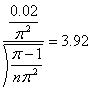
可以求得
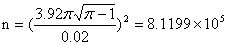
当针的长度等于木板的长度时,

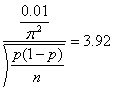
将
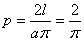 代入,得
代入,得
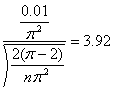
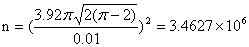
























 194
194

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








