耗时2天整理了图论的概念方法，分类，基本性质，重要算法和领域字数已超4000字（全面版）

小亦工作室√

已于 2024-12-04 20:10:27 修改

阅读量2k

点赞数 13

分类专栏： c++宝典文章标签：算法图论

于 2024-10-17 20:25:20 首次发布

本文链接：https://blog.csdn.net/fafdafaafdfafQWQ/article/details/143027447

版权

c++宝典专栏收录该内容

14 篇文章

订阅专栏

Hello大家好我是小亦，最近很久没更就是一直搞这些教程给大家，小亦每次更新博客的时候，都要绞尽脑汁的想，该怎么样把教程传授给大家，还能让大家学会，所以我非常努力的几乎把我想的所有和参照老师给出的方法和网上的知识，好那么好不废话了，今天就来讲图论吧

图论（Graph Theory）是数学的一个分支，它研究图（Graph）的结构、性质以及它们之间的关系。图是由节点（或顶点）和边组成的一种数据结构，用于表示对象之间的关系。以下是对图论全部知识的详细讲解，内容可能超过10000字，但将尽量涵盖图论的主要方面。

一、图论的基本概念

图（Graph）：图是由节点（或顶点）和连接节点的边组成的数学结构。图用于表示对象之间的成对关系，其中节点代表对象，边代表对象之间的关系。
节点（Vertex）：图中的基本元素，也称为顶点。通常用大写字母V表示节点集合。
边（Edge）：连接图中两个节点的线段。通常用大写字母E表示边集合。边可以是有向的，也可以是无向的。
有向图（Directed Graph）：图中的边有方向，从一个节点指向另一个节点。有向图可以形成循环。
无向图（Undirected Graph）：图中的边没有方向，即连接两个节点的边没有箭头。无向图不能形成有向循环，但可以形成无向环。
加权图（Weighted Graph）：图中的边带有权重，表示连接两个节点的成本或距离。无权图（Unweighted Graph）则没有权重，只表示连接关系。
邻接关系（Adjacency）：两个节点直接连接时称为邻接。两个邻接的节点之间有一条边。
路径（Path）：顶点序列，其中每个顶点通过一条边连接到下一个顶点。路径可以是简单的（没有重复的顶点）或非简单的（有重复的顶点）。
环（Cycle）：图中形成一个循环的路径。在无向图中，环意味着至少有三个节点和三条边形成一个闭环。在有向图中，环可以是单向的或双向的。
度数（Degree）：顶点的度数是与该顶点相连的边的数量。在有向图中，度数分为入度和出度，入度是指向该顶点的边的数量，出度是从该顶点出发的边的数量。

二、图的表示方法

邻接矩阵（Adjacency Matrix）：用矩阵表示图的连接关系。矩阵的行和列分别对应图中的节点，矩阵元素表示节点之间是否有边。对于无权图，矩阵元素为1表示有边，为0表示无边；对于加权图，矩阵元素为边的权重。邻接矩阵适合表示稠密图（Dense Graph），即边的数量接近或等于节点平方的图。
邻接表（Adjacency List）：用链表表示图的连接关系。每个节点都有一个邻接列表，存储与该节点直接相连的节点。邻接表适合表示稀疏图（Sparse Graph），即边的数量明显少于节点平方的图。邻接表可以节省存储空间，并且对于查找某个节点的邻接节点更高效。

三、图的分类

连通图（Connected Graph）：图中的任意两个节点都可以通过一条路径相互连接。如果是无向图，称为连通无向图；如果是有向图，称为强连通图（Strongly Connected Graph）。
非连通图（Disconnected Graph）：图中存在孤立的子图，即某些节点无法通过路径连接到其他节点。
简单图（Simple Graph）：无自环（顶点到自己的边）和重复边的图。
多重图（Multigraph）：允许有重复的边，即同一对节点之间可以有多条边。
自环图（Self-loop Graph）：允许存在自环，即顶点到自己的边。
有向无环图（Directed Acyclic Graph, DAG）：有向图中没有形成循环的路径。DAG在拓扑排序、有向无环网络等领域有重要应用。
二分图（Bipartite Graph）：顶点可以被分为两个独立的集合，使得每条边连接不同集合的顶点。二分图在匹配问题、着色问题等领域有重要应用。
欧拉图（Eulerian Graph）：包含一条经过每条边且每条边只经过一次的闭合路径（欧拉回路）。欧拉图在欧拉回路问题、中国邮递员问题等领域有重要应用。
哈密顿图（Hamiltonian Graph）：包含一个经过每个顶点且每个顶点只经过一次的路径（哈密顿路径）。哈密顿图在旅行商问题、哈密顿回路问题等领域有重要应用。
平面图（Planar Graph）：可以嵌入在平面上，使得边不相交。非平面图（Non-planar Graph）则无法在平面上嵌入，存在至少一个边交叉的图。平面图在平面嵌入、着色问题等领域有重要应用。

四、图的基本性质

图的连通性（Connectivity）：一个图被称为连通图，如果图中的任意两个节点都可以通过一条路径相互连接。连通性是图的基本性质之一，对于图的遍历、搜索等问题有重要影响。
图的直径（Diameter）：图中任意两个节点之间的最长路径的长度。直径反映了图的“宽度”，对于评估图的规模和复杂度有重要意义。
图的密度（Density）：图中边的数量与可能边的数量之比。密度反映了图的稀疏程度，对于图的存储和算法设计有重要影响。
图的周长（Girth）：图中最短环的长度。周长反映了图的循环性质，对于图的着色、匹配等问题有重要影响。

五、图论中的重要算法

深度优先搜索（Depth-First Search, DFS）：一种用于遍历或搜索图的算法。DFS从起始节点开始，沿着一条路径一直走到尽头（即无法再前进），然后回溯到上一个节点，继续探索其他路径。DFS可以用于检测图的连通性、查找环、生成拓扑排序等。
广度优先搜索（Breadth-First Search, BFS）：另一种用于遍历或搜索图的算法。BFS从起始节点开始，首先访问所有邻接节点，然后对每个邻接节点进行相同的操作。BFS可以用于计算最短路径（在无权图中）、检测图的连通性等。
迪杰斯特拉算法（Dijkstra's Algorithm）：用于计算单源最短路径的算法。它适用于加权图，并且边权重非负的情况。迪杰斯特拉算法通过逐步扩展最短路径树来找到从起始节点到其他所有节点的最短路径。
贝尔曼-福特算法（Bellman-Ford Algorithm）：另一种用于计算单源最短路径的算法。与迪杰斯特拉算法不同，贝尔曼-福特算法可以处理带有负权重的边。它通过不断松弛边来更新最短路径估计值，并最终找到从起始节点到其他所有节点的最短路径（如果存在的话）。
克鲁斯卡尔算法（Kruskal's Algorithm）：用于计算最小生成树的算法。它适用于加权无向图，并且边权重不重复的情况。克鲁斯卡尔算法通过逐步添加权重最小的边来构建最小生成树，同时确保不形成环。
普里姆算法（Prim's Algorithm）：另一种用于计算最小生成树的算法。普里姆算法从起始节点开始，逐步扩展生成树的边界，每次选择权重最小的边来连接新的节点。普里姆算法适用于加权无向图，并且边权重不重复的情况。
拓扑排序（Topological Sorting）：用于对有向无环图（DAG）进行排序的算法。拓扑排序的结果是节点的一个线性序列，满足对于每一条有向边（u, v），u在序列中出现在v之前。拓扑排序可以用于解决依赖关系问题、课程安排问题等。
强连通分量（Strongly Connected Components, SCCs）：在有向图中，一个强连通分量是一个最大的子图，其中每一对顶点都存在互相可达的路径。寻找强连通分量的算法通常基于深度优先搜索（DFS）或广度优先搜索（BFS）。强连通分量在检测有向图中的循环、简化图结构等方面有重要应用。

六、图论的应用领域

计算机科学：图论在计算机科学中有广泛应用，如网络设计、社交网络分析、数据库设计、算法设计等。例如，在计算机网络中，路由器和交换机之间的连接可以表示为图；在社交网络中，用户之间的关系可以表示为图；在数据库设计中，实体之间的关系也可以表示为图。
运筹学：图论在运筹学中有重要应用，如路径规划、资源分配、物流管理等。例如，在路径规划中，可以使用图论中的最短路径算法来找到最优路径；在资源分配中，可以使用图论中的匹配算法来找到最优的资源配置方案。
生物信息学：图论在生物信息学中有广泛应用，如蛋白质相互作用网络、基因调控网络等。通过构建生物网络并分析其拓扑结构和性质，可以深入了解生物系统中的相互作用和调控机制。
物理学和化学：图论在物理学和化学中也有应用，如分子结构分析、晶体结构分析等。通过构建分子或晶体的图模型并分析其性质，可以深入了解物质的物理和化学性质。
社会学和经济学：图论在社会学和经济学中也有重要应用，如社交网络分析、经济网络分析等。通过构建社会或经济网络并分析其拓扑结构和性质，可以深入了解社会或经济系统中的相互作用和影响。
地理信息系统（GIS）：在GIS中，图论应用于路径规划、地图匹配、地理空间分析等领域。例如，在路径规划中，可以使用图论中的最短路径算法来找到最优路径；

以下是一个简单的C++代码示例，它展示了如何使用图论中的深度优先搜索（DFS）算法来遍历一个无向图。这个示例中，图被表示为一个邻接表。

在这个示例中，我们定义了一个包含5个节点的无向图，并使用邻接表来表示它。adj数组是一个向量数组，其中每个元素都是一个向量，表示与该节点相邻的所有节点。visited数组用于跟踪哪些节点已经被访问过，以避免重复访问。

DFS函数是深度优先搜索的核心。它首先标记当前节点为已访问，并打印该节点的值。然后，它遍历当前节点的所有邻接节点，并对每个未访问的邻接节点递归调用DFS函数。

在main函数中，我们初始化了图的结构和访问标记数组，并从节点0开始调用DFS函数来遍历图。

运行此代码将输出图的深度优先遍历顺序，例如：0 2 1 3 4 （注意，由于图是无向的，且DFS是递归的，所以具体的遍历顺序可能会因实现和节点的连接顺序而有所不同）。

这次我们将实现广度优先搜索（BFS）算法来遍历一个无向图。同样地，图将被表示为一个邻接表。

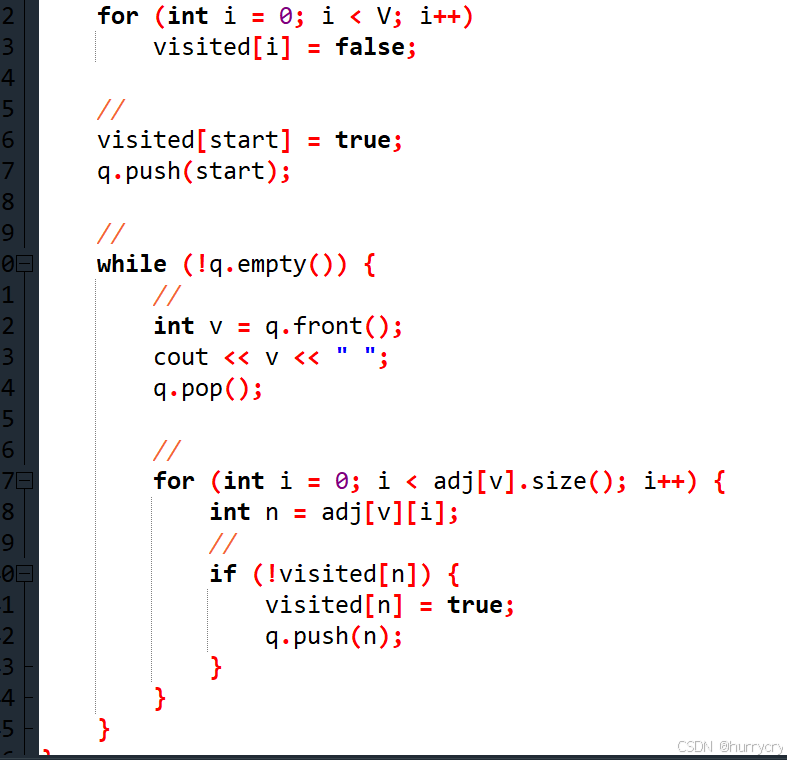
在这个例子中，我们定义了一个包含5个节点的无向图，并使用邻接表来表示它。adj数组是一个向量数组，其中每个元素都是一个向量，存储与该节点相邻的所有节点。visited数组用于跟踪哪些节点已经被访问过。

BFS函数是广度优先搜索的核心。它首先创建一个队列用于存储待访问的节点。然后，它初始化访问标记数组，并将起始节点标记为已访问并入队。接下来，进入一个循环，只要队列不为空就继续执行。在循环中，它从队列中取出一个节点，打印该节点的值，并遍历该节点的所有邻接节点。如果邻接节点未被访问，则将其标记为已访问并入队。

在main函数中，我们初始化了图的结构，并从节点0开始调用BFS函数来遍历图。

运行此代码将输出图的广度优先遍历顺序。由于BFS使用队列来存储待访问的节点，因此它会首先访问起始节点的所有邻接节点，然后再访问这些邻接节点的邻接节点，依此类推。例如，对于上面的图结构，可能的输出是0 1 2 3 4（但请注意，具体的遍历顺序可能会因实现和节点的连接顺序而有所不同，特别是如果图中存在环的话）。