今天要学习的主要是odeint函数,Scipy.integrate模块的odeint函数是lsoda的Fortran代码的Python封装。
首先来了解一下理论背景:
如果说,我们要对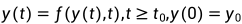 进行数值求解,我们就需要一个函数
进行数值求解,我们就需要一个函数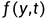 来计算,其右侧返回一个和y相同形状的数组,还需要一个包含初始值的数组y0,以及一个tvals和一个独立变量t值数组,希望返回相应的y值,那么,这时我们要通过这样的方式来返回y的近似解:
来计算,其右侧返回一个和y相同形状的数组,还需要一个包含初始值的数组y0,以及一个tvals和一个独立变量t值数组,希望返回相应的y值,那么,这时我们要通过这样的方式来返回y的近似解:
y=odeint(f,y0,tvals)第一个问题:我们要使用什么样的步长h?他和tvals有什么关系嘞?
答:每个点选择的步长h都受到了保持精度需求的约束,这就出现了我们怎么样去确定精度的问题,函数odeint他就是试着估计局部误差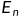 那么,就定义绝对误差为
那么,就定义绝对误差为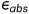 的最小值,同时要求:
的最小值,同时要求: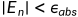 ,同时相应的调整步长就好,但是,如果说
,同时相应的调整步长就好,但是,如果说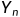 变得非常大的话,上面的不等式准则可能会使得我们所选取的步长h变得非常小,也非常低效,那么,我们在定义相对误差
变得非常大的话,上面的不等式准则可能会使得我们所选取的步长h变得非常小,也非常低效,那么,我们在定义相对误差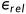 ,要求:
,要求: ,但是,这个方法在
,但是,这个方法在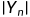 变小的情况下可能会出现问题,所以,通常的准则是:
变小的情况下可能会出现问题,所以,通常的准则是: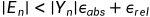 ,
,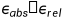 ,是数组,两个默认值是
,是数组,两个默认值是 。
。
odient是可以自动处理刚性问题的方程,或者是方程组。
先跟着书上的学着写一个:
谐波振荡器:
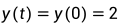
假社,我们希望在t=1处求解:
import numpy as np
from scipy.integrate import odeint
print(odeint(lambda y,t:y,1,[0,1]))看一看输出的结果:
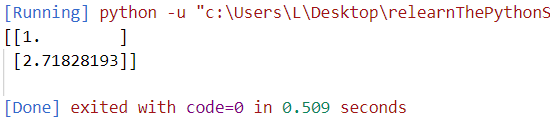
图1:输出结果
lambda是匿名函数,f作为第一个参数,第二个参数是初始的y值,第三个参数是由强制的初始t值和最终y值组成的列表,这个列表被隐式转换为浮点数的numpy数组,输出由t数值和y数组构成,并且省略了初值。
这里,我们做一个简谐运动的问题:
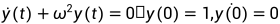
对上面的方程,我们给他改成一个方程组:
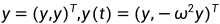
在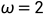 以及
以及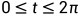 的范围内进行求解和绘图:
的范围内进行求解和绘图:
import numpy as np
from scipy.integrate import odeint
# print(odeint(lambda y,t:y,1,[0,1]))
import matplotlib.pyplot as plt
def rhs(Y,t,omega):
y,ydot=Y
# 为了返回值的清晰,在这里展开了向量参数
return ydot, -omega**2*y
#返回了一个元组,而且这个元组被转换成了数组
t_arr=np.linspace(0,2*np.pi,101)
y_init=[1,0]
omega=2.0
#他这里的传参好怪啊
y_arr=odeint(rhs,y_init,t_arr,args=(omega,))
# args的参数必须是元组,输出被打包成了一个二维数组
y,ydot=y_arr[:,0],y_arr[:,1]
# 解包这个二维数组
fig=plt.figure()
ax1=fig.add_subplot(1,2,1)
ax1.plot(t_arr,y,t_arr,ydot)
ax1.set_xlabel("t")
ax1.set_ylabel("Y and ydot")
ax2=fig.add_subplot(1,2,2)
ax2.plot(y,ydot)
ax2.set_xlabel("y")
ax2.set_ylabel("ydot")
plt.tight_layout()
fig.subplots_adjust(top=0.9)
plt.show()
图2:简谐运动
如果我们继续对上面的代码进行修改,在相空间中创建网格并且绘制方向场,就是网格中的每个点的向量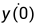 ,然后从图形的任意点(任意初始条件)开始绘制解函数:
,然后从图形的任意点(任意初始条件)开始绘制解函数:
fig=plt.figure()
y,ydot=np.mgrid[-3:3:21j,-6:6:21j]
u,v=rhs(np.array([y,ydot]),0.0,omega)
mag=np.hypot(u,v)
mag[mag==0]=1.0
plt.quiver(y,ydot,u/mag,v/mag,color="red")
print("\nUse mouse to select number of trajectories")
print("time out after 30 seconds")
choice=[(0,0)]
while len(choice)>0:
y01=np.array([choice[0][0],choice[0][1]])
y=odeint(rhs,y01,t_arr,args=(omega,))
plt.plot(y[:,0],y[:,1],lw=2)
choice=plt.ginput()
print("timeout!")
图三
说实话,书上的这个代码我是没怎么看懂的,他的意思是说,选择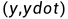 坐标来覆盖相空间中相对粗糙的网格,计算网格中每个点切线向量场的分量
坐标来覆盖相空间中相对粗糙的网格,计算网格中每个点切线向量场的分量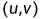 ,然后用quiver绘制小箭头,大小和方向是向量场的,基点是网格端,在u=v=0(平衡点附近),箭头最终成为了无信息点,然后就是绘制轨迹。
,然后用quiver绘制小箭头,大小和方向是向量场的,基点是网格端,在u=v=0(平衡点附近),箭头最终成为了无信息点,然后就是绘制轨迹。
呃,说实话,这东西得对着书上的公式一个一个对着看,不然是真的看不懂。
然后我们看一看范德波尔振荡器:
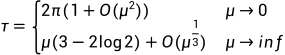
周期轨道的快速弛豫表面这个例子可能会编的刚性,
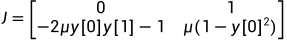
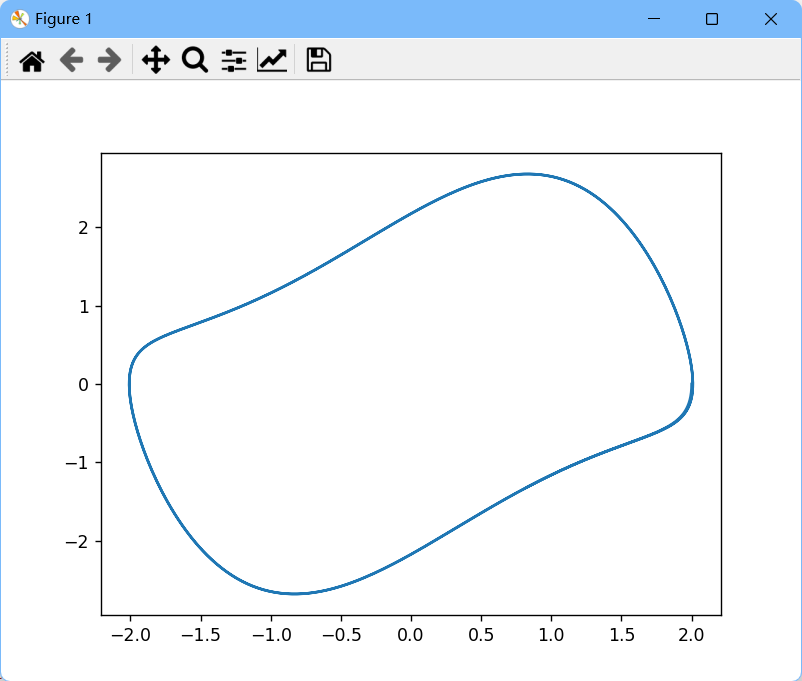
图4:输出结果
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
def rhs(y,t,mu):
return [y[1],mu*(1-y[0]**2)*y[1]-y[0]]
def jac(y,t,mu):
return [[0,1],[-2*mu*y[0]*y[1]-1,mu*(1-y[0]**2)]]
mu=1.0
t_final=15.0 if mu<10 else 4.0*mu
n_points=1001 if mu<10 else 1001*mu
t=np.linspace(0,t_final,n_points)
y0=np.array([2.0,0.0])
#对odeint函数多加了两个参数,第一个告诉积分器在哪里能够找到雅各比函数,第二个是full_output,积分器运行时,他会记录各种统计数据,这些统计数据可以帮助理解积分器到底在干什么
#true就是说。这些数据可以通过info访问,这里通过选择”nje“就是显示雅各比评估数
#针对mu,我们可以试着进行放大,发现,小于15的时候,不用隐式算法,大于15的时候,会需要用到隐式算法
y,info=odeint(rhs,y0,t,args=(mu,),Dfun=jac,full_output=True)
#(我好像大致明白了,rhs、jac这俩函数,应该是隐式的传递参数吧)
print("mu = %g,number of Jacobian calls is %d "%\
(mu,info['nje'][-1]))
plt.plot(y[:,0],y[:,1])
plt.show()他这里的代码有点抽象了,看的不是很懂。
改一改,mu=10的时候看看:
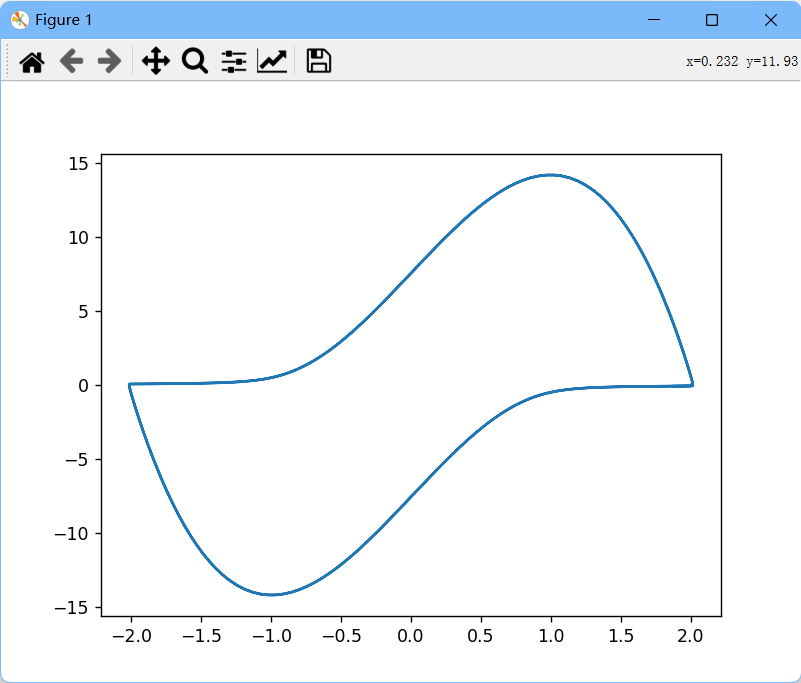
图5:mu=10
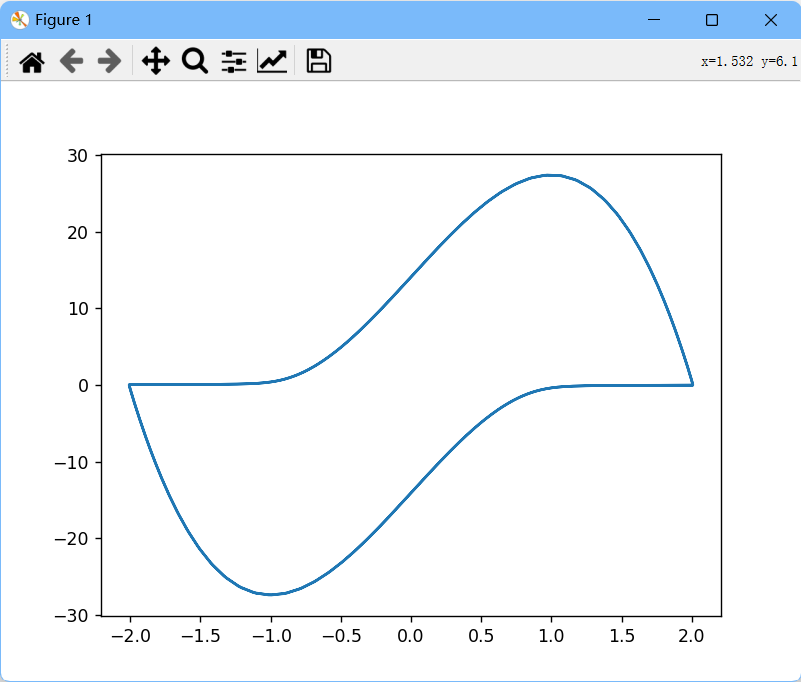
图6:mu=20
增加mu就意味着增加周期。
最后一个,我们来看一看洛伦兹方程,他最早时作为天气模型出现的,表现出混沌行为,:
对于未知数x(t)、y(t)、z(t),方程是:
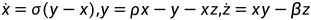
只允许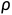 变化,最初研究的是
变化,最初研究的是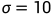 ,
,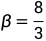 的情况,对于较小的
的情况,对于较小的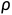 值,是可以预测解的行为的,但是一旦
值,是可以预测解的行为的,但是一旦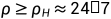 的时候,解就变得非周期性,而且,解对初始条件非常敏感,,稍微不同的两个初始数据对应的解轨迹看起来就非常不同。
的时候,解就变得非周期性,而且,解对初始条件非常敏感,,稍微不同的两个初始数据对应的解轨迹看起来就非常不同。
import numpy as np
from scipy.integrate import odeint
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
def rhs(u,t,beta,rho,sigma):
x,y,z=u
return [sigma*(y-x),rho*x-y-x*z,x*y-beta*z]
sigma=10.0
beta=8.0/3.0
rho1=29.0
rho2=28.8
u01=[1.0,1.0,1.0]
u02=[1.0,1.0,1.0]
t=np.linspace(0.0,50.0,10001)
u1=odeint(rhs,u01,t,args=(beta,rho1,sigma))
u2=odeint(rhs,u02,t,args=(beta,rho2,sigma))
x1,y1,z1=u1[:,0],u1[:,1],u1[:,2]
x2,y2,z2=u2[:,0],u2[:,1],u2[:,2]
# plt.ion()
fig=plt.figure()
ax=fig.add_subplot(1,1,1, projection='3d')
ax.plot(x1,y1,z1,'b-')
ax.plot(x2,y2,z2,'r:')
ax.set_xlabel("x")
ax.set_ylabel("y")
ax.set_zlabel("z")
ax.set_title("Lorenz euqation with rho=%g,%g"%(rho1,rho2))
plt.show()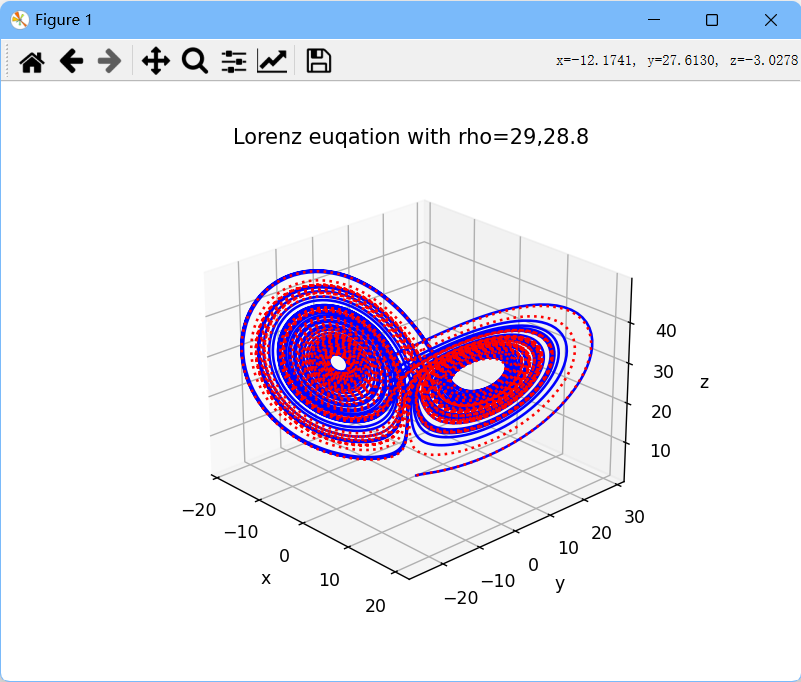
图7
哎,我试试改改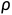 看看:
看看:
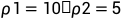 :
:
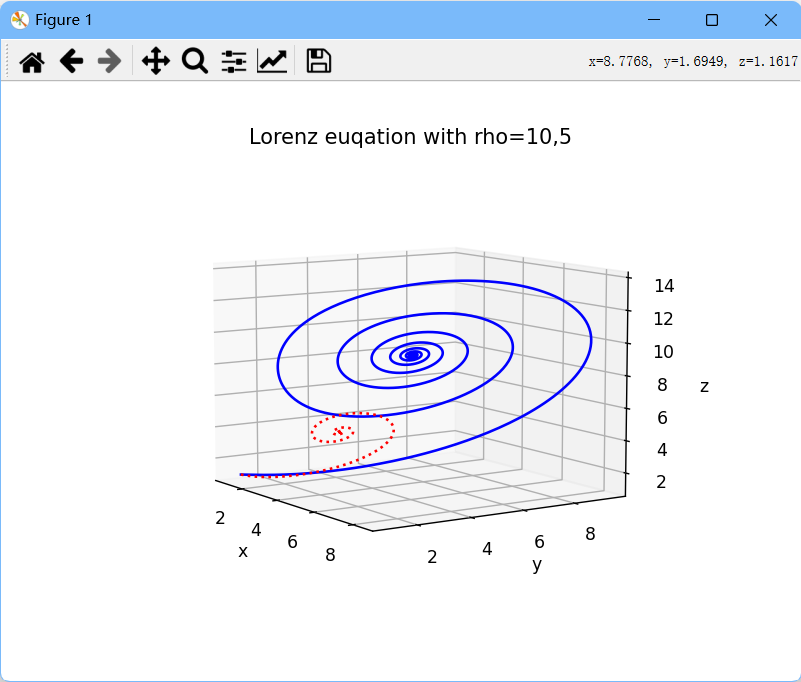
图8:修改参数

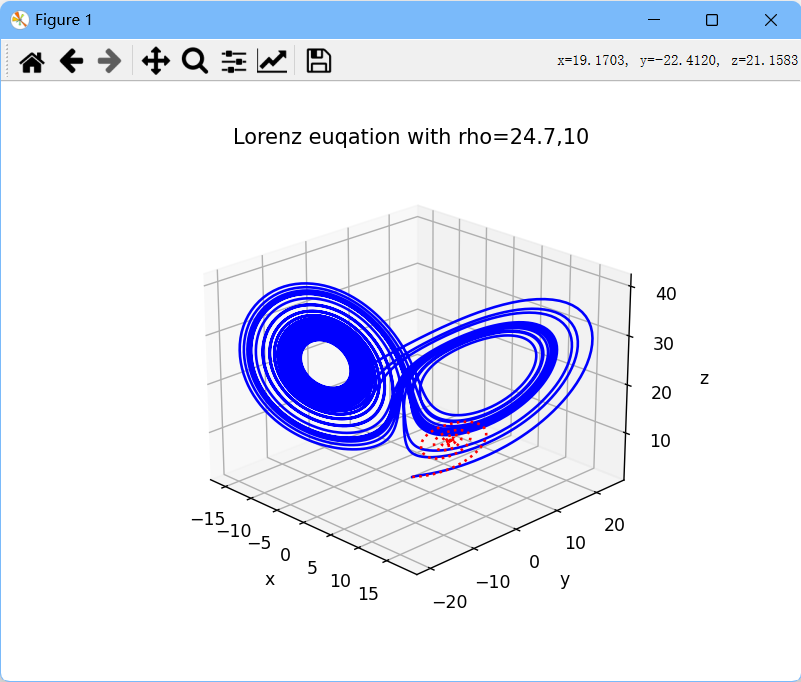
图9
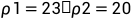 :
:
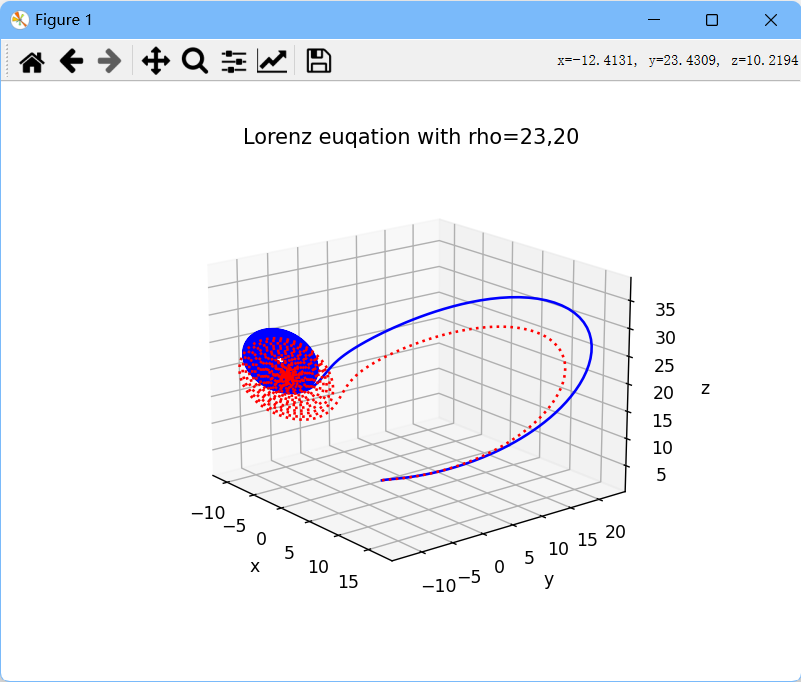
图10
的确,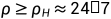 的时候,就变得非周期性,难以预测了。
的时候,就变得非周期性,难以预测了。
如果, ,就会存在平衡点(零速度):
,就会存在平衡点(零速度):
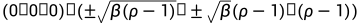
如果说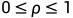 ,只存在唯一一个平衡点:原点,但是似乎在绕着两个非平凡平衡点绕行,从其中的一个平衡点附近,解开始慢慢的螺旋辐射,当半径变得太大时,解跳到另一个平衡点附近,从那里开始进行另一个螺旋辐射,并且过程不断充分,有点像蝴蝶的翅膀。
,只存在唯一一个平衡点:原点,但是似乎在绕着两个非平凡平衡点绕行,从其中的一个平衡点附近,解开始慢慢的螺旋辐射,当半径变得太大时,解跳到另一个平衡点附近,从那里开始进行另一个螺旋辐射,并且过程不断充分,有点像蝴蝶的翅膀。






















 1057
1057











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








