线性代数的一些理解（更新中）

以前学的时候都是囫囵吞枣，能搞过就得了。现在有了点时间可以静下来看看。。

还是分成点来看吧。

1 状态转移方程

以小车运行为例子

一个车匀速在一维坐标前行，速度是2米每秒，起始点是0。如何描述

设 𝑥(𝑡) 表示车辆在时间 𝑡t 时的位置。根据匀速运动的定义，车辆的速度是恒定的，为 2 米每秒。因此，车辆的位置随时间的变化可以用以下线性方程表示：

𝑥(𝑡)=2𝑡

其中，𝑥(𝑡) 表示车辆在时间 𝑡t 时的位置（单位：米），𝑡 表示时间（单位：秒），2𝑡 表示车辆在时间 𝑡t 时已经行驶的距离。

上面是我们常用的理解，在线性代数中，这个应该怎么写呢？

我们可以将位置 𝑥(𝑡)视为一个列向量，时间 𝑡 视为一个标量，速度 𝑣 视为一个常数。

假设时间从 𝑡0 到 𝑡𝑓，我们可以将时间区间分成 𝑁 个离散时间步长。每个时间步长的长度为 Δ𝑡=𝑡𝑓−𝑡0𝑁。

我们可以使用以下线性方程来描述车辆的位置随时间的变化：

𝑥(𝑡𝑖+1)=𝑥(𝑡𝑖)+𝑣Δ𝑡

其中 𝑥(𝑡𝑖)表示车辆在时间 𝑡𝑖ti​ 的位置，𝑥(𝑡𝑖+1) 表示车辆在时间 𝑡𝑖+1​ 的位置，𝑣 表示车辆的速度。

将其转换成矩阵形式：

其中，第一个矩阵是转移矩阵 𝐴，它将 𝑥(𝑡𝑖)映射到 𝑥(𝑡𝑖+1)；第二个矩阵是状态向量，包含了初始位置 𝑥(𝑡0) 和车辆的速度 𝑣。

另外一种写法：

设状态向量为 x=[x,v]T，其中 x 表示位置，v 表示速度。则状态转移方程可以表示为：

其中，xt+1​ 是下一个时刻的状态向量，xt​ 是当前时刻的状态向量，a 是常量加速度。第一个矩阵是状态转移矩阵，描述了状态变量的演变规律；第二个矩阵描述了加速度对状态变量的影响。

观测方程可以根据具体情况来定义，一般形式为 zt​=Hxt​+noise，其中 zt​ 是观测值，H 是观测矩阵，描述了观测如何与状态相关联。

初始状态可以表示为 x0​=[x0​,v0​]T，其中 x0​ 和 v0​ 是初始位置和速度。

还有一种写法是包含加速度：

如果状态向量需要增加加速度，则状态向量的维度需要扩展，同时更新状态转移方程和观测方程。假设状态向量为 x=[x,v,a]T，其中 x 表示位置，v 表示速度，a 表示加速度，则状态转移方程可以表示为：

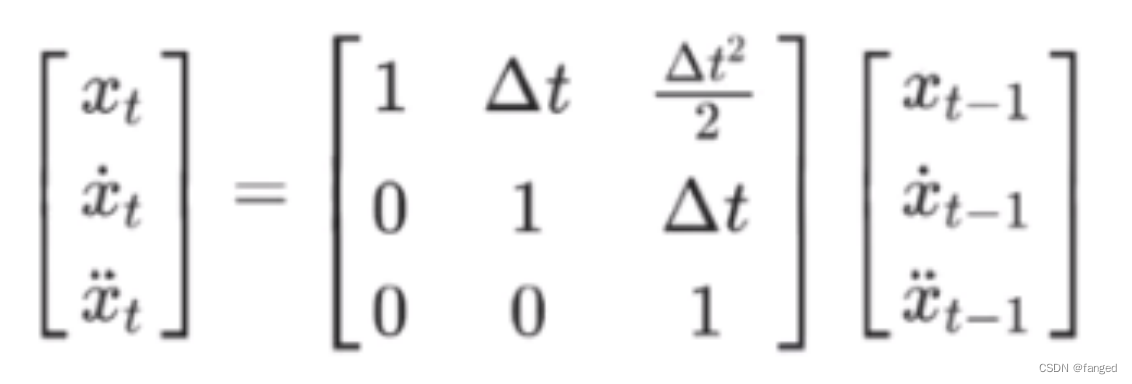
其中xt是初始位置，x一点是速度，x两点是加速度。上面的矩阵，等价于：

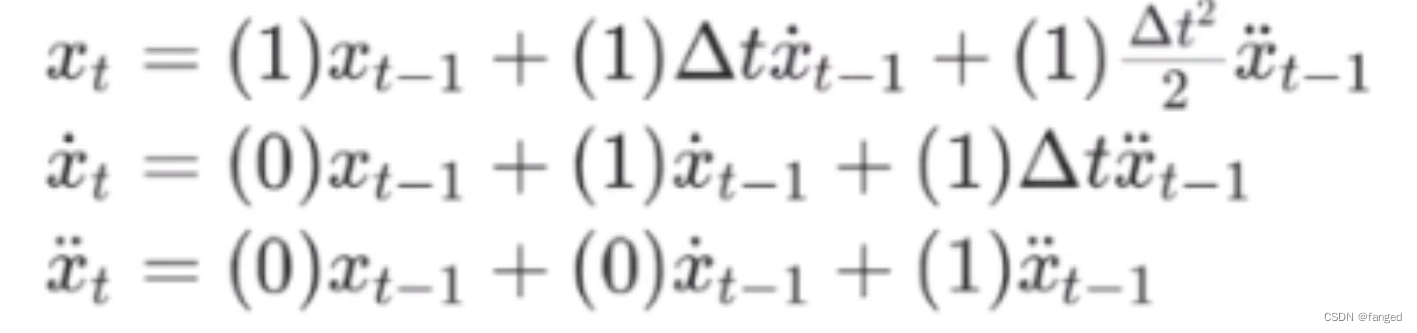
这里再复习一下矩阵乘法。矩阵乘法其实就是方程的另一种表现形式，写成矩阵并不是为了装逼，在计算机中，矩阵乘法可以显著加速运算（算法矩阵提速原理-CSDN博客），所以都写成矩阵模式。个人觉得有些教程还可以先写成方程组的形式，方便理解。

假设我们有一个 2×2 矩阵 A 和一个 2×1 矩阵 B：

我们想要计算它们的乘积 C=A×B。

c1​=(1×5)+(2×6)=5+12=17

c2​=(3×5)+(4×6)=15+24=39

2 协方差矩阵

假设我们有两个随机变量，分别表示一个人的身高和体重。我们想要描述这两个变量之间的关系，我们可以使用一个 2x2 的协方差矩阵来表示。

假设身高的标准差为 10 厘米，体重的标准差为 5 公斤，而身高和体重之间的相关系数为 0.7。

协方差矩阵 P 将如下所示：

身高方差=(身高标准差)平方=10*10=100 平方厘米

体重方差=(体重标准差)平方=5*5=25 平方公斤

身高与体重的协方差=相关系数×(身高标准差)×(体重标准差)=0.7×10×5=35 平方厘米\公斤

因此，协方差矩阵为：