1.8 离散傅里叶变换（DFT）

1.8 离散傅里叶变换（DFT）

• 不论信号的形状如何，大多数实际关心的信号都可以看作是在不同频率下振荡的复正弦波的总和。
• 一组 $N$ 个正交复正弦波可以在 $N$ 个时间域样本的范围内构造。
• 离散频率轴上的每一个“刻度”或“桶”都表示该复正弦波的离散频率 $k/N$。

如图1.35中显示了连续时间方波，该方波是具有不同振幅的正弦波的总和。这样一个方波或矩形信号是一种被称为周期信号的特殊函数，DFT会识别出每个构成频率的幅度，例如1, 1/3, 1/5等，如方程(1.29)所示。现在让我们转向DFT的正式定义。

​​

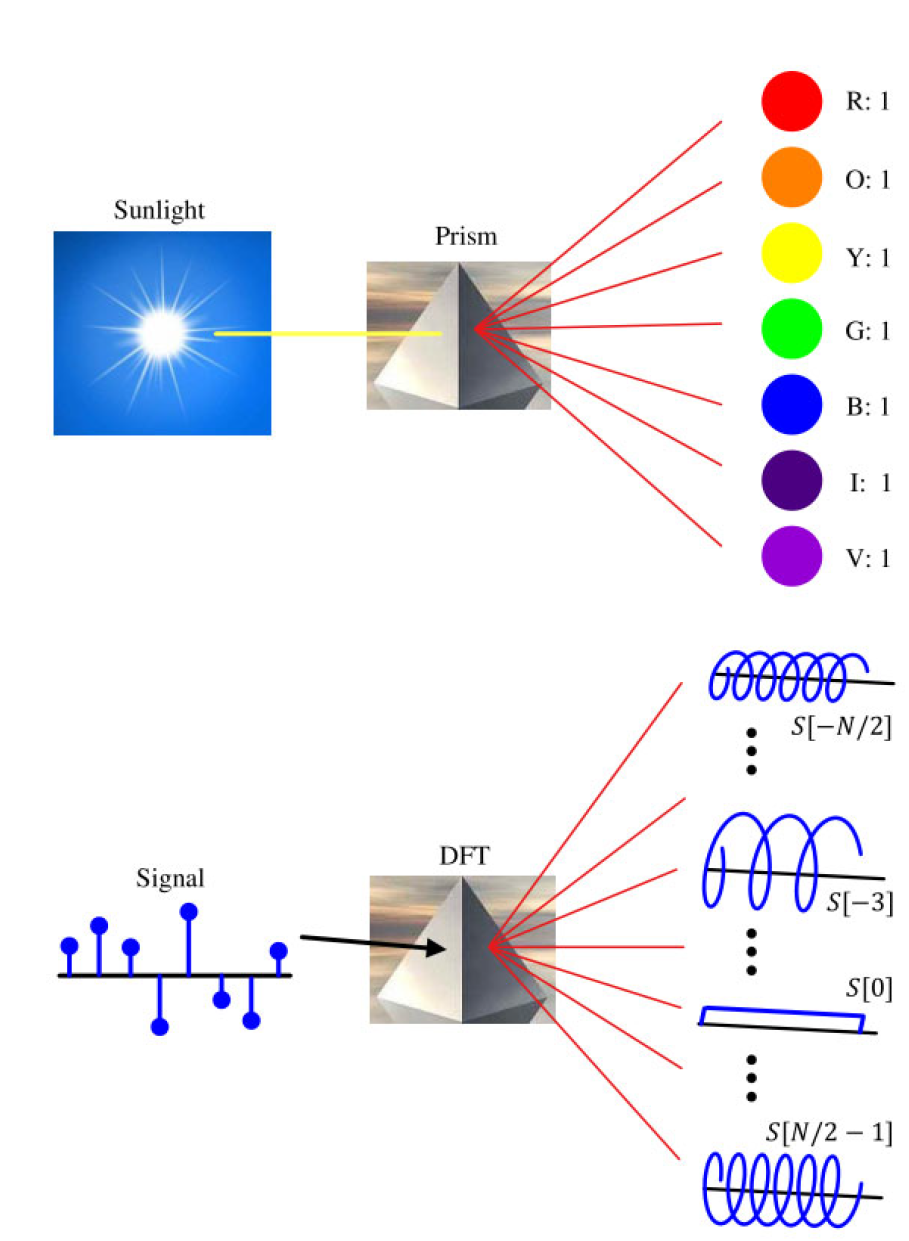
图 1.50：DFT 就像一个棱镜

定义

假设一个离散时间复正弦波被定义为 $V[n]$。

$$\begin{aligned} I &\rightarrow V_I[n] = \cos 2\pi \frac{k}{N} n \\ Q &\uparrow V_Q[n] = \sin 2\pi \frac{k}{N} n \end{aligned}$$

我们实际上想要做的是将一个有限长度信号 $s[n]$ 与 $N$ 个频率为 $k/N$ 的复正弦波（在滞后0的位置上）进行相关运算。根据1.6节的相关性，将 $s[n]$ 与复正弦波 $V^{\ast }[n]$ 逐样相乘并取和。然后，DFT $S[k]$ 由以下公式给出：

$$S[k] = \sum_{n=0}^{N-1} s[n] V^*[n]$$

在 $s[n]$ 的 $I$ 和 $Q$ 分量 $s_I[n]$ 和 $s_Q[n]$ 的形式下，DFT $S[k]$ 可以通过复数的乘法规则求得。

$$\begin{aligned} I &\rightarrow S_I[k] = \sum_{n=0}^{N-1} \left[ s_I[n] \cos 2\pi \frac{k}{N} n + s_Q[n] \sin 2\pi \frac{k}{N} n \right] \\ Q &\uparrow S_Q[k] = \sum_{n=0}^{N-1} \left[ s_Q[n] \cos 2\pi \frac{k}{N} n - s_I[n] \sin 2\pi \frac{k}{N} n \right] \end{aligned} \tag{1.53}$$

对每个 $k$ 来说，在上面的公式中：

• $k$ 是DFT输出在频域中的索引，$k=-N/2,\dots ,-1,0,1,\dots ,N-2,N-1$
• $S[k]$ 是第 $k$ 个DFT输出分量
• $S_I[k]$ 和 $S_Q[k]$ 是DFT $S[k]$ 的 $I$ 和 $Q$ 分量
• $n$ 是输入样本的时间域索引，$n=0,1,\dots ,N-1$
• $s[n]$ 是输入样本序列
• $N$ 是离散时间域中的数据样本数量，也是离散频域中桶的数量

根据定义，DFT的每个输出 $S[k]$ 都是在 $t=0$ 处的输入信号与频率为 $k/N$ 的复正弦波的相关性。由于正交性，与其他所有 $k^{\prime }\ne k$ 的相关性为零，输出仅包含来自频率为 $k/N$ 的复正弦波的信号中的分量。

从另一方面来看，比较与公式 (1.19) 中的相位旋转规则，我们可以观察到 DFT 操作是顺时针旋转信号 $s[n]$。

$$\begin{aligned} I \cdot \cos(\cdot) + Q \cdot \sin(\cdot) \\ Q \cdot \cos(\cdot) - I \cdot \sin(\cdot) \end{aligned}$$

备注 1.10 相关性与正交性的美丽

频率被定义为相位变化的速率。如果 $s[n]$ 包含频率 $+k/N$ 的分量，通过与同一频率但方向相反（即，$-k/N$）的复正弦波逐样旋转，会导致输出为单个数值，这是由于相位相互抵消所致。这个单数自然是频率为 $k/N$ 的复正弦波的光谱幅值，表明了该正弦波在构成 $s[n]$ 中的贡献程度。

这个单数还包含一个常数相位项，因为DFT复正弦波以相位 0 开始，但不是输入信号中的贡献复正弦波。整个过程最终试图找到每个此类复正弦波在所研究信号的构建中的参与度。

信号 $s[n]$ 与其傅里叶变换 $S[k]$ 之间的关系通常表示为：

$$s[n] \xrightarrow{F} S[k]$$

提醒一下，对于采样率 $F_s=30$ kHz 和 64 点 DFT，正弦波的基频为 $F_s\cdot \pm 1/N=\pm 30,000/64=\pm 468.75$ Hz，表示为 $k=\pm 1$。其他分析频率是基频的整数倍，如

• $F_s\cdot \pm 2/N=\pm 937.5$ Hz 表示为 $k=\pm 2$
• $F_s\cdot \pm 3/N=\pm 1406.3$ Hz 表示为 $k=\pm 3$

等等。每个频率代表一个复正弦波，或者等效于两个实正弦波。

由于离散频率轴的周期性，DFT 也可以定义为频率桶 $k=[0,N-1]$。然而，范围 $k=[-N/2,N/2-1]$ 更自然，因为前者对应于我们所认为的一个实正弦波，其构成了一个正频率和一个负频率复正弦波。参见公式 (1.27)。例如，假设在离散频域 $k=5$ 和 $k=-5$ 有两个脉冲，这似乎不传递任何信息。然而，将其视为 $k=5$ 和 $k=-5$ 的两个脉冲立即使人意识到，时间域信号是频率 $F_s\cdot 5/N$ 的一个实正弦波。

逆离散傅里叶变换（iDFT）

正如DFT用于将信号从时域转换到频域，逆离散傅里叶变换（iDFT）用于作为逆过程将信号从频域转换到时域。

iDFT 定义如下：

$$\begin{aligned} I \rightarrow & \quad s_I[n] = \frac{1}{N} \sum_{k=-N/2}^{N/2-1} \left[S_I[k]\cos\left(2\pi \frac{k}{N}n\right) - S_Q[k]\sin\left(2\pi \frac{k}{N}n\right)\right] \\ Q \rightarrow & \quad s_Q[n] = \frac{1}{N} \sum_{k=-N/2}^{N/2-1} \left[S_Q[k]\cos\left(2\pi \frac{k}{N}n\right) + S_I[k]\sin\left(2\pi \frac{k}{N}n\right)\right] \end{aligned} \tag{1.54}$$

请注意，与 DFT 中的求和是关于时间索引 $n$ 不同，iDFT 中的求和是关于频率索引 $k$ 的。此外，与 DFT 相反，复正弦波在此具有逆时针旋转方向，见公式 (1.18) 的相位旋转规则。iDFT 也是一种相关性，就像前面解释的 DFT 一样。幅值缩放为 $1/N$ 以平衡公式 (1.47) 和图 1.46 中正交性定义中产生的因子 $N$。

用文字来说，iDFT 方程比 DFT 方程更容易理解，因为它是基于我们最初的前提，即信号可以表示为适当缩放的复正弦波之和。从 iDFT 的定义可以看出，要重构信号 $s[n]$，我们必须将 $k=-N/2$ 到 $N/2-1$ 的 $N$ 个复正弦波相加，并用 DFT 系数 $S[k]$ 对其加权。这与图 1.35 中所说明的概念相同，当时域信号由许多正弦波构成。唯一的区别在于，在连续时间信号的情况下，这些正弦波的数量可以无限增加。

DFT 的周期性

上述 DFT 方程的一个自然结果是，$S[k]$ 可以被证明为周期为 $N$ 的周期函数。请注意，构成 DFT 输出的复正弦波在 $k$ 中是周期性的，具体如下：

$$\begin{aligned} I \rightarrow & \quad \cos\left(2\pi \frac{k+N}{N} n\right) = \cos\left(2\pi \frac{k}{N} n\right) \\ Q \rightarrow & \quad \sin\left(2\pi \frac{k+N}{N} n\right) = \sin\left(2\pi \frac{k}{N} n\right) \end{aligned}$$

由于离散频率轴本身是周期性的，即频率 $k/N$ 和 $(k+N)/N=k/N+1$ 是相同的，DFT $S[k]$ 与 $S[k+N]$ 相同。因此，

$$S[k+N] = S[k] \tag{1.55}$$

当我们采样一个连续时间信号以获得离散时间信号时，无限的频谱副本以采样率 $F_s$ 的整数倍间隔出现。当我们通过采样频率轴以在 $-0.5F_s$ 到 $+0.5F_s$ 的基带范围内获取 $N$ 个等间隔点时，我们也在隐含地采样这些频谱混叠项，而信号的 DFT 在频域上变得周期性。

注 1.11 DFT 输入是否是周期性的？

有趣的是，使用类似的三角恒等式找到 $S[k+N]$ 可以通过 iDFT 定义（公式 1.54）来实现 $s[n+N]$：

$$s[n + N] = s[n] \tag{1.56}$$

“虽然我们不知道 $s[n]$ 在 $N-1$ 之外发生了什么，但在从 $-N/2$ 到 $N/2-1$ 之间的 $N$ 个离散点采样频率轴时，时域中采样信号的副本在时间域中就像在频域中采样其频谱 $S(F)$ 的副本。”

​​

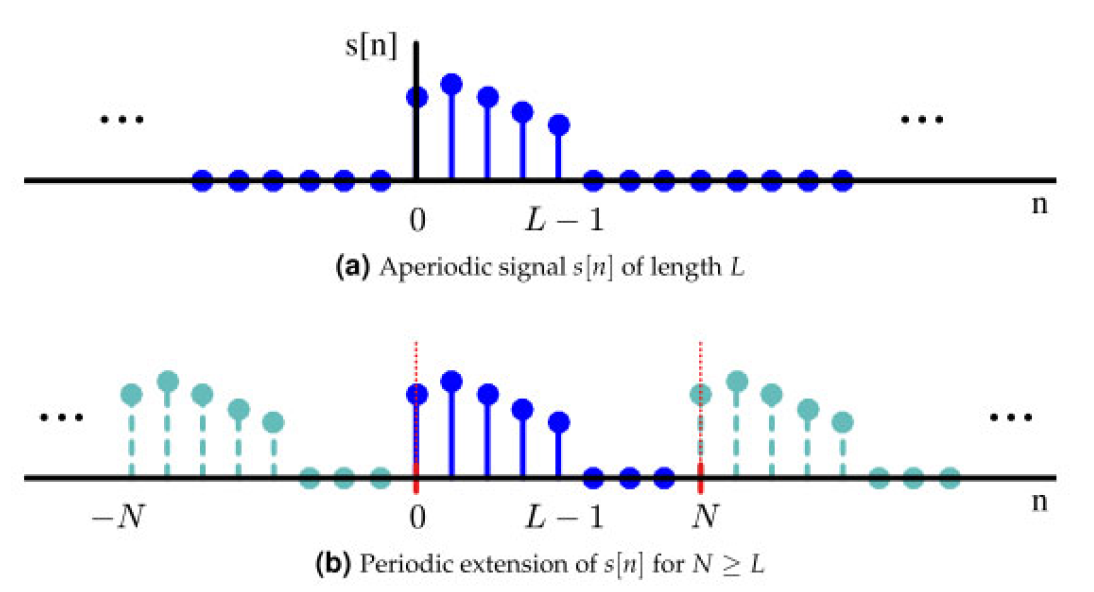
图 1.51：采样频率轴在时域中产生混叠

图 1.51 展示了一个非周期信号 $s[n]$ 及其周期扩展。只要 DFT 长度 $N$ 大于或等于信号长度 $L$，DFT 就能准确地表示输入信号的采样频率响应，没有失真。然而，当 $N<L$ 时，DFT 频谱不再是真实的采样频率域表示，时域中将出现混叠现象。显然，常识也表明对截断输入信号的 DFT（$N<L$）将产生不准确的结果。

这种周期性扩展的一个主要影响是序列移位对 DFT 来说实际上导致循环移位。假设图 1.51 中的 $N=L$。然后，右移 1 个单位将最后一个样本从位置 $n=N-1$ 移出观察窗口 $[0,N-1]$ 到新的位置 $n=N$。此外，它将把第一个样本从其先前在 $n=-1$ 的位置带入观察窗口 $n=0$。概念上，这不仅是窗口 $[0,N-1]$ 内的循环移位，还会在 $0$ 到 $N-1$ 的位置之间引入如图中虚线所示的样本移位。

DFT 对实际频谱的近似

在这个阶段，一个自然的问题是：DFT——一个经过采样的时间域信号的频率函数——在多大程度上近似了底层的傅里叶变换——一个连续时间信号的连续频率函数？最初的猜测是这并不太准确，因为连续傅里叶变换是从负无穷到正无穷的积分，而 DFT 是一个有限和。

实际上，这种近似非常好。然而，这里有两个可能的误差来源。

截断误差：显然，任何没有有限长度的信号 $s[n]$ 必须被截断以适应 DFT 的有限长度。

混叠误差：根据采样定理，采样率必须至少是信号 $s[n]$ 中包含的最大频率的两倍。如果信号不是带限的，就可能会发生混叠。

每个实际信号都占据无限的带宽，因为一个信号不可能同时在时间和频率域中都被限制。为了避免截断误差，信号必须是时间有限的，这使得它的频谱无限，从而导致混叠误差。为了避免混叠误差，信号必须理想地在一个足够高的采样率下是带限的，但这样一个信号不能有有限的持续时间，从而导致截断误差。

对于许多实际的情况，这些误差的量是可以忍受的：对于一个合理的带限信号，这意味着在某个频率范围之外只有非常小的能量，我们可以使信号在时间上有限并用适当的采样率对其进行采样。这使得 DFT 成为分析真实连续时间信号的一个很好的工具。

快速傅里叶变换（FFT）

快速傅里叶变换（FFT）既不是另一种类型的傅里叶变换，也不是DFT的近似。FFT只是利用DFT方程中的冗余性来更快地计算DFT的一种方法。事实上，正是FFT使得傅里叶分析在大多数信号处理应用中成为可能。例如，如果长度为 $N=10^6$ 的信号的FFT在某计算设备上需要1秒钟，那么在相同平台上计算DFT则大约需要28小时！