基础算法练习200题09、水池注水

---

📋前言📋
💝博客：【红目香薰的博客_CSDN博客-计算机理论,2022年蓝桥杯,MySQL领域博主】💝

✍本文由在下【红目香薰】原创，首发于CSDN✍

🤗2022年最大愿望：【服务百万技术人次】🤗

💝专栏地址：【https://blog.csdn.net/feng8403000/category_11958599.html】💝 

---

      为了帮助很多想搞算法但又害怕自己搞不定的孩子们，老师付准备了200个入门的逻辑练习题，在这200个逻辑练习题下可以加强你们的基础算法能力，以次为基础当面对正式的算法题目的时候可以得心应手的面对。 

题目：

甲乙两个水管单独开，注满一池水，分别需要20小时，16小时。丙水管单独开，排一池水要10小时，若水池没水，同时打开甲乙两水管，5小时后，再打开排水管丙，问水池注满还需要多少小时？

题解：

甲功率=1/20(进水)

乙功率=1/16(进水)

丙功率=1/10(排水)

通分一下：

一眼就看出来公分母是80。甲是4/80，乙是5/80，丙是8/80

可以看出，甲乙之和是9/80与丙8/80进行计算。

题目说是先开甲乙5小时，也就是，(9/80)*5，咱们不依然使用80这个分母等于45/80。

只需要计算出剩余的35是如何填充的即可。

已知甲乙之和与丙比较多出1/80。

故而，开启甲乙5小时后打开丙排水，需要时间35小时即可。

编码分析1：

我这里不使用欧几里得定理，咱们一步步分析。

没有通分，使用浮点数记性计算，最终出现浮点数计算错误，无法精准答案。

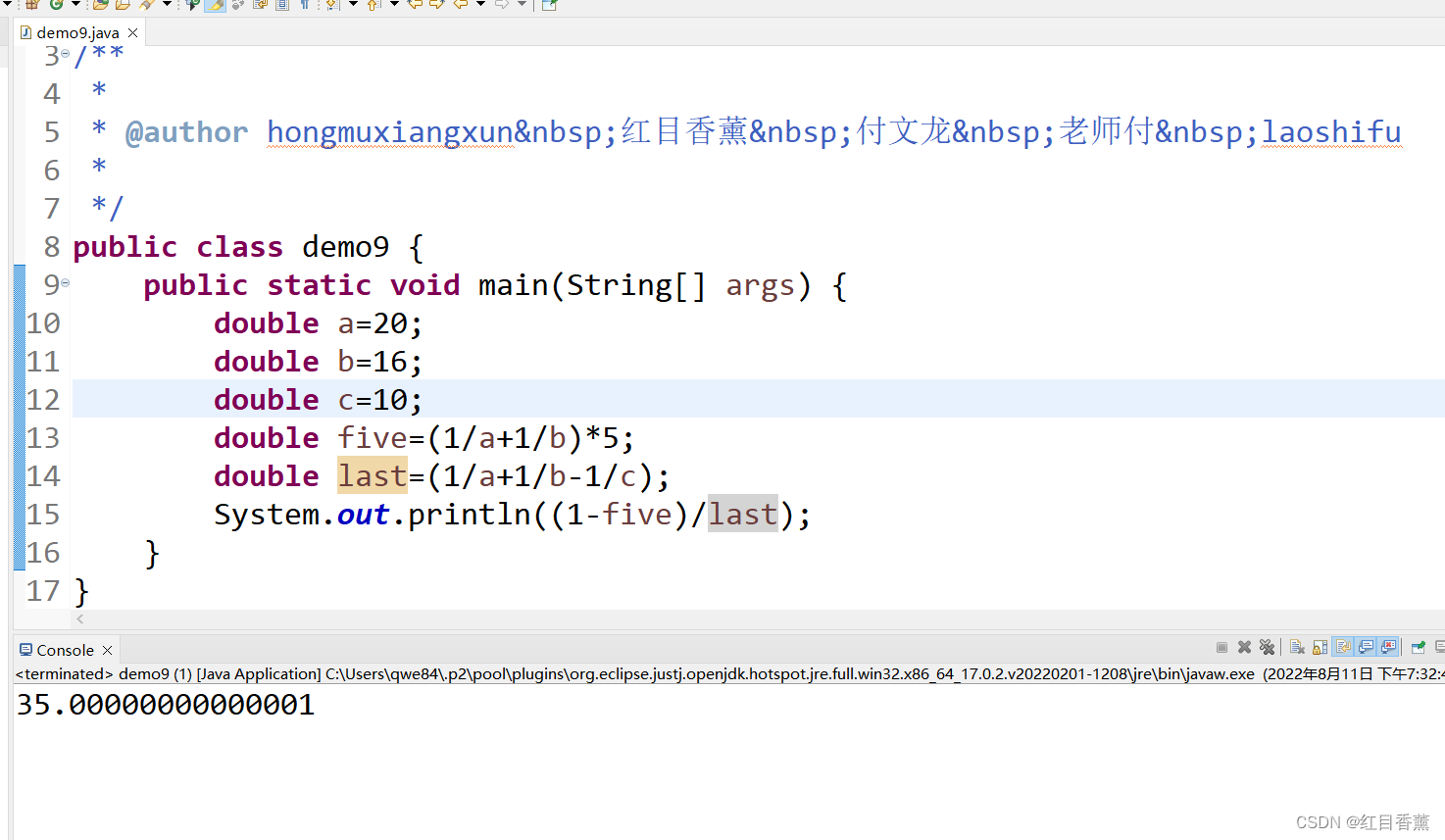
由于答案肯定是整数，所以最后取整即可。

package com.item.action;

/**
 * 
 * @author hongmuxiangxun 红目香薰 付文龙 老师付 laoshifu
 *
 */
public class demo9 {
	public static void main(String[] args) {
		double a=20;
		double b=16;
		double c=10;
		double five=(1/a+1/b)*5;
		double last=(1/a+1/b-1/c);
		double result=(1-five)/last;
		System.out.println(String.format("%.0f", result));
	}
}

编码分析2：(算法升级，难度提升到40题附近，可以先略过，后面也会有对欧几里得定理的具体拆分式讲解)

这个题需要一定的数学基础，起码会通分。

样例：

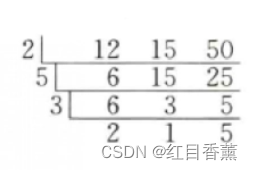
最小公分母=2*5*3*2*1*5=300

那么，20与16页一样

也可以：

20=2*2*5

16=2*2*2*2

都是质因数，那个数量多选按个，相乘即可。

最小公倍数=2*2*2*2*5=80

这里套用欧几里得定理直接出结果：

package com.item.action;

/**
 * 
 * @author hongmuxiangxun 红目香薰 付文龙 老师付 laoshifu
 *
 */
public class demo9_1 {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		System.out.println("最大公约数："+gcd(2, 16));
		System.out.println("最小公倍数："+lcm(20, 16));
	}

	/**
	 * 
	 * 最大公约数
	 * @param x
	 * @param y
	 * @return
	 */
	public static int gcd(int x, int y) {
		if (y == 0) {
			return x;
		}
		return gcd(y,x%y);
	}
	/**
	 * 最小公倍数·此写法对于比较大的数处理较好
	 * @param x
	 * @param y
	 * @return
	 */
	public static int lcm(int x, int y) {
		int gcd = gcd(x, y);
		return (x / gcd) * (y / gcd) * gcd;
	}

}

取整计算可以消除浮点数运算丢失精度的问题：

package com.item.action;

/**
 * 
 * @author hongmuxiangxun 红目香薰 付文龙 老师付 laoshifu
 *
 */
public class demo9_1 {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		//通分后的最小公倍数就可以当做水池的总单位：lcm
		int lcm = lcm(20, 16);
		//计算前5小时总水量
		int five=(lcm/20+lcm/16)*5;
		//剩余水池空间lcm-five
		int last=lcm-five;
		//计算5小时后的功率
		int power=lcm/20+lcm/16-lcm/10;
		//剩余空间/功率=最后消耗时间
		int result=last/power;
		System.out.println(result);
	}

	/**
	 * 
	 * 最大公约数
	 * @param x
	 * @param y
	 * @return
	 */
	public static int gcd(int x, int y) {
		if (y == 0) {
			return x;
		}
		return gcd(y,x%y);
	}
	/**
	 * 最小公倍数·此写法对于比较大的数处理较好
	 * @param x
	 * @param y
	 * @return
	 */
	public static int lcm(int x, int y) {
		int gcd = gcd(x, y);
		return (x / gcd) * (y / gcd) * gcd;
	}

}