深度学习中的优化算法

      深度学习中的优化算法，是模型训练期间微调神经网络参数的关键元素。其主要作用是最小化模型的误差或损失，从而提高性能。各种优化算法(称为优化器)采用不同的策略来收敛到最佳参数值，从而有效地提高预测效果。

      在深度学习的背景下，优化是指调整模型参数以最小化(或最大化)某些目标函数(objective function)或成本函数(cost function)的过程，即找到目标函数的最小值或最大值。目标函数通常是衡量模型在某项任务上表现如何的指标，例如最小化一组训练数据上的误差(error)。该过程涉及找到导致模型最佳性能的最佳参数集。深度学习中使用各种优化算法来寻找最佳参数集。这些算法负责在训练过程中迭代更新模型参数。在深度学习中，目标函数代表误差或损失。

      优化算法主要分为两类：一阶优化算法(First-Order Optimization Algorithms)和二阶优化算法(Second-Order Optimization Algorithms)。一阶优化技术易于计算且耗时较少，在大型数据集上收敛速度非常快。仅当二阶导数已知时，二阶技术才会更快，否则，这些方法在时间和内存方面总是更慢且计算成本高昂。

      一阶优化算法：使用相对于参数的梯度值来最小化或最大化损失函数。最广泛使用的一阶优化算法是梯度下降。梯度下降旨在找到成本函数或损失函数的最小值。此函数表示模型的预测值与训练数据集中的实际值之间的差异。一阶导数告诉我们函数在某个特定点是减少还是增加。一阶导数基本上给我们一条与其误差曲面上某点相切的线(First order Derivative basically give us a line which is Tangential to a point on its Error Surface)。

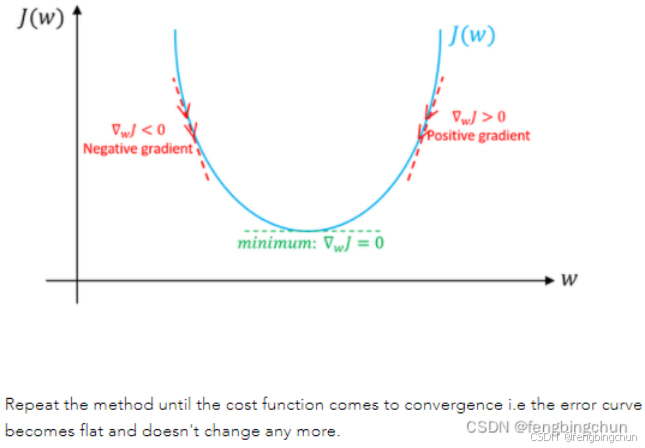
      下图图解说明：假设只有weight没有bias。如果weight(w)的特定值的斜率>0，则表示我们在最优w*的右侧，在这种情况下，更新将是负数，并且w将开始接近最优w*。但是，如果weight(w)的特定值的斜率<0，则更新将为正值，并将当前值增加到w以收敛到w*的最佳值。重复该方法，直到成本函数收敛。

      1.批量梯度下降(Batch Gradient Descent)：找到最小值，控制方差，然后更新模型的参数，最终让我们收敛。梯度下降主要用于在神经网络模型中进行权重更新，即在某个方向上更新和调整模型的参数，以便我们可以最小化损失函数。batch size为整个训练样本集数量。

      2.Mini-Batch梯度下降：小批量梯度下降，如batch size为32，远小于整个训练样本集数量。

      3.随机梯度下降(Stochastic Gradient Descent, SGD)：batch size为1，使用单个训练样本进行模型更新。

      4.Mini-Batch随机梯度下降：结合了批量梯度下降和随机梯度下降的优点。

      5.基于动量的随机梯度下降(Momentum-based SGD)：有助于在相关方向上加速SGD收敛并抑制震荡的方法。

      6.Nesterov加速梯度下降(Nesterov Accelerate Gradient Descent, NAG)：在基于Momentum SGD的基础上作了改动。

      7.具有自适应学习率的梯度下降(Gradient Descent with Adaptive Learning Rate, AdaGrad)：针对数据集中的不同特征采用自适应学习率。在迭代过程中不断调整学习率；提高SGD的鲁棒性；收敛速度较慢。

      8.AdaDelta：是AdaGrad的扩展，改善AdaGrad的两个主要缺点：在整个训练过程中，学习率的持续衰减以及需要手动选择学习率的需求。

      9.均方根传播(Root Mean Square Propagation, RMSprop)：对AdaGrad进行改进，为了解决AdaGrad急剧下降的学习率问题。

      10.自适应矩估计(Adaptive Moment Estimation, Adam)：结合了动量梯度下降(在平缓区域移动更快)和RMSProp梯度下降(调整学习率)的优势。使用最广泛的优化算法之一。

      11.AdaMax：基于无穷范数的Adam的变体。

      12.Nadam(Nesterov-accelerated adaptive moment estimation)：用Nesterov的加速梯度修改了Adam的动量组成部分，是Adam和NAG两种算法的结合。

      13.AMSGrad：Adam算法的一种改进。

      二阶优化算法：使用二阶导数(也称为Hessian)来最小化或最大化损失函数。Hessian是二阶偏导数矩阵。由于二阶导数计算成本高，因此二阶不常用。二阶导数告诉我们一阶导数是增加还是减少，这暗示了函数的曲率。二阶导数为我们提供了一个与误差曲面曲率相切的二次曲面(Second-Order Derivative provide us with a quadratic surface that touches the curvature of the Error Surface)。如牛顿法。

      每个优化器都有其独特的优点和缺点，最佳选择取决于特定的深度学习任务和数据集的特征。优化器的选择会极大地影响训练过程中收敛的速度和质量，最终影响深度学习模型的最终性能。

      (1).批量梯度下降：优点：简单且容易实现。缺点：在大数据集上计算成本高昂；可能会陷入局部最小值。可在小数据集上使用。

      (2).SGD：优点：速度快；能处理大数据集。缺点：更新频繁可能导致不稳定。可在大数据集上使用。

      (3).小批量梯度下降：优点：平衡效率与稳定性；更具通用性的更新。缺点：需要调整batch size。可用于大多数深度学习任务。

      (4).AdaGrad：优点：调整每个参数的学习率；适用于稀疏数据。缺点：学习率可以减小到零，从而停止学习。可用于稀疏数据集。

      (5).RMSprop：优点：解决AdaGrad学习率降低问题；根据最近的梯度调整学习率。缺点：在非凸问题上仍然会陷入局部最小值。可用于非凸优化问题。

      (6).AdaDelta：优点：无需设置默认学习率；解决学习率降低问题。缺点：比RMSprop和AdaGrad更复杂。

      (7).Adam：优点：结合了AdaGrad和RMSprop的优点；自适应学习率。缺点：需要调整超参(尽管使用默认值通常效果很好)。可在大多数深度学习中应用。

      注：以上整理的内容主要来自:

      1. https://medium.com

      2. https://arxiv.org/pdf/2007.14166

      PyTorch中优化算法的实现在：torch/optim目录，支持的优化算法包括：Adafactor、Adadelta、Adagrad、Adam、Adamax、AdamW、ASGD、LBFGS、NAdam、RAdam、RMSprop、Rprop、SGD、SparseAdam。

      GitHub：https://github.com/fengbingchun/NN_Test