原帖地址:http://blog.csdn.net/maverick1990/article/details/13291679
生成学习算法
本次课程大纲:
1、 生成学习算法
2、 高斯判别分析(GDA,Gaussian Discriminant Analysis)
- 高斯分布(简要)
- 对比生成学习算法&判别学习算法(简要)
3、 朴素贝叶斯
4、 Laplace平滑
复习:
分类算法:给出一个训练集,若使用logistic回归算法,其工作方式是观察这组数据,尝试找到一条直线将图中不同的类分开,如下图。
之前讲的都是判别学习算法,本课介绍一种不同的算法:生成学习算法。
1、 生成学习算法
例:对恶性肿瘤和良性肿瘤的分类
除了寻找一个将两类数据区分的直线外,还可以用如下方法:
1) 遍历训练集,找到所有恶性肿瘤样本,直接对恶性肿瘤的特征建模;同理,对良性肿瘤建模。
2) 对一个新的样本分类时,即有一个新的病人时,要判断其是恶性还是良性,用该样本分别匹配恶性肿瘤模型和良性肿瘤模型,看哪个模型匹配的更好,预测属于恶性还是良性。
这种方法就是生成学习算法。
两种学习算法的定义:
1) 判别学习算法:
- 直接学习p(y|x),即给定输入特征,输出所属的类
- 或学习得到一个假设hθ(x),直接输出0或1
2) 生成学习算法:
- 对p(x|y)进行建模,p(x|y)表示在给定所属的类的情况下,显示某种特征的概率。处于技术上的考虑,也会对p(y)进行建模。
- p(x|y)中的x表示一个生成模型对样本特征建立概率模型,y表示在给定样本所属类的条件下
例:在上例中,假定一个肿瘤情况y为恶性和良性,生成模型会对该条件下的肿瘤症状x的概率分布进行建模
- 对p(x|y)和p(y)建模后,根据贝叶斯公式p(y|x) = p(xy)/p(x) = p(x|y)p(y)/p(x),可以计算:p(y=1|x) = p(x|y=1)p(y=1)/p(x),其中,p(x) = p(x|y=0)p(y=0) + p(x|y=1)p(y=1)
2、 高斯判别分析GDA
GDA是一种生成学习算法。
GDA的假设条件:
1) 假设输入特征x∈Rn,并且是连续值。
2) 假设p(x|y)满足高斯分布
*高斯分布基础知识:
设随机变量z满足多元高斯分布,z~N(μ,∑),均值向量为μ,协方差矩阵为∑。
其概率密度函数为:
多元高斯分布为一元高斯分布的推广,也是钟形曲线,z是一个高维向量。
多元高斯分布注意两个参数即可:
- 均值向量μ
- 协方差矩阵∑= E[(Z-E[Z])(Z-E[Z])T]=E[(x-μ)(x-μ)T]
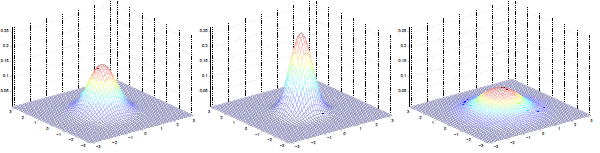
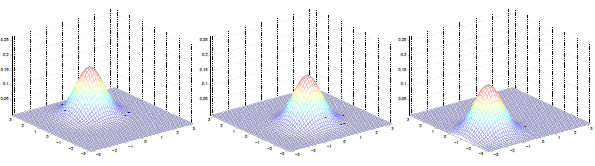
多元高斯分布图:
左图:μ=0,∑=I(单位矩阵)
中图:μ=0,∑=0.6I,图形变陡峭
右图:μ=0,∑=2I,图形变扁平
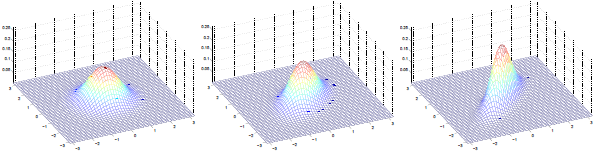
三图中μ=0,∑如下:
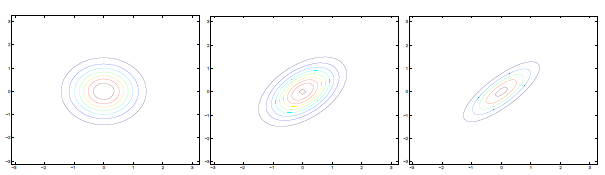
可见增加矩阵对角元素的值,即变量间增加相关性,高斯曲面会沿z1=z2(两个水平轴)方向趋于扁平。其水平面投影图如下:
即增加∑对角线的元素,图形会沿45°角,偏转成一个椭圆形状。
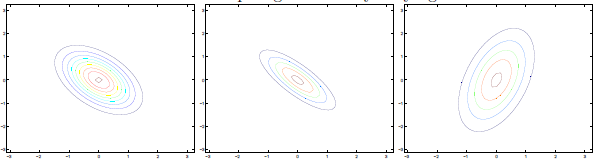
若∑对角线元素为负,图形如下:
∑分别为:
不同μ的图形如下:
μ分别为:
μ决定分布曲线中心的位置。
GDA拟合:
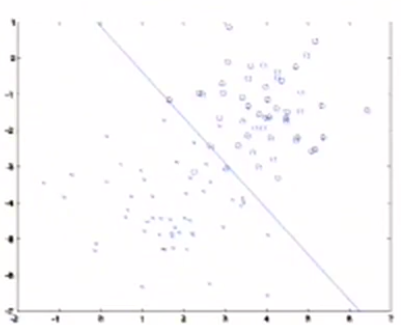
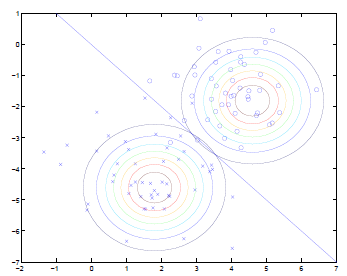
给出训练样本如下图所示:
- 观察正样本(图中的x),拟合正样本的高斯分布,如图中左下方的圆,表示p(x|y=1)
- 观察负样本(图中的圈),拟合负样本的高斯分布,如图中右上方的圆,表示p(x|y=0)
- 通过这两个高斯分布的密度函数,定义出两个类别的分隔器,即图中的直线
- 这条分隔器直线比之前的logistic拟合的直线要复杂
GDA模型:
写出其概率分布:
参数包括φ,μ0,μ1,∑,对数似然性为:
由于第一个等式为xy的联合概率,将这个模型命名为联合似然性(Joint likelihood)。
*对比logistic回归中的对数似然性:
由于计算的是y在x条件下的概率,将此模型命名为条件似然性(conditional likelihood)
通过对上面对数似然性求极大似然估计,参数的结果为:
φ:训练样本中标签为1的样本所占的比例
μ0:分母为标签为0的样本数,分子是对标签为0的样本的x(i)求和,结合起来就是对对标签为0的样本的x(i)求均值,与高斯分布参数μ为均值的意义相符
μ1:与μ0同理,标签改为1
GDA预测:
预测结果应该是给定x的情况下最可能的y,等式左边的运算符argmax表示计算p(y|x)最大时的y值,预测公式如下:
因为p(x)独立于y,所以可以忽略p(x)。
*如果p(y)为均匀分布,即每种类型的概率都相同,那么也可以忽略p(y),要求的就是使p(x|y)最大的那个y。不过这种情况并不常见。
GDA和logistic回归的联系:
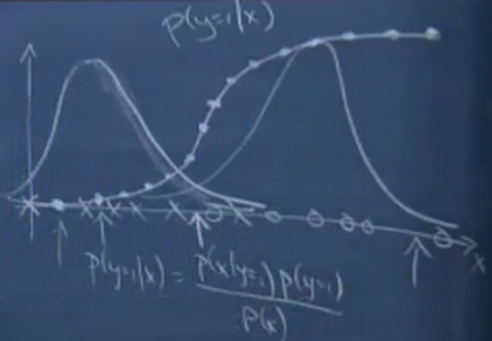
例:假设有一个一维训练集,包含一些正样本和负样本,如下图x轴的叉和圈,设叉为0,圈为1,用GDA对两类样本分别拟合高斯概率密度函数p(x|y=0)和p(x|y=1),如下图的两个钟形曲线。沿x轴遍历样本,在x轴上方画出其相应的p(y=1|x)。
如选x轴靠左的点,那么它属于1的概率几乎为0,p(y=1|x)=0,两条钟形曲线交点处,属于0或1的概率相同,p(y=1|x)=0.5,x轴靠右的点,输出1的概率几乎为1,p(y=1|x)=1。最终发现,得到的曲线和sigmoid函数曲线很相似。
简单来讲,就是当使用GDA模型时,p(x|y)属于高斯分布,计算p(y|x)时,几乎能得到和logistic回归中使用的sigmoid函数一样的函数。但实际上还是存在本质区别的。
使用生成学习算法的优缺点:
给出两个推论:
推论1:
x|y 服从高斯分布 => p(y=1|x)是logistic函数
该推论在反方向不成立。
推论2:
x|y=1 ~ Poisson(λ1),x|y=0 ~ Poisson(λ0) => p(y=1|x)是logistic函数
x|y=1 ~ Poisson(λ1)表示x|y=1服从参数为λ1泊松分布
推论3:
x|y=1 ~ ExpFamily(η1),x|y=0 ~ ExpFamily (η0) => p(y=1|x)是logistic函数
推论2的推广,即x|y的分布属于指数分布族,均可推出结论。显示了logistic回归在建模假设选择方面的鲁棒性。
优点:
推论1反方向不成立,因为x|y服从高斯分布这个假设更强,GDA模型做出了一个更强的假设,所以,若x|y服从或近似服从高斯分布,那么GDA会比logistic回归更好,因为它利用了更多关于数据的信息,即算法知道数据服从高斯分布。
缺点:
如果不确定x|y的分布情况,那么判别算法logistic回归性能更好。例如,预先假设数据服从高斯分布,但是实际上数据服从泊松分布,根据推论2,logistic回归仍能获得不错的效果。
生成学习算法比判决学习算法需要更少的数据。如GDA的假设较强,所以用较少的数据能拟合出不错的模型。而logistic回归的假设较弱,对模型的假设更为健壮,拟合数据需要更多的样本。
3、 朴素贝叶斯
另一种生成学习算法。
例:垃圾邮件分类
实现一个垃圾邮件分类器,以邮件输入流作为输入,确定邮件是否为垃圾邮件。输出y为{0,1},1为垃圾邮件,0为非垃圾邮件。
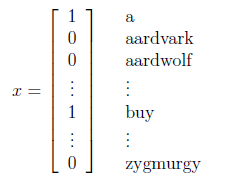
首先,要将邮件文本表示为一个输入向量x,设已知一个含有n个词的字典,那么向量x的第i个元素{0,1}表示字典中的第i个词是否出现在邮件中,x示例如下:
要对p(x|y)建模,x是一个n维的{0,1}向量,假设n=50000,那么x有2^50000种可能的值,一种方法是用多项式分布进行建模(伯努利分布对01建模,多项式分布对k个结果建模),这样就需要2^50000-1个参数,可见参数过多,下面介绍朴素贝叶斯的方法。
假设xi在给定y的时候是条件独立的,则x在给定y下的概率可简化为:
这个假设直观理解为,已知一封邮件是不是垃圾邮件(y),以及一些词是否出现在邮件中,这些并不会帮助你预测其他的词是否出现在邮件中。虽然这个假设不是完全正确的,但是朴素贝叶斯依然应用于对邮件进行分类,对网页进行分类等用途。
*对于朴素贝叶斯,我的理解为:通过指定一些垃圾邮件的关键词来计算某个邮件是垃圾邮件的概率。具体讲,就是给定字典后,给出每个词的p(xi|y=1),即这个词xi在垃圾邮件中出现的概率,然后对于一个邮件,将邮件所有词的p(xi|y)的相乘,就是邮件为垃圾邮件的概率。再简化一些,规定p(xi|y=1)={0,1},即划定一些关键词,这些关键词在邮件中出现的概率就是这封邮件为垃圾邮件的概率。
模型参数包括:
Φi|y=1 = p(xi=1|y=1)
Φi|y=0 = p(xi=1|y=0)
Φy = p(y=1)
联合似然性:
求得参数结果:
Φi|y=1的分子为标记为1的邮件中出现词j的邮件数目和,分母为垃圾邮件数,总体意义就是训练集中出现词j的垃圾邮件在垃圾邮件中的比例。
Φi|y=0就是出现词j的非垃圾邮件在非垃圾邮件中的比例。
Φy就是垃圾邮件在所有邮件中的比例。
求出上述参数,就知道了p(x|y)和p(y),用伯努利分布对p(y)建模,用上式中p(xi|y)的乘积对p(x|y)建模,通过贝叶斯公式就可求得p(y|x)
*实际操作中,例如将最近两个月的邮件都标记上“垃圾”或“非垃圾”,然后得到(x(1),y(1))…(x(m),y(m)),x(i)为词向量,标记出现在第i个邮件中的词,y(i)为第i个邮件是否是垃圾邮件。用邮件中的所有出现的词构造字典,或者选择出现次数k次以上的词构造字典。
朴素贝叶斯的问题:
设有一封新邮件中出现一个字典没有的新词,设其标号为30000,因为这个词在垃圾邮件和非垃圾邮件中都不存在,则p(x3000|y=1)=0,p(x30000|y=0)=0,计算p(y=1|x)如下:
p(y=1|x) = p(x|y=1)p(y=1) / ( p(x|y=1)p(y=1) + p(x|y=0)p(y=0))
由于p(x|y=1)=p(x|y=0)=0(p(x30000|y=1)=p(x30000|y=0)=0,则乘积为0),则p(y=1|x)=0/0,则结果是未定义的。
其问题在于,统计上认为p(x30000|y)=0是不合理的。即在过去两个月邮件里未出现过这个词,就认为其出现概率为0,并不合理。
概括来讲,即之前没有见过的事件,就认为这些事件不会发生,是不合理的。通过Laplace平滑解决这个问题。
4、 Laplace平滑
根据极大似然估计,p(y=1) = #”1”s / (#”0”s + #”1”s),即y为1的概率是样本中1的数目在所有样本中的比例。Laplace平滑就是将分子分母的每一项都加1,,即:
p(y=1) = (#”1”s+1) / (#”0”s+1 + #”1”s+1)
例:给出一支球队5场比赛的结果作为样本,5场比赛都输了,记为0,那么要预测第六场比赛的胜率,按照朴素贝叶斯为:p(y=1) = 0/(5+0) = 0,即样本中没有胜场,则胜率为0,显然这是不合理的。按照Laplace平滑处理,p(y=1) = 0+1/(5+1+0+1) = 1/7,并不为0,且随着负场次的增加,p(y=1)会一直减小,但不会为0。
更一般的,若y取k中可能的值,比如尝试估计多项式分布的参数,得到下式:
即值为j的样本所占比例,对其用Laplace平滑如下式:
对于朴素贝叶斯,得到的结果为:
在分子上加1,分母上加2,解决了0概率的问题








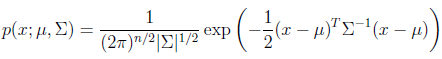
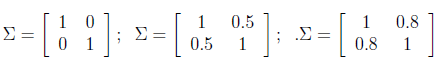
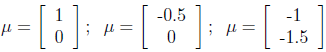
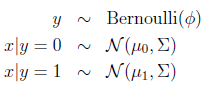
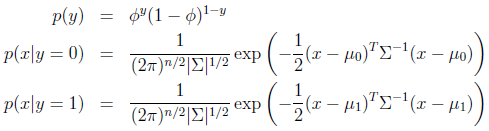
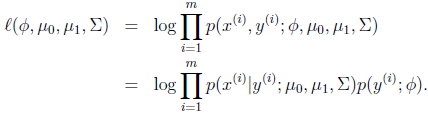
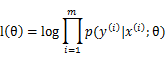
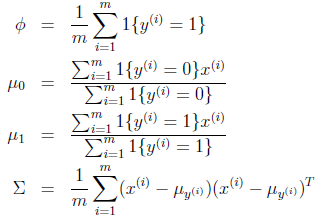
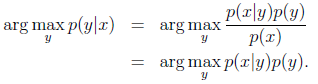
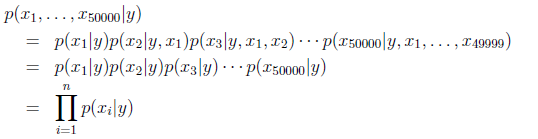
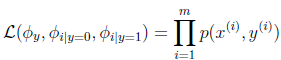
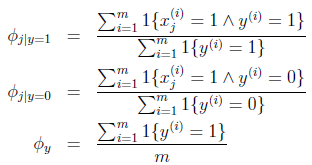
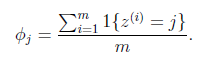
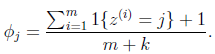
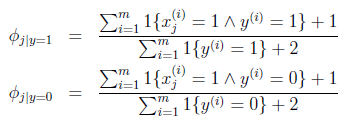














 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








