巧解螺旋矩阵

😎 作者介绍：我是程序员行者孙，一个热爱分享技术的制能工人。计算机本硕，人工制能研究生。公众号：AI Sun，视频号：AI-行者Sun
🎈 本文专栏：本文收录于《深入浅出算法》系列专栏，相信一份耕耘一份收获，我会系统全面的分享算法课程，届时可以拳打字节，脚踢腾讯
🤓 欢迎大家关注其他专栏，我将分享Web前后端开发、人工智能、机器学习、深度学习从0到1系列文章。
🖥 随时欢迎您跟我沟通，一起交流，一起成长、进步！

先贴上我的图（击败100%的西佳佳选手），各位朋友往下看（我的是法二）~

题目描述：

给你一个 m 行 n 列的矩阵 matrix ，请按照 顺时针螺旋顺序 ，返回矩阵中的所有元素。

示例 1：

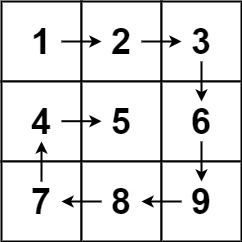
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,2,3,6,9,8,7,4,5]

示例 2：

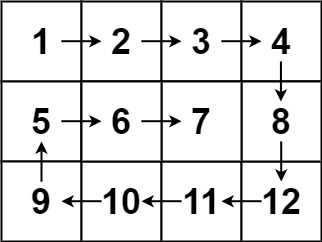
输入：matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出：[1,2,3,4,8,12,11,10,9,5,6,7]

思路一：常见的思路，就是模拟他的这个过程，按照访问过程去访问每一个元素。可以模拟螺旋矩阵的路径。初始位置是矩阵的左上角，初始方向是向右，当路径超出界限或者进入之前访问过的位置时，顺时针旋转，进入下一个方向。

判断路径是否进入之前访问过的位置需要使用一个与输入矩阵大小相同的辅助矩阵 visited，其中的每个元素表示该位置是否被访问过。当一个元素被访问时，将 visited 中的对应位置的元素设为已访问。

class Solution {
private:
    // 定义四个方向：右、下、左、上
    static constexpr int directions[4][2] = {{0, 1}, {1, 0}, {0, -1}, {-1, 0}};
public:
    // 螺旋顺序遍历矩阵
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        if (matrix.size() == 0 || matrix[0].size() == 0) {
            return {}; // 如果矩阵为空，返回空向量
        }

        int rows = matrix.size(), columns = matrix[0].size();
        vector<vector<bool>> visited(rows, vector<bool>(columns));
        int total = rows * columns;
        vector<int> order(total);

        int row = 0, column = 0;
        int directionIndex = 0;
        for (int i = 0; i < total; i++) {
            order[i] = matrix[row][column];
            visited[row][column] = true;
            int nextRow = row + directions[directionIndex][0], nextColumn = column + directions[directionIndex][1];
            if (nextRow < 0 || nextRow >= rows || nextColumn < 0 || nextColumn >= columns || visited[nextRow][nextColumn]) {
                directionIndex = (directionIndex + 1) % 4;
            }
            row += directions[directionIndex][0];
            column += directions[directionIndex][1];
        }
        return order;
    }
};

思路二：我们每次循环还得看边界，判断是否被访问过，这也太麻烦了，那我们修改边界，使得没访问过的元素在边界内不就好了

• 首先设定上下左右边界
• 其次向右移动到最右，此时第一行因为已经使用过了，可以将其从图中删去，体现在代码中就是重新定义上边界
• 判断若重新定义后，上下边界交错，表明螺旋矩阵遍历结束，跳出循环，返回答案
• 若上下边界不交错，则遍历还未结束，接着向下向左向上移动，操作过程与第一，二步同理
• 不断循环以上步骤，直到某两条边界交错，跳出循环，返回答案

代码一和代码二思想相同，写法不一致，时空复杂度不可兼得（看读者喜欢哪种了）~

代码一（时间上超越100%）：

class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        vector<int> res; // 存放结果的数组
        if(matrix.empty()) return res; // 如果矩阵为空，直接返回结果数组
        
        int len_l = 0, len_r = matrix[0].size() - 1; // 左右边界的索引
        int high_l = 0, high_r = matrix.size() - 1; // 上下边界的索引
        
        while(true) { // 循环直到遍历完整个矩阵
            // 从左到右遍历顶部行
            for(int i = len_l; i <= len_r; i++)
                res.push_back(matrix[high_l][i]);
            high_l++; // 上边界向下移动
            
            // 检查是否遍历完所有行
            if(high_l > high_r) break;
            
            // 从上到下遍历右侧列
            for(int i = high_l; i <= high_r; i++)
                res.push_back(matrix[i][len_r]);
            len_r--; // 右边界向左移动
            
            // 检查是否遍历完所有列
            if(len_l > len_r) break;
            
            // 从右到左遍历底部行
            for(int i = len_r; i >= len_l; i--)
                res.push_back(matrix[high_r][i]);
            high_r--; // 下边界向上移动
            
            // 检查是否遍历完所有行
            if(high_l > high_r) break;
            
            // 从下到上遍历左侧列
            for(int i = high_r; i >= high_l; i--)
                res.push_back(matrix[i][len_l]);
            len_l++; // 左边界向右移动
            
            // 检查是否遍历完所有列
            if(len_l > len_r) break;
        }
        return res; // 返回结果数组
    }
};

代码二（内存上超越80%）： 

class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        vector<int> res;
        // 如果矩阵为空，直接返回空向量
        if(matrix.empty()) return res;
        
        int left = 0, right = matrix[0].size() - 1;
        int top = 0, bottom = matrix.size() - 1;
        
        while(left <= right && top <= bottom) {
            // 从左到右遍历顶部行
            for(int i = left; i <= right; i++)
                res.push_back(matrix[top][i]);
            top++;
            
            // 从上到下遍历右侧列
            for(int i = top; i <= bottom; i++)
                res.push_back(matrix[i][right]);
            right--;
            
            // 如果还存在下一行
            if(top <= bottom) {
                // 从右到左遍历底部行
                for(int i = right; i >= left; i--)
                    res.push_back(matrix[bottom][i]);
                bottom--;
            }
            
            // 如果还存在左侧列
            if(left <= right) {
                // 从下到上遍历左侧列
                for(int i = bottom; i >= top; i--)
                    res.push_back(matrix[i][left]);
                left++;
            }
        }
        return res;
    }
};