本文主要整理一下机器学习中的范数规则化学习的内容:
- 规则化
-什么是规则化
-为什么要规则化
-规则化的理解
-怎么规则化
-规则化的作用 - 范数
-L0范数和L1范数
-L2范数
-L1范数和L2范数 - 补充
-condition number
-微博、知乎部分讨论 - 参考附录
规则化
什么是规则化?
回顾一下机器学习算法的3个要点:1.根据数据找合适的模型;2.定义损失以评估模型;3.设计求解优化的方法。
再回顾一下监督学习:规则化参数(防止模型过分拟合训练数据)的同时最小化误差(模型拟合训练数据的偏差)。
Regularization, in mathematics and statistics and particularly in the fields of machine learning and inverse problems, refers to a process of introducing additional information in order to solve an ill-posed problem or to prevent overfitting. —— from wikipedia
Regularization是引入额外的信息来解决ill-posed问题或者防止overfitting的过程。
规则化的表现形式: ω∗=argminω∑iL(yi,f(xi;ω))+λΩ(ω)
第一项是衡量模型对样本的预测与真实的误差(二者越接近越好),最小化误差指该部分。
第二项是对参数w的规则化函数Ω(w)约束模型(使模型简单)。最小化模型测试误差指该部分。
为什么要规则化?
为了解决ill-posed问题或者防止overfitting,期望获得一个能够很好地解释数据而且simple的模型,或者从统计角度来说,是找一个减少过度拟合的估计方法。
一般从线性回归问题也称最小二乘问题(Least Squares Problem, LSP)和逻辑回归问题(Logistic Regression Problem, LRP)引入。前者想象预测的变量是数字,后者预测的变量是“是/否”的这种分类答案。这两个问题中会出现下面的情况导致overfitting:
- When the number of observations or training examples m is not large enough compared to the number of feature variables n, over-fitting may occur. 样本数量m选不如特征维度n大
- Tends to occur when large weights are found in x. 待预测的向量x的有过大的权重,也就是拟合函数的系数过大【考虑太过全面,把noise 或者 error in the data都考虑进去了,过分拟合。这样导致拟合函数波动大。同一量级上考虑,系数小曲线偏平滑,系数大,曲线偏陡峭】
针对1.解决方法是:
- 减少特征数量
- 可以人工选择重要的特征变量以减少特征数。
- 自动的,特征选择(Feature Selection) -> 稀疏性 -> 正则化
-增加样本数量
针对2.解决方法是:
- 正则化
当然还有其他的方法,本文不介绍了。eg.cross-validation, early stopping, pruning, Bayesian priors on parameters or model comparison
规则化的理解
让模型简单,意味着要采取措施降低模型复杂度(过多参数导致模型复杂–稀疏 is ok),使用规则项来约束模型(约束了待学习的模型参数w,也就变相约束了模型)的特性。
还有几种种理解角度:
角度一
经验风险=平均损失函数 ,结构风险=损失函数+正则化项(惩罚项)
正则化是结构风险最小化的策略。正则化项一般是模型复杂度的单调递增函数,模型越复杂,正则化值就越大。比如,模型参数向量的范数。角度二
正则化项的引入其实是利用了先验知识,体现了人对问题的解的认知程度或者对解的估计。这样就可以将人对该问题的理解和需求(先验知识)融入到模型的学习当中,对模型参数设置先验,强行地让学习到的模型具有人想要的特性,例如稀疏、低秩、平滑等等。(正则与稀疏、低秩和平滑的关系)
L1正则是laplace先验,l2是高斯先验,分别由参数sigma确定。角度三
附录的Sparsity and the Lasso
最小二乘问题中,ranx(A)<样本数量。对要解决的问题加限制条件(角度二中的先验)–>[subject to]
图像表示出来是这样的:
利用对偶,KKT等转化成这样:为什么要凸的,这就用着了。
本质上都差不多,切入点不同,就可以从不同方面理解了。
怎么规则化?
前面提到,正则化项一般是模型复杂度的单调递增函数,模型越复杂,正则化值就越大(为了给予复杂模型以惩罚,因为优化的时候要最小化函数,想要得到simple模型,越复杂,惩罚越大),并且优化过程还想得到稀疏的参数。(看怎么理解稀疏了,L1参数大多为0,L2参数大多接近0)。下面介绍的是用向量范数的形式来规则化,看范数那一节。
为什么参数要稀疏呢?——特征选择;问题的可解释性
1. 特征选择:large-scale 可能大部分特征是对于最终的输出y是无影响的或者影响很小的。训练时最小化目标函数,如果考虑这些特征会得到更小的误差,但是会对新样本的预测结果产生影响。Lasso regularization的引入是为了完成特征自动选择,它会在优化过程中主动去学习去掉这些没有用的特征,把特征对应的权重置为0。【L1】
2. 可解释性:例如一回归问题,假设回归模型为:y=w1*x1+w2*x2+…+w1000*x1000+b。通过学习,如果最后学习到的w*,只有很少的非零元素,大部分w*为0或接近于0,例如只有5个非零的wi,那可以认为y只受这5个xi(因素)的影响,更有利于人们对问题的认识和分析,抓住影响问题的主要方面(因素)更符合认知习惯。【L2】
【正则与平滑】实际上,这些参数值越小,通常对应于越光滑的函数,也就是更加简单的函数。
【正则与稀疏】为什么正则化会使参数稀疏呢?
规则化的作用?
- 防止过拟合(平衡了偏差与方差,拟合能力与泛化能力,结构风险和经验风险);
- 正则化导致的稀疏性是有益的:特征选择以及把人对于问题的认知作为先验引入优化过程中;
- 降低condition number,处理因其过大导致逆矩阵不好求的情况;
范数
L0范数和L1范数
L0范数是指向量中非0的元素的个数。
L1范数是指向量中各个元素绝对值之和,也称Lasso regularization
如果用L0范数来规则化一个参数矩阵W的话,就是希望W的大部分元素都是0,也就是让参数W是稀疏的。L0应该不算是norm。像L1,L2等可以转换到convex或者本身就是convex的这种算norm。(能用来优化)
为什么L1范数会使权值稀疏?
见L1范数和L2范数部分。
L2范数
∥x∥2 权值衰减 weight decay , 回归问题里叫岭回归(ridege regression)
指向量各元素的平方和再求平方根。让L2范数的规则项最小,可以使得W的每个元素都很小,都接近于0,但与L1范数不同,它不会让它等于0,而是接近于0。
L2范数好处
1.学习理论角度——L2范数可以防止过拟合,提升模型的泛化能力
2.优化计算角度——L2范数有助于处理 矩阵 condition number不好的情况下矩阵求逆很困难的问题
为什么L2范数有助于处理矩阵condition number不好的情况下矩阵求逆很困难的问题?
以最小二乘问题LSP为例,添加正则项(add “preference” for certain parameter values)之后的cost function J :
用同样的方法,求得新的解的表达式为








 本文详细介绍了机器学习中的规则化(正则化)及其作用,包括防止过拟合和降低模型复杂度。重点探讨了L0、L1和L2范数的概念,以及它们在模型简化和参数稀疏性上的差异。L1范数常导致稀疏解,适合特征选择,而L2范数则通过权重衰减防止过拟合,保持模型平滑。文章还讨论了正则化的理解、应用及矩阵条件数对数值稳定性的影响。
本文详细介绍了机器学习中的规则化(正则化)及其作用,包括防止过拟合和降低模型复杂度。重点探讨了L0、L1和L2范数的概念,以及它们在模型简化和参数稀疏性上的差异。L1范数常导致稀疏解,适合特征选择,而L2范数则通过权重衰减防止过拟合,保持模型平滑。文章还讨论了正则化的理解、应用及矩阵条件数对数值稳定性的影响。
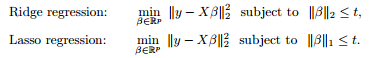

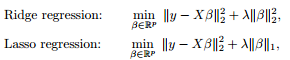
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章















 877
877

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








